斯坦福大學機器學習——高斯判別分析

轉自 http://blog.csdn.net/linkin1005/article/details/39054023

同樸素貝葉斯一樣，高斯判別分析（Gaussian discriminant analysismodel, GDA）也是一種生成學習算法，在該模型中，我們假設y給定的情況下，x服從混合正態分布。通過訓練確定參數，新樣本通過已建立的模型計算出隸屬不同類的概率，選取概率最大為樣本所屬的類。

一、混合正態分布（multivariate normal distribution）

混合正態分布也稱混合高斯分布。該分布的期望和協方差為多元的：期望,協方差，協方差具有對稱性和正定性。混合高斯分布：，它的的概率密度函數為：

其中，為混合高斯分布的期望，為其協方差，表示協方差的行列式。

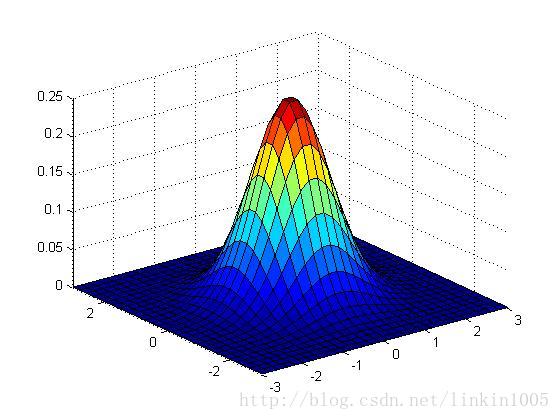
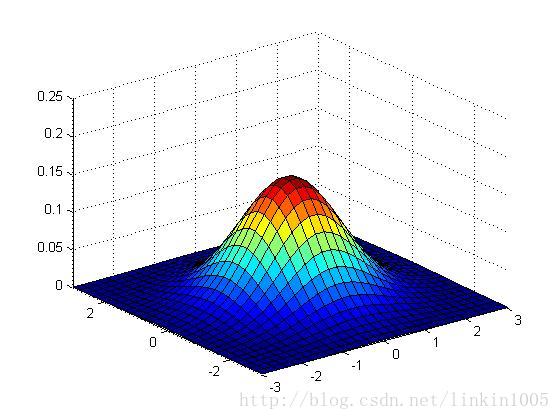
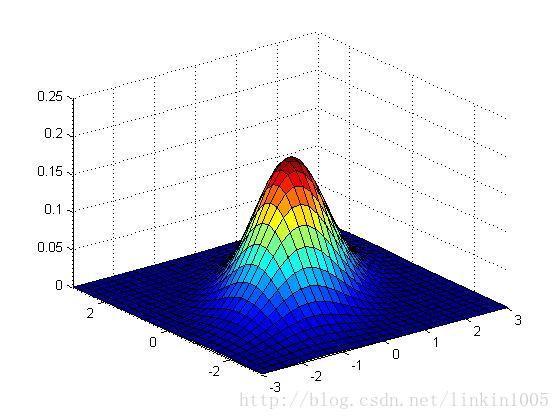
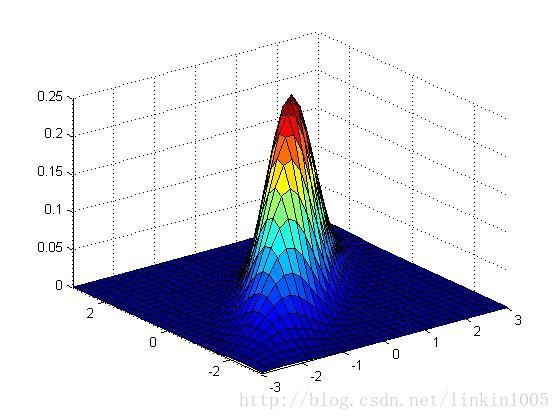
下面用圖形直觀的看一下二維高斯分布的性質：

以上三個圖形的期望都為：，最左端圖形的協方差，中間的，最右端的，我們可以看出：當變小時，圖像變得更加“瘦長”，而當增大時，圖像變得更加“扁平”。

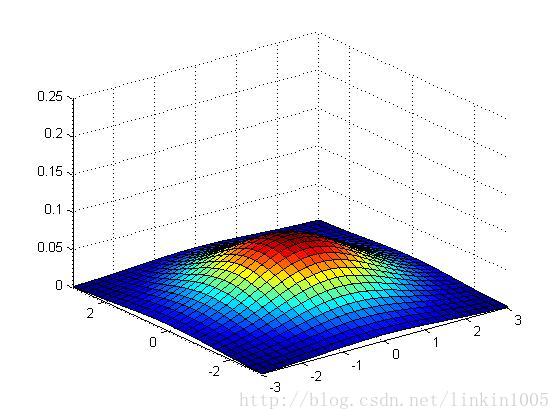
再看看更多的例子：

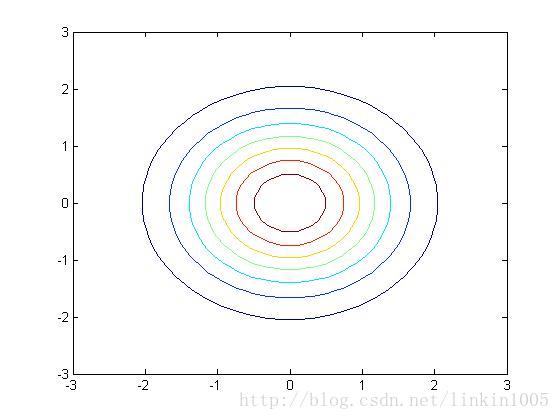
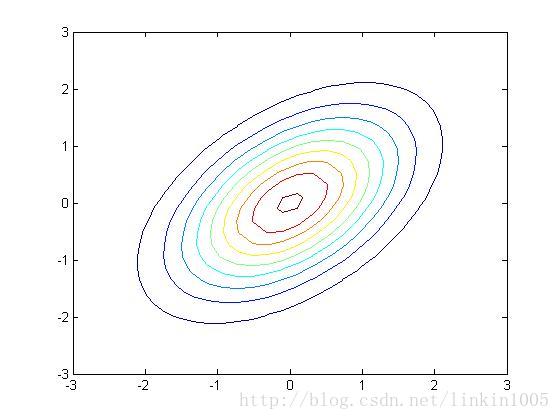
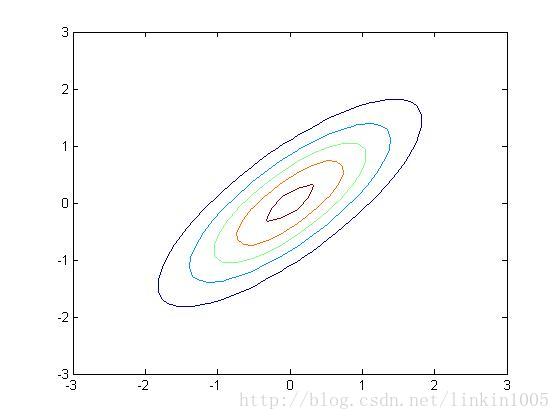
以上三個圖形的期望都為：，從左至右三個圖形的協方差分別的：

可以看到隨著矩陣的逆對角線數值增加，圖形延方向，即底部坐標45度角壓縮。圖形在這個方向更加“扁”。

以上三幅圖分別是以上圖形的等高線，可以更直觀的看到調整逆對角線的數值對圖像的壓縮程度。

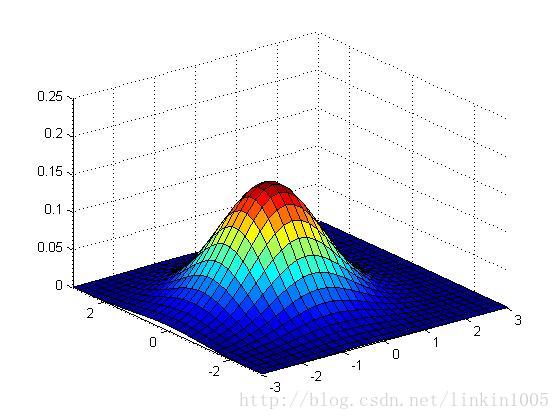
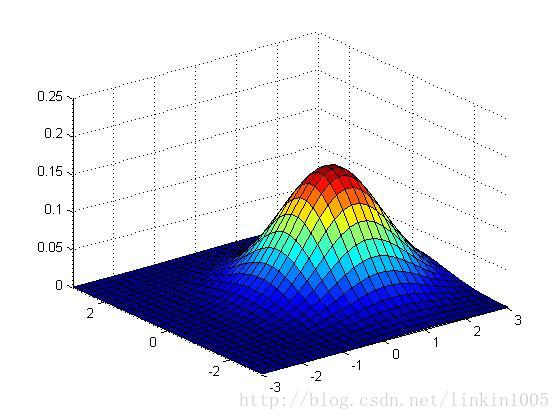
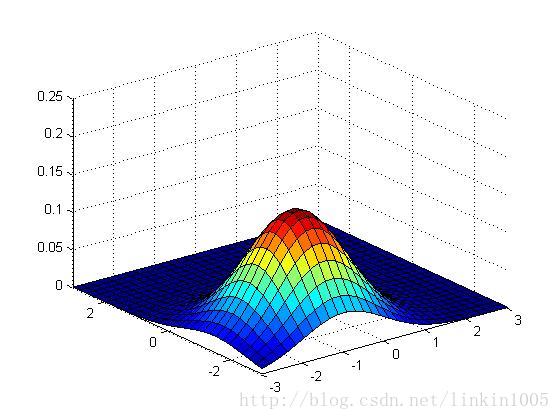
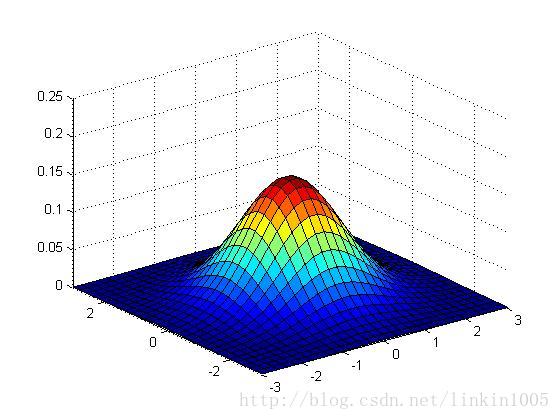
以上三幅圖保持協方差不變，期望的值分別為

；；

可以看出，隨著期望的改變，圖形在平面上平移，而其他特性保持不變。

二、高斯判別分析模型

如果特征值x是連續的隨機變量，我們可以使用高斯判別分析模型完成特征值的分類。為了簡化模型，假設特征值為二分類，分類結果服從0-1分布。（如果為多分類，分類結果就服從二項分布）

模型基于這樣的假設：

他們的概率（密度）函數分別為：

模型的待估計參數為，通常模型有兩個不同的期望，而有一個相同的協方差。

該模型的極大似然對數方程為：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??

求解該極大似然方程得：

在對計算完成之后，將新的樣本x帶入進建立好的模型中，計算出、，選取概率更大的結果為正確的分類。

三、GDA和logistic回歸

GDA模型和logistic回歸模型存在這樣有趣的關系：假如我們將視作關于x的函數，該函數可以表示成logistic回歸形式：

?

其中，可以用以為變量的函數表示。

前文中已經提到，如果為混合高斯分布，那么，就可以表示成logistic回歸函數形式；相反，如果可表示成logistic回歸函數形式，并不代表服從混合高斯分布。這意味著GDA比logistic回歸需要更加嚴格的模型假設，當然，如果混合高斯模型的假設是正確的，那么，GDA具有更高的擬合度。基于以上原因，在實踐中使用logistic回歸比使用GDA更普遍。