拾取模型的原理及其在THREE.JS中的代碼實現

?

1.?Three.js中的拾取?

?

?

?

1.1.?從模型轉到屏幕上的過程說開

?

??由于圖形顯示的基本單位是三角形，那就先從一個三角形從世界坐標轉到屏幕坐標說起，例如三角形abc

?

?

?

?

?

?

?

?

?

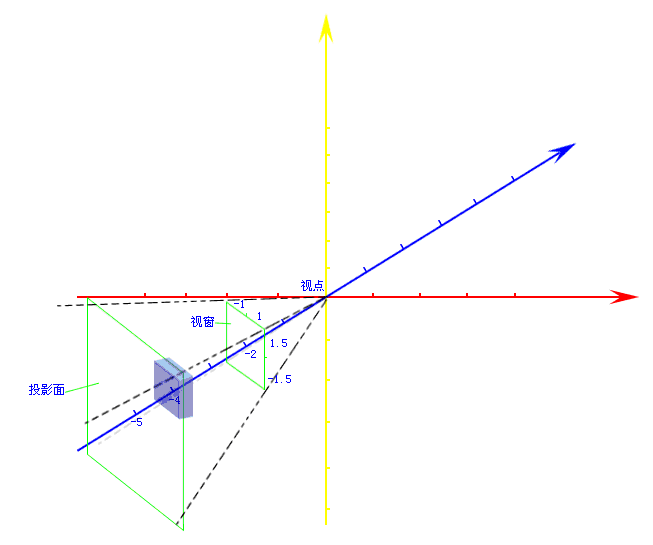
乘以模型視圖矩陣就進入了視點坐標系，其實就是相機所在的坐標系，如下圖：

?

?

?

進入視點坐標系后，再乘以投影矩陣，就會變換到一個立方體內，如下圖:

?

?

?

這個時候整個三角形就位于中心位于坐標系原點，邊長為2的立方體內，在這個立方體內，三角形要計算光照，要裁剪，然后乘以視口矩陣，最后轉到屏幕上。

?

?

?

?

?

轉到屏幕上后，三角形的所有點的Z坐標就是深度坐標，一定在(0, 1)這個區間內，那么哪些點的Z坐標是0呢，在投影坐標系中，一定是投影視景體的前剪切平面上的點，而投影視景體的后剪切平面上的點的Z坐標就是1。

?

1.2.?思路來了

?

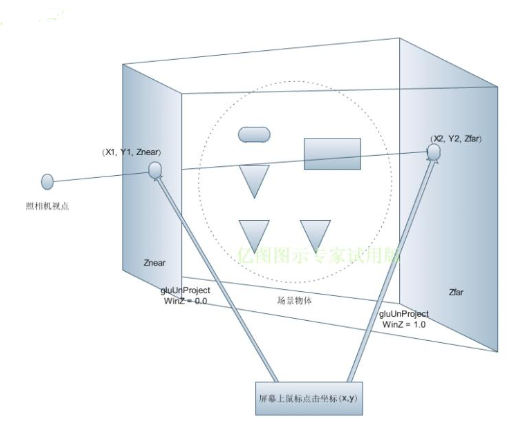
???根據以上三角形轉換到屏幕坐標上的過程可以分析出，鼠標在屏幕上點擊的時候，可以得到二維坐標p(x, y),再加上深度坐標的范圍(0, 1), 就可以形成兩個三位坐標A(x, y, 0), B(x, y, 1), ?由于它們的Z軸坐標是0和1，則轉變到投影坐標系的話，一定分別是前剪切平面上的點和后剪切平面上的點，也就是說，在投影坐標系中，A點一定在能看見的所有模型的最前面，B點一定在能看見的所有的模型的最后邊，假設視口矩陣的逆矩幀，投影矩陣的逆矩陣，模型視圖矩陣的逆矩陣為M, N, P，則?P * N * M * A = A1, ?P * N * M * B = B1, 在世界坐標系中，點A1B1就可以形成一個射線,此射線和模型再求交，就能選中模型。如下圖是在視點坐標系中的情形。注意，求交可以在視點坐標系或者世界坐標系計算都可以，但一般會在世界坐標坐標系中計算。

?

?

?

1.3.?拾取的優化，射線和AABB包圍盒求交

?

????如果射線和所有的模型求交，顯然不是一個好辦法，一般情況下會進行一些優化，比如先和模型的包圍盒求交，如果和模型的包圍盒不相交的話，就放過去，否則就接著往下進行，和模型的所有三角面片求交。

?

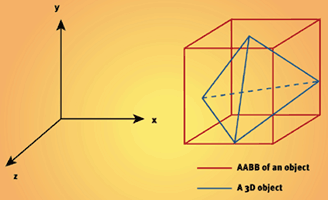
??????那么什么是包圍盒呢？在計算機圖形學與計算幾何領域，一組物體的包圍體就是將物體組合完全包容起來的一個封閉空間。將復雜物體封裝在簡單的包圍體中，就可以提高幾何運算的效率。通常簡單的物體比較容易檢查相互之間的重疊。其中有一種包圍盒叫做AABB,?AABB的全稱是axis aligned bounding box，就是我們常常提到軸向包圍盒，這個盒子的邊是平行于x/y/z軸的。?所有的2d和3d物體都是由點組成的，所以只要找出這些物體的最大值點和最小值點，那么就可以使用這兩個點表示該物體的AABB包圍盒了。
? ? ? ?檢測碰撞的時候我們只需要檢測這些物體的AABB（即他們的最大值點和最小值點）是否相交，就可以判斷是否碰撞了。

?

?

?

?

?

?

?

1.4.?射線和三角形相交

?

?????判斷射線和包圍盒是否求交后，就輪到判斷是否和三角形求交了，最先想到的是 首先判斷射線是否與三角形所在的平面相交，如果相交，再判斷交點是否在三角形內。判斷射線是否與平面相交, 判斷點是否在三角形內.

?

1.5.?THREE.JS中求交的代碼實現

?

??three.js中的一個案例，名字叫webgl_interactive_lines.html,可以選中一根線，并顯示一個小球。根據以上的思路，代碼注釋如下：

?

//鼠標點擊的屏幕坐標轉換到視點坐標系

?

var vector = new THREE.Vector3( mouse.x, mouse.y, 1 ).unproject( camera );

?

?//在視點坐標系中形成射線

?

?raycaster.set( camera.position,vector.sub( camera.position ).normalize() );

?

?//射線和模型求交，選中一系列直線

?

var intersects = raycaster.intersectObjects( parentTransform.children, true);

?

if ( intersects.length > 0 ) {

?

if ( currentIntersected !== undefined )

?

?{

?

?currentIntersected.material.linewidth = 1;

?

?}

?

???//第一個直線

?

currentIntersected = intersects[ 0 ].object;

?

currentIntersected.material.linewidth = 5;

?

????//把球設為可見，并且位置移到鼠標點擊的屏幕位置

?

sphereInter.visible = true;

?

????sphereInter.position.copy( intersects[ 0 ].point );

?

}

?

歡迎加微信 nuonuodi_1, 交流更多的技術問題

?