眾所周知，二維碼通常是黑白的，而且是由若干個長方形或正方形小塊平鋪而成。但從人們的審美角度來看，常見的黑白二維碼不免讓人審美疲勞。本文試著從分塊上色的角度對二維碼進行美化，并嘗試講一下“美化”的編程思路。

一、緣由及目的：

首先，我們來看看正常情況下的黑白二維碼，如圖1：

圖1? 普通二維碼（黑白條塊）

上色的難點在于如何上色，上什么色，也就是哪些塊“著”什么顏色。（關于彩色二維碼的效果，請參考我的另一篇文章：《C#彩色藝術化二維碼樣式設計（僅說思路）》http://blog.csdn.net/johnsuna/article/details/7933619）

如果上錯了色，也會成為“大花臉”，變得并不藝術。就好像漂亮的農村姑娘，如果穿上大花衣裳，看上去鮮艷，但仍然顯示不出其天生的麗質，反而顯得“很土”。如下圖2及圖3：

?

圖2? ?大花臉式的彩色二維碼

圖3? 單塊隨機色（彩色）二維碼

而上色的難點在于分塊，也就是將二維碼分成多少塊、如何分塊，相關色塊上什么顏色，后一個問題是美術工程師考慮的，不在本文討論范圍之內。從圖1，圖2來看，分塊的歸類并不容易或者說我們從外觀上還不好判斷哪些塊分在一起成為一個大色塊。

經過上面圖3、下面圖4的圓角化處理后，色塊的劃分是顯而易見的。具體如何圓角化處理，請見我的另一篇文章《C#彩色藝術化二維碼樣式設計（僅說思路）》http://blog.csdn.net/johnsuna/article/details/7933619?及http://blog.csdn.net/johnsuna/article/details/7948907。

圖4? 圓角化藝術二維碼（黑白色）

為了闡述方便，我將圖1的關鍵塊進行了編號，如下圖5所示：

圖5?? 對圖1黑白二維碼相關關鍵色塊進行編號

與圖5相對應，圖6為圓角化分塊后的帶編號的圖片：

圖6???對圖2的關鍵塊進行編號

下圖7為們我要的最終效果：

圖7? 最終需要的效果示意

盡管我的上色功夫（美感）不怎么樣，但總體效果比圖1-圖4的效果確實好多了。

二、算法研究：

如下圖8所示，為了方便講述，我將圖7中色塊7、8、9、10、11中的每個單元格又按a,b,c……進行了編號并給每個單元格加了一個黑邊框。

圖8? 單元格

圖8中，單元格7a和7b最終組成一個豎條色塊，單元格8為一個獨立的色塊，9a與9b組成一個橫條色塊，而10a,10b...f 又組成一個L形的色塊。如圖7所示，12-18等由多個單元格彼此相連而組成一個大的色塊，其中，編號為16的色塊面積最大。

接下來，重點研究算法。

首先必須找到分塊的“點”，觀察圖7和圖8，我們經過對比可以發現，分隔各塊之間的交接點有一個共同的規律：交接點外圍相鄰對角均為空。

具體地說，就是：以“交接點”為中心的3*3個單元格區域（含交接點本身）內，如果該交接點的外圍8個點中，有兩個斜角（不管是呈現“/”或“\”，也不管是哪一個角位，如左上或右下，或左下或右上）的點均為空白，那么，此點必為分塊關鍵點，也就是“交接點”。

經過觀察和研究，還有一種辦法，那就是“廣度優先遍歷”。如下圖：

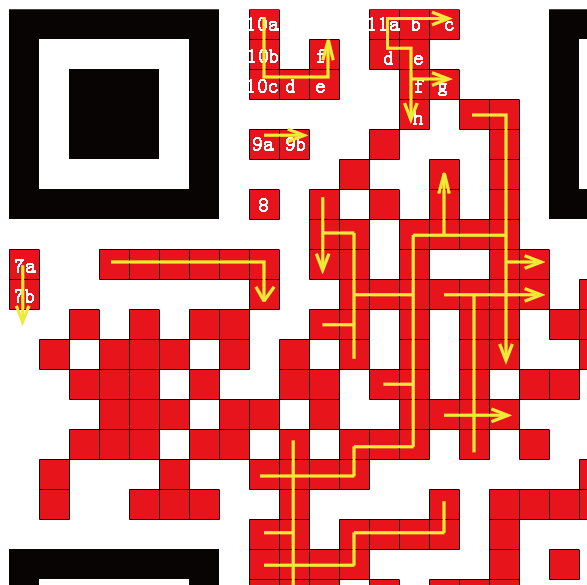
圖9? 單點水平/垂直延伸法示意

此算法也是棋牌或連連看等游戲常用的算法了。網上有很多類似的例子，就不再詳解。另外，此算法可以與分形遞歸算法相結合，實現快速有效地對整個圖像的分塊上色。