四元素的真面目..........簡單粗暴

作者：Yang Eninala
鏈接：https://www.zhihu.com/question/23005815/answer/33971127
來源：知乎
著作權歸作者所有。商業轉載請聯系作者獲得授權，非商業轉載請注明出處。
?

根據我的理解，大多數人用漢密爾頓四元數就只是做三維空間的旋轉變換（我反正沒見過其他用法）。那么你不用學群論，甚至不用復習線性代數，看我下面的幾張圖就可以了。

首先，定義一個你需要做的旋轉。旋轉軸為向量 $v=(vx,vy,vz)$ ，旋轉角度為 $\theta$ （右手法則的旋轉）。如下圖所示：
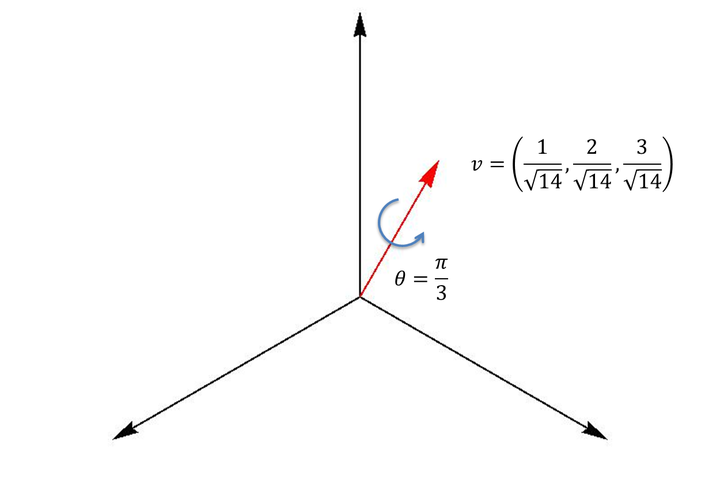
此圖中 $v=(\frac{1}{\sqrt{14} } ,\frac{2}{\sqrt{14} } ,\frac{3}{\sqrt{14} })$ , $\theta =\frac{\pi }{3}$

那么與此相對應的四元數（下三行式子都是一個意思，只是不同的表達形式）
$q=(cos(\frac{\theta }{2} ),sin(\frac{\theta }{2} )*vx,sin(\frac{\theta }{2} )*vy,sin(\frac{\theta }{2} )*vz)$
$q=(cos(\frac{\pi }{6} ),sin(\frac{\pi }{6} )*\frac{1}{\sqrt{14} } ,sin(\frac{\pi }{6} )*\frac{2}{\sqrt{14} },sin(\frac{\pi }{6} )*\frac{3}{\sqrt{14} })$
$q=cos(\frac{\pi }{6} )+sin(\frac{\pi }{6} )*\frac{1}{\sqrt{14} }i +sin(\frac{\pi }{6} )*\frac{2}{\sqrt{14} }j+sin(\frac{\pi }{6} )*\frac{3}{\sqrt{14} }k$

這時它的共軛（下三行式子都是一個意思，只是不同的表達形式），
$q^{-1} =(cos(\frac{\theta }{2} ),-sin(\frac{\theta }{2} )*vx,-sin(\frac{\theta }{2} )*vy,-sin(\frac{\theta }{2} )*vz)$
$q^{-1} =(cos(\frac{\pi }{6} ),-sin(\frac{\pi }{6} )*\frac{1}{\sqrt{14} } ,-sin(\frac{\pi }{6} )*\frac{2}{\sqrt{14} },-sin(\frac{\pi }{6} )*\frac{3}{\sqrt{14} })$
$q^{-1} =cos(\frac{\pi }{6} )-sin(\frac{\pi }{6} )*\frac{1}{\sqrt{14} }i -sin(\frac{\pi }{6} )*\frac{2}{\sqrt{14} }j-sin(\frac{\pi }{6} )*\frac{3}{\sqrt{14} }k$

如果你想算一個點 $w=(wx,wy,wz)$ 在這個旋轉下新的坐標 $w^{'}$ ,需要進行如下操作，
1.定義純四元數
$qw=(0,wx,wy,wz)=0+wx*i+wy*j+wz*k$
2.進行四元數運算
$qw^{'} =q*qw*q^{-1}$
3.產生的 $qw^{'}$ 一定是純四元數，也就是說它的第一項為0，有如下形式：
$qw^{'} =(0,wx^{'},wy^{'},wz^{'})=0+wx^{'}*i+wy^{'}*j+wz^{'}*k$
4. $qw^{'}$ 中的后三項 $(wx^{'},wy^{'},wz^{'})$ 就是 $w^{'}$ ：
$w^{'} =(wx^{'},wy^{'},wz^{'})$
這樣，就完成了一次四元數旋轉運算。

同理，如果你有一個四元數：
$q=(q1,q2,q3,q4)=(cos(\frac{\theta }{2} ),sin(\frac{\theta }{2} )*vx,sin(\frac{\theta }{2} )*vy,sin(\frac{\theta }{2} )*vz)$
那么，它對應一個以向量 $v=(vx,vy,vz)$ 為軸旋轉 $\theta$ 角度的旋轉操作（右手法則的旋轉）。

***********************************************************************************************************
如果你想對四元數有著更深入的了解，請往下看。

四元數由漢密爾頓發明，這一發明起源于十九世紀的某一天。在這一天早上，漢密爾頓下樓吃早飯。這時他的兒子問他，“爸爸，我們能夠對三元數組（triplet，可以理解為三維向量）做乘法運算么？”漢密爾頓說“不行，我只能加減它們。”

這時來自21世紀的旁白旁先生說，“大家快來看十九世紀的數學家有多二，連內積和外積都不是知道。”

十九世紀的漢密爾頓也許確實不知道內積和外積，但是他知道，他想要的三維向量乘法要比內積和外積運算“高大上”很多。這一乘法運算要滿足下列四條性質：
1.運算產生的結果也要是三維向量
2.存在一個元運算，任何三維向量進行元運算的結果就是其本身
3.對于任何一個運算，都存在一個逆運算，這兩個運算的積是元運算
4.運算滿足結合律

換而言之，漢密爾頓想定義的不是一個簡單的映射關系，而是一個群！（后來我們知道四元數所在群為S3，而四元數所代表的三維旋轉是SO(3)，前者是后者的兩倍覆蓋）內積連性質1都不滿足，外積不滿足性質3。

漢密爾頓先生就這么被自己兒子提出的問題難倒了。經歷了無數個日日夜夜，他絞盡腦汁也沒想明白這個問題。終于有一天（1843年的一天），漢密爾頓先生終于意識到了，自己所需要的運算在三維空間中是不可能實現的，但在四維空間中是可以的，他是如此的興奮，以至于把四元數的公式刻在了愛爾蘭的一座橋上。

旁白：“WTF，我讓你講三維物體的旋轉，你給我扯到四維空間上去。”

（不加說明，以下所說四元數全為單位四元數）
其實，四元數有四個變量，完全可以被看作一個四維向量。單位四元數（norm=1）則存在于四維空間的一個球面上。 $q_{a}q_{b}$ ，四元數 $q_{a}$ 乘以四元數 $q_{b}$ 其實看作（1）對 $q_{a}$ 進行 $q_{b}$ 左旋轉，或者（2）對 $q_{b}$ 進行 $q_{a}$ 右旋轉。所以從始至終，四元數定義的都是四維旋轉，而不是三維旋轉！任意的四維旋轉都可以唯一的拆分為一個左旋轉和一個右旋轉，表達出來就是 $q_{_{L}}pq_{_{R}}$ 。這里，我們對四元數（四維向量） $p$ 進行了一個 $q_{_{L}}$ 左旋轉和一個 $q_{_{R}}$ 右旋轉。結果當然是一個四元數，符合性質1。這個運算也同時符合性質2，3，4。

好了，說完了四維旋轉，我們終于可以說說三維旋轉了。說白了，三維旋轉就是四維旋轉的一個特例，就像二維旋轉是三維旋轉的一個特例一樣。說是特例其實不準確，準確的說是一個子集或者subgroup。為了進行三維旋轉運算，漢密爾頓首先在四維空間里劃出了一塊三維空間。漢密爾頓定義了一種純四元數（pure quaternion），其表達式為 $qw=(0,wx,wy,wz)$ 。純四元數第一項為零，它存在于四維空間的三維超平面上，與三維空間中的三維向量一一對應。然后，就有了我們常見的 $q*qw*q^{-1}$ 這種左乘單位四元數，右乘其共軛的表達式。我真心不知道漢密爾頓是怎么想出來的，不過回過頭來看，這個運算形式是為了限制其運算結果所在的空間。簡單的說，當對一個三維向量進行三維旋轉后，我們希望得到的是一個三維向量。（如果你真能得到一個四維向量，就不敢自己在家轉圈圈了吧，轉著轉著，就進入四次元了！）那么這個左乘單位四元數，右乘其共軛的運算保證了結果是一個在三維超平面上中的純四元數。

把左乘和右乘表達為矩陣形式會讓我們看的更清楚一些。依照 $qw$ 的定義， $q*qw*q^{-1}$ 的矩陣形式為
$\left[ \begin{array}{ c c c c} 1 & 0 & 0 & 0\\ 0 & q_{1}^2+q_{2}^2-q_{3}^2-q_{4}^2 & 2q_{2}q_{3}-2q_{1}q_{4} & 2q_{2}q_{4}+2q_{1}q_{3} \\ 0& 2q_{2}q_{3}+2q_{1}q_{4} & q_{1}^2-q_{2}^2+q_{3}^2-q_{4}^2 & 2q_{3}q_{4}-2q_{1}q_{2} \\ 0 & 2q_{2}q_{4}-2q_{1}q_{3} & 2q_{3}q_{4}+2q_{1}q_{2} & q_{1}^2-q_{2}^2-q_{3}^2+q_{4}^2 \end{array} \right] \left[ \begin{array}{ c } 0\\ wx\\ wy\\ wz \end{array} \right]$
很明顯，前面的矩陣雖然是一個4x4的四維旋轉矩陣，但是它只是在右下角3x3的區域內和一個單位矩陣有所不同。所以說，它是一個限制在三維超平面上的四維旋轉。如果表達式右邊不是共軛，而是任意四元數，那么我們所作的就是一個很普通的四維旋轉。如果只是左乘一個單位四元數，右邊什么都不乘，那么我們得到的是四維旋轉的一個子集，這個子集并不能保證結果限制在三維超平面上。如果只右乘，不左乘也是一樣一樣的。

說了這么多，對于堅持到最后的你，上圖一幅，以表感謝。

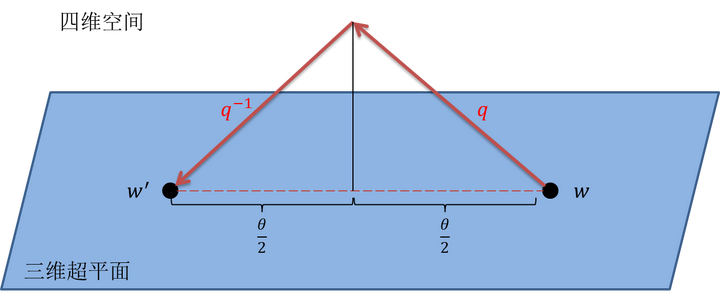
其實這張圖解釋了一個長久的疑問。為什么四元數 $q=(cos(\frac{\theta }{2} ),sin(\frac{\theta }{2} )*vx,sin(\frac{\theta }{2} )*vy,sin(\frac{\theta }{2} )*vz)$ 里用的是 $\frac{\theta }{2}$ 而不是 $\theta$ 。這是因為 $q$ 做的就是一個 $\frac{\theta }{2}$ 的旋轉，而 $q^{-1}$ 也做了一個 $\frac{\theta }{2}$ 的旋轉。我們進行了兩次旋轉，而不是一次，這兩次旋轉的結果是一個旋轉角為 $\theta$ 的旋轉。