堆和優先隊列
普通隊列:FIFO,LILO
優先隊列:出隊順序和入隊順序無關,和優先級相關。一個典型應用就是操作系統中。動態選擇優先級高的任務執行
堆的實現
最典型的堆就是二叉堆,就像是一顆二叉樹。這個堆的特點,下圖可以看出:
這里以最大堆為例,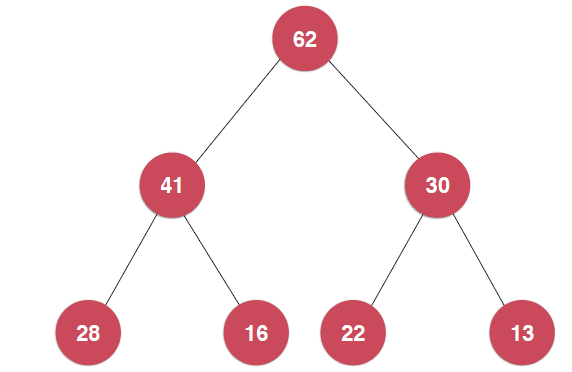 ,每一個節點都不大于其父親節點。另外,堆必須是一顆完全二叉樹,正因為此,我們可以使用數組來存儲二叉堆如下圖所示,給二叉堆自上而下,自左到右表上序號,
,每一個節點都不大于其父親節點。另外,堆必須是一顆完全二叉樹,正因為此,我們可以使用數組來存儲二叉堆如下圖所示,給二叉堆自上而下,自左到右表上序號,
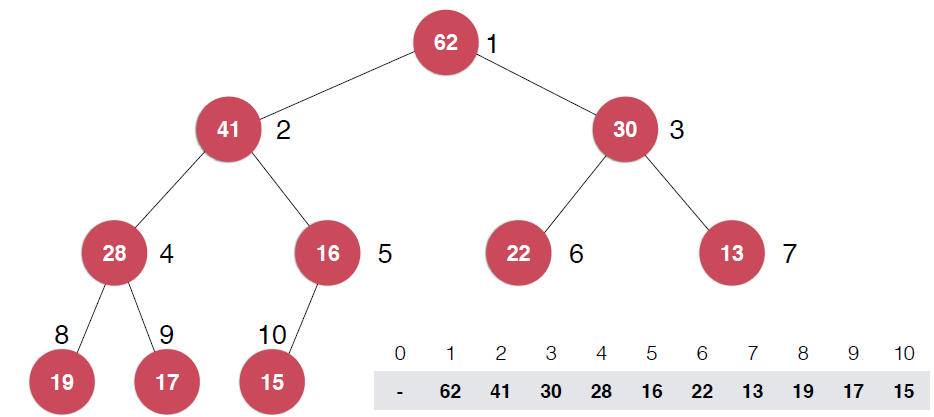
由圖中節點序號,可以看出,如果某個節點的序號為k,則其左子節點的序號是2*k,右子節點的序號是2*k+1,這里,與通常我們數組的規定不同,根節點是從1開始的,不是0,這也是堆的經典實現方式。不過從0開始標定,也會有類似性質,只是常數的變化。
下面就要實現最大堆,做成一個MaxHeap 類,最大堆中要存儲數據,為了通用性,將這個類做成一個模板類。這個最大堆首先得有一個存儲數據的數組,在用戶定義之前,我們不知道數組的大小,所以該數組是一個指針類型,相應的會在構造函數中初始化該數組。還需要一個int型的size來表示堆中元素數量。所以堆的基本框架如下:
1 template<typename Item>
2 class MaxHeap{
3 private:
4 Item* data;
5 int count;
6 private:
7 int shiftDown(int k){
8
9 }
10 public:
11 MaxHeap(int capacity){
12 data = new Item[capacity];
13 count=0;
14 }
15 ~MaxHeap(){
16 delete[] data;
17 }
18
19 int size(){return count;}
20
21 bool isEmpty(){return count==0;}
22 }; ?向堆中添加、刪除元素
添加元素
因為堆的性質,我們這里要用到一個添加元素時的核心操作。、;shiftUp,用下面的堆具體說一下思路
 ? ??
? ??
?
 ?
?
?
 ??
??
?
? ?
?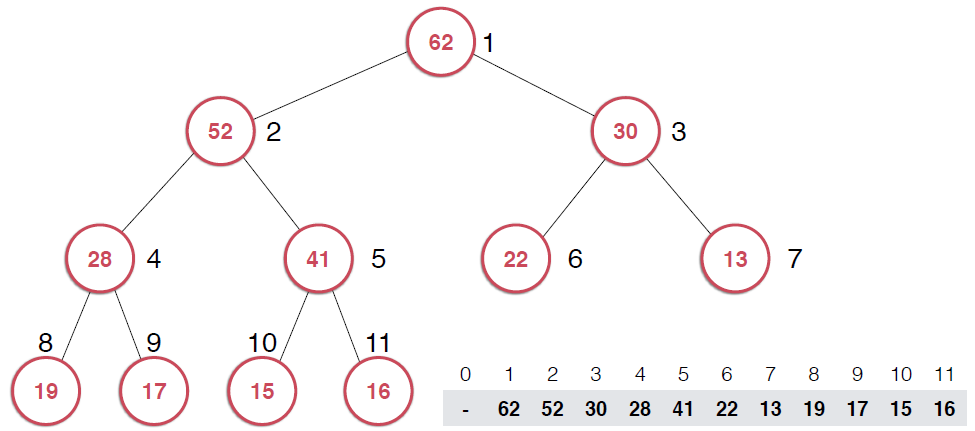
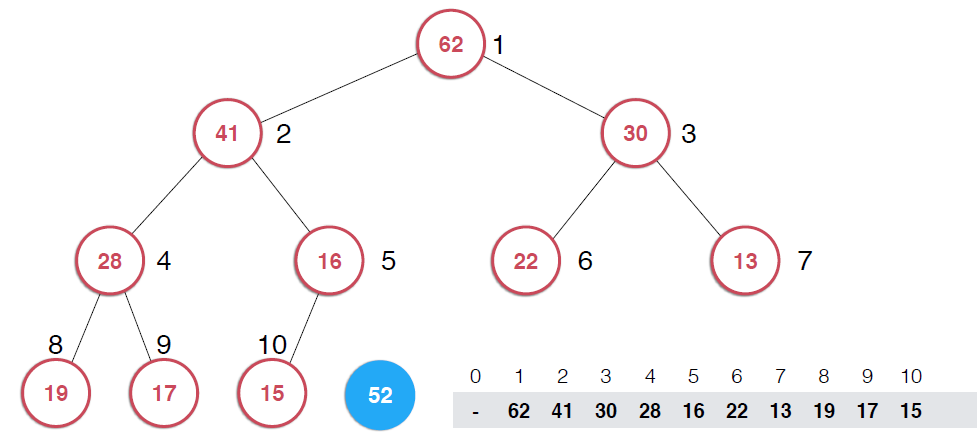
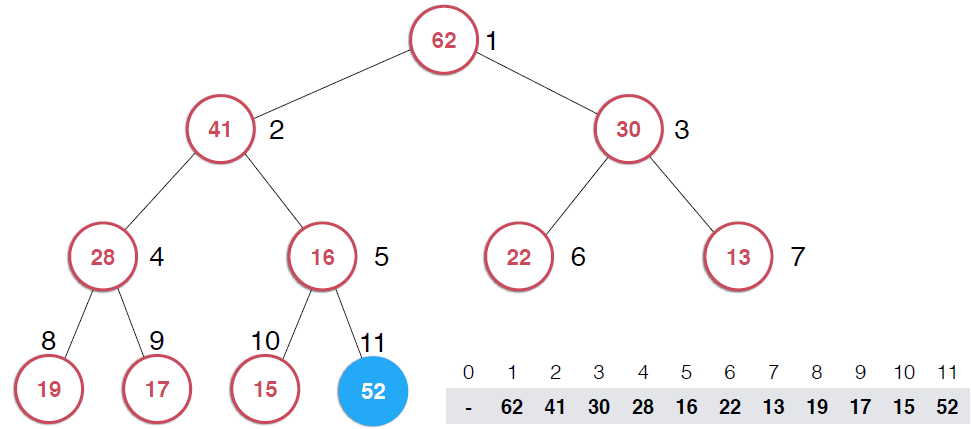
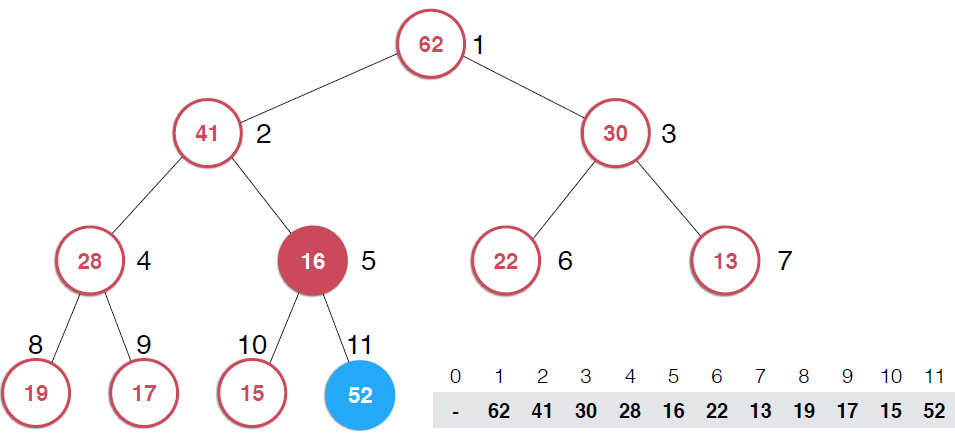
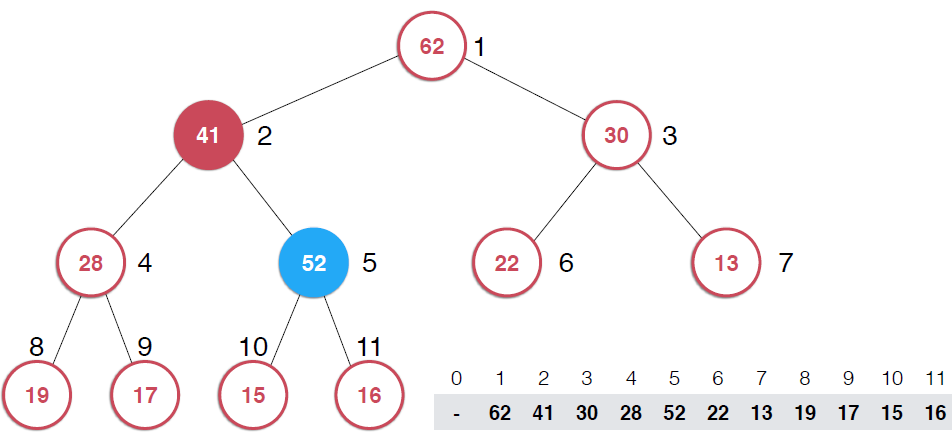
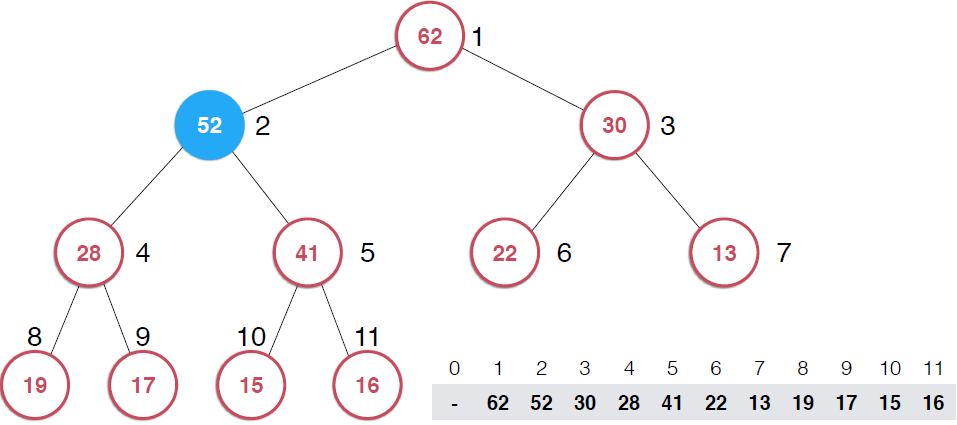
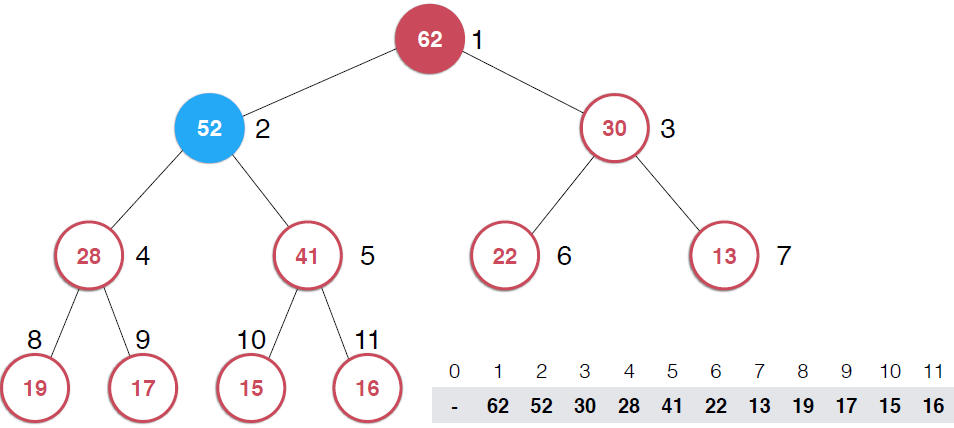
?因為是用數組存儲的堆中的元素,最初52加入的時候如第二幅圖所示,由于新元素的加入,這個堆已經不滿足最大堆的性質了,我們需要根據最大堆的性質調整,給52找到正確的位置,如何調整呢?:考查52的父節點,比52小,違背了最大堆的性質,所以交換之,這樣以52為根節點的子堆滿足了最大堆的性質,繼續考查新的堆中52的父節點,依然不滿足最大堆的定義,同樣的操作,繼續考查,直到整個堆滿足最大堆的性質。那么添加元素后只需要不斷調用shiftUp操作就可以了,具體代碼實現
1 // insert(Item) 2 2 void insert(Item item){ 3 3 data[count+1] =item; 4 4 count++; 5 5 shiftUp(count); 6 6 } 7 7 8 8 // shiftUp(int) 9 9 10 10 void shiftDown(int k){ 11 11 while(data[k/2]<data[k] && k>1){ 12 12 swap(data[k],data[k/2]); 13 13 k/=2; 14 14 } 15 15 }
但是,?data[count+1] =item;?有一個數組越界的潛在風險,所以,我們需要在類中再定義一個capacity的成員變量,并在構造函數中使用用戶指定的capacity初始化?this->capacity = capacity;?并且,在添加新元素之前assert一下,在insert(Item)函數中第三行之前加入?assert(count+1<=capacity);?當然,更好的方法就是一旦發現capacity不足夠,就分配新的空間,C++primer中在講容器的時候提到過,一般是采用倍增的方法,這里主要講堆,我自己也沒研究過,這里先Mark下,以后仔細想想具體實現,此處就先用這種簡單的方法防止數組越界。
從堆中取出元素
Note: 從堆中取出元素只能取出根節點的元素。
一旦取出對頂元素,就需要調整堆,使得堆這顆二叉樹依然滿足堆的性質。還是以圖的形式給出過程。
 ?
?
?
? ?
?
?
? ?
?
?
 ??
??
?
?
?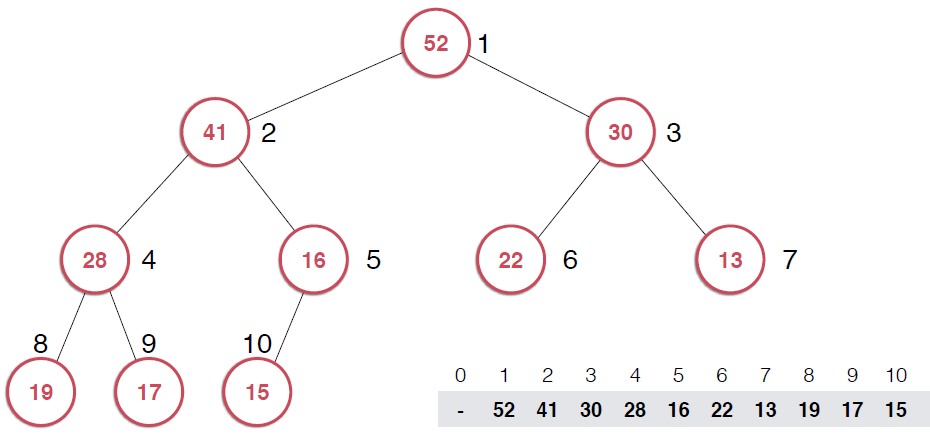
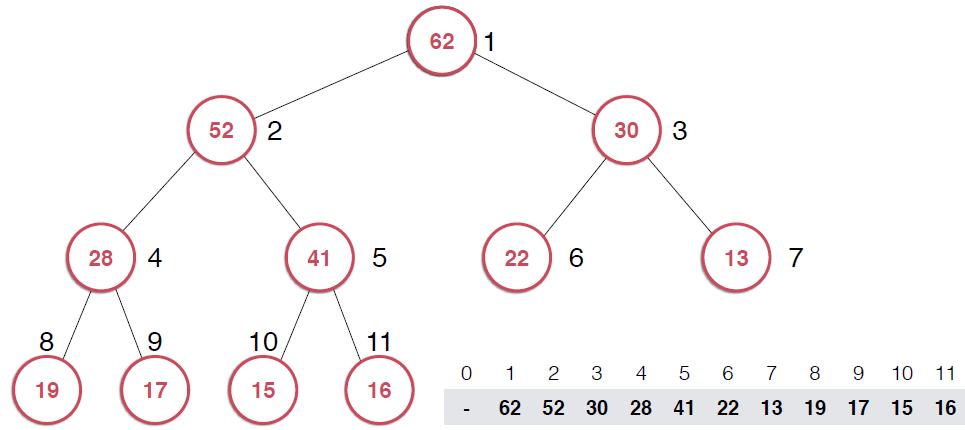
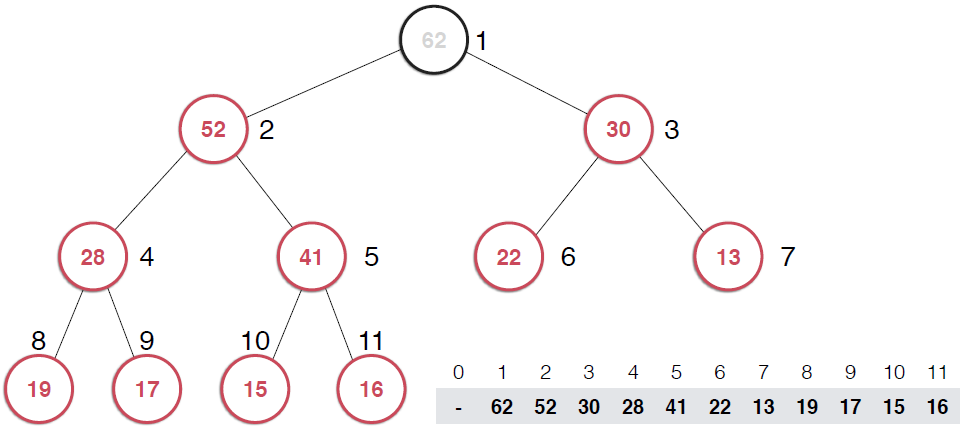
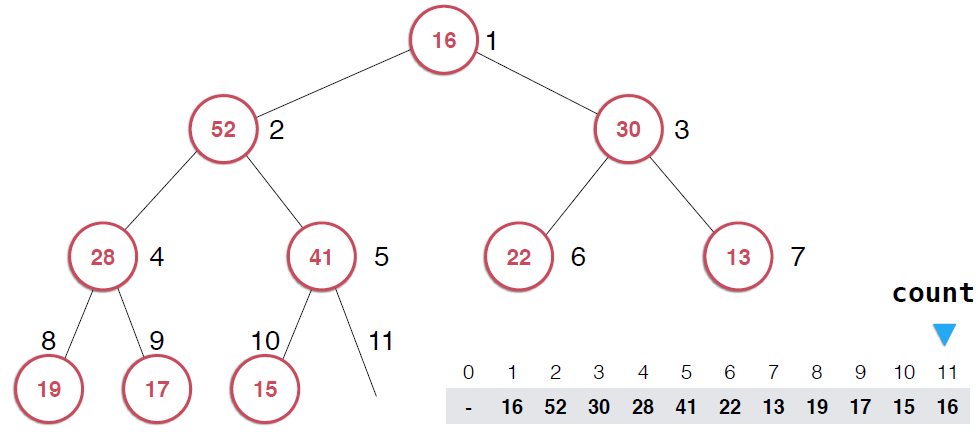
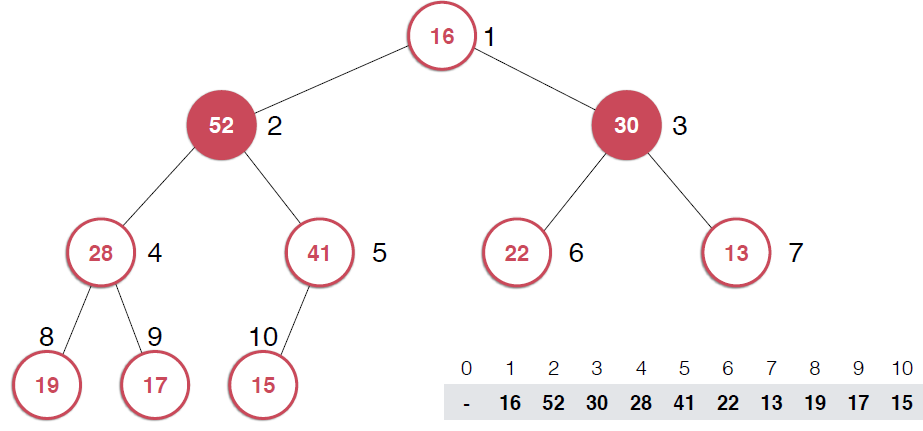
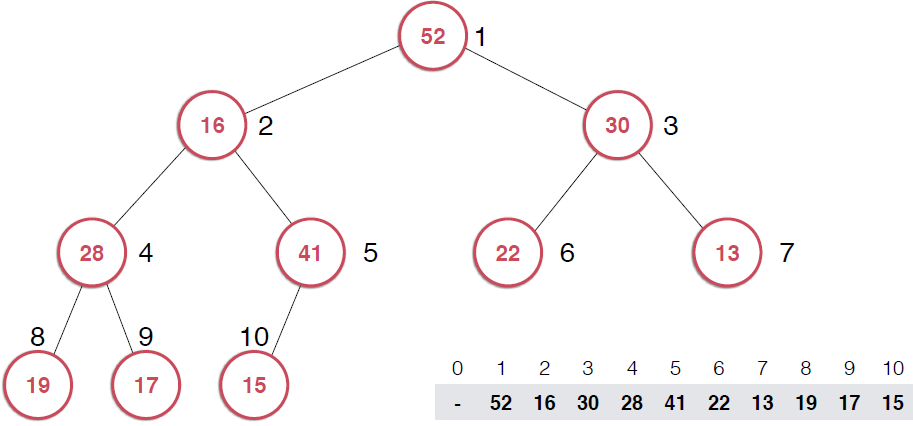
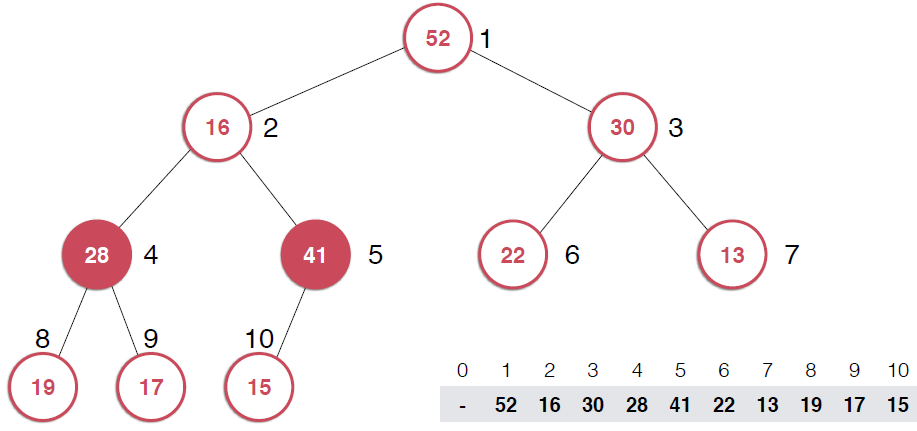
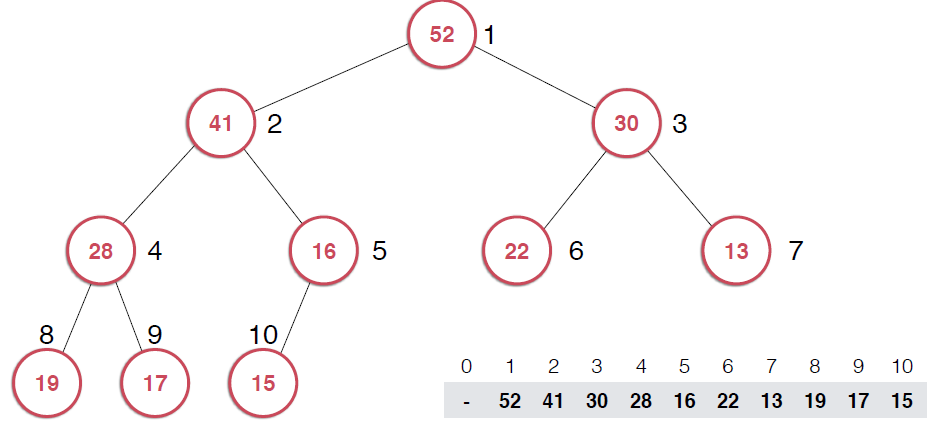
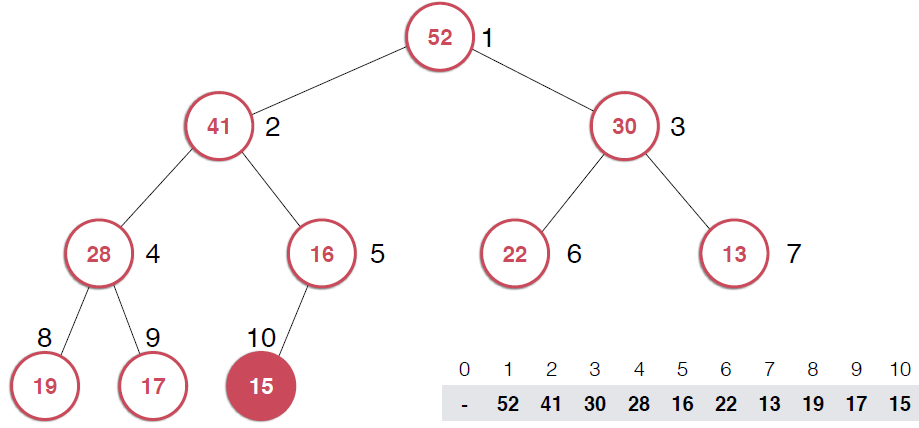
?由上面過程可以看出,一旦取出堆頂元素,就把堆中最后一個元素放到堆頂,不斷調整,直到這顆二叉樹再次滿足最大堆的性質。這個不斷調整的過程就是shiftDown 的過程。簡單說一下這個過程。現在16處在堆頂位置,比它的左右子節點都要小,最大堆的性質要求父親節點要大于子節點,所以,應該調整,向左還是向右是有左右的大小決定的,誰大跟誰換,這樣16跟52換,然后再考查新的堆,繼續考查16,直到16在它正確的位置。具體實現如下:
1 //shiftDown(int); 2 void shiftDown(int k){ 3 //int j = 2*k; 4 while(2*k<=count){ 5 int j = 2*k; 6 if(data[j]<data[j+1]) 7 j++; 8 if(data[k]<data[j]){ 9 swap(data[k],data[j]); 10 k = j; 11 } 12 } 13 } 14 15 //get the top of heap Item top() 16 Item get(){ 17 assert(count>0); 18 Item item = data[1]; 19 swap(data[1],data[count]) 20 count--; 21 //swap(data[]) 22 shiftDown(1); 23 return item; 24 }
前面給出了取出對頂元素的方法,如果,不斷取出堆頂元素并打印出來,就是一個從大到小的數組,由此,可以想到利用堆進行排序,這個排序接收一個數組和數組元素個數,創建一個heap類的對象,通過這個對象調用insert()函數和top() 函數即可實現,具體實現
1 void heap_sort(int arr[],int n){ 2 MaxHeap<int> maxHeap = MaxHeap(n); 3 for(int i = 0;i<n;i++) 4 maxHeap.insert(arr[i]); 5 for(int i = 0;i<n;i++) 6 arr[i] = maxHeap.top(); 7 }
上面實現的是從大到小的排序,要想從小到大排序,反向打印就可以,只需將第5行改為?for(int i = n-1;i>=0;i--)?
堆的heapify
前面提到了最大堆排序,我將上面的堆排序實現方式與歸并排序和快速排序時間做了一個比較,前面的堆排序的方式花費的時間較長,回顧一下,前面的堆排序需要將數組元素一個一個的插入堆中,利用堆不斷的調整,從堆中取出元素的時候也需要不斷的調整,使得二叉樹依然保有最大堆的性質,這種方式的效率顯然不高,說道這里,我想起來了,不斷調整過程中需要不斷的shiftUp和shiftDown,這兩個操作都需要swap()操作,前面講插入排序的時候提到過,swap操作相對于移動/賦值操作是低效的,所以,這里也是可以改進的,不過下面要說的是改進數組構成堆的方式,給定一個數組,我們讓這個數組形成一個堆的形狀,這個過程叫--Heapify.還是以圖片形式演示過程,下圖只給出了一部分過程的圖示
 ?
?
?
 ?
?
?
?
? ?
?
?
?
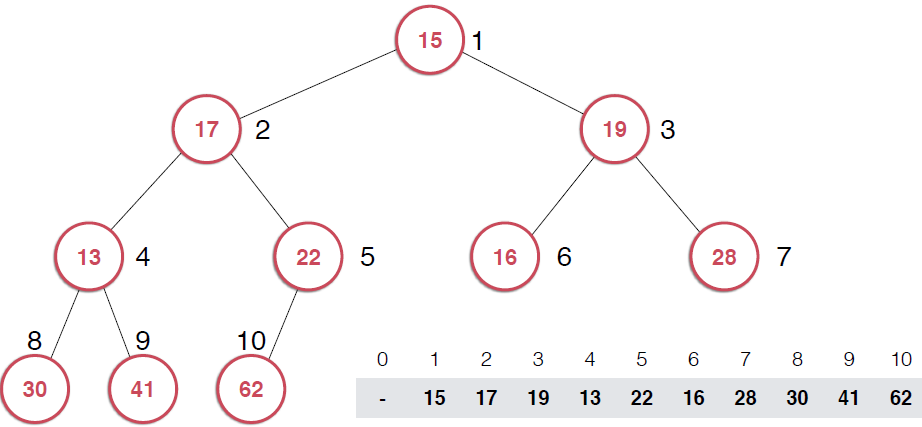
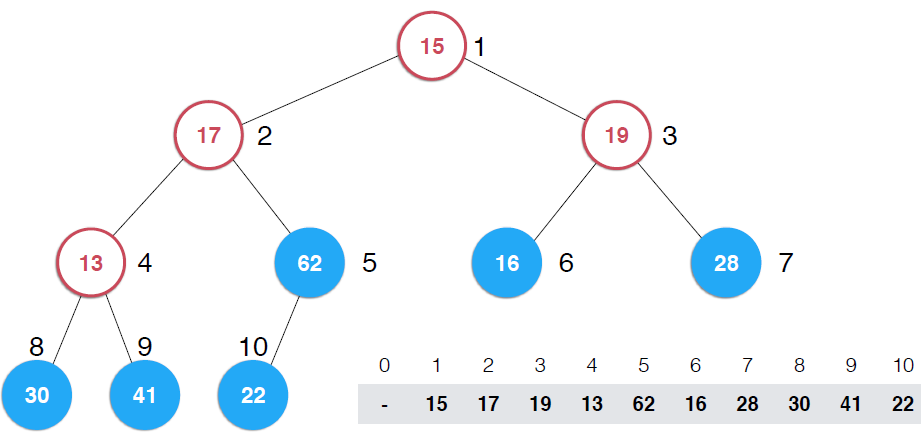
?看第一幅圖,右下角是一個數組,將該數組構建成一顆完全二叉樹,但是,這顆二叉樹不是堆,如果將這顆完全二叉樹根據對的性質調整成堆,那么,就將數組構造成了堆,調整過程就是上圖示過程
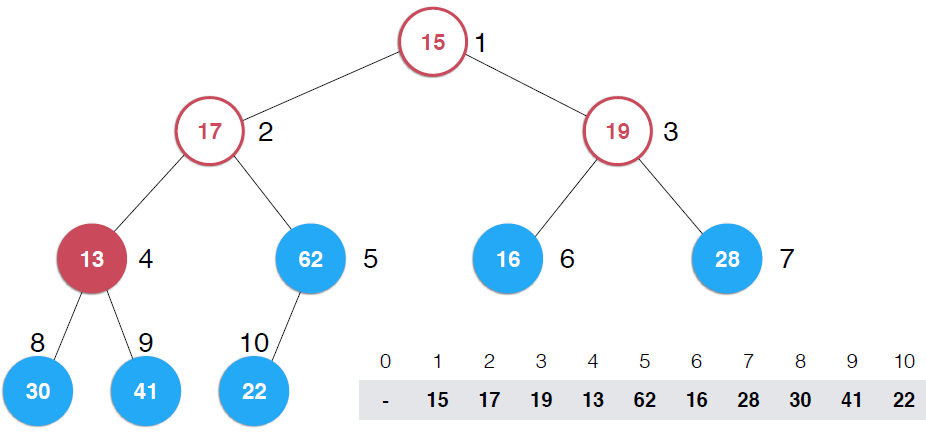
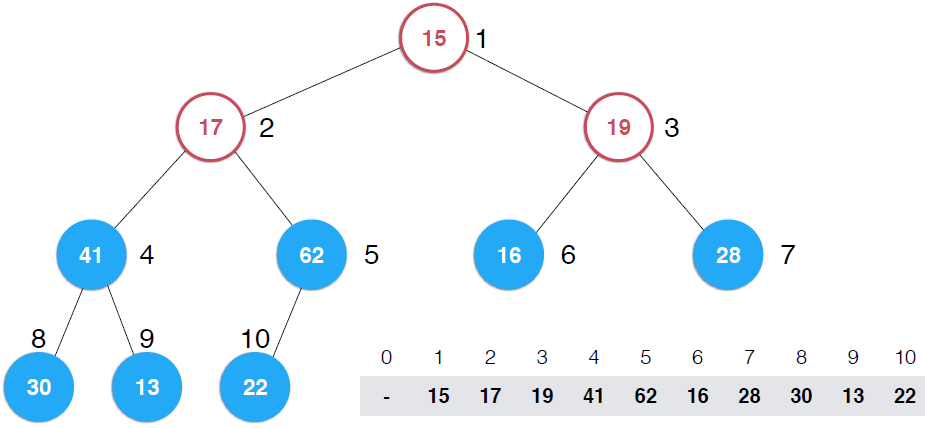
看第二幅圖中所有葉子節點,它們本身各自就是一個堆,還是以最大堆為例,一個最大堆,Note:一顆完全二叉樹,第一個非葉子節點是5,元素數目為10,可以多舉些例子,可以找出規律,一顆完全二叉樹第一個非葉子節點是k/2取整(k為完全二叉樹節點個數),這里是上取整,并且是從1開始而不是從0開始(可以證明的)。現在自下而上考查非葉子節點,第一個是5,它的值是32,以它為根的子樹不滿足最大堆的性質,它比子節點小,所以做一次shiftDown操作,接著考查4位置,13也比子節點小,再執行一次shiftDown操作,接著考查位置3,也不滿足,繼續執行shiftDown,再看2 ,17比它的子節點小,shiftDown,但是調整到5上,依然不滿足,繼續shiftDown,直到17在正確的位置上, 這時,以62為根的子樹滿足了最大堆性質,接著向上一層,樹頂元素不滿足,shiftDown,直到調整到15應該在的位置。可以構建一個構造函數接收一個數組和數組容量,代碼實現如下
1 MaxHeap(Item arr[],int n){ 2 data = new Item[n]; 3 capacity = n; 4 for(int i =0;i<n;i++) 5 data[i+1] = arr[i]; 6 count = n; 7 for(int k = n/2;k>0;k--) 8 shiftDown(k); 9 }
使用這個構造函數進行heapsort
1 void heap_sort2(int arr[],int n){ 2 MaxHeap<int> maxHeap = MaxHeap(arr,n); 3 for(int i = n-1;i>=0;i--) 4 arr[i] = maxHeap.top(); 5 }
再次測試,時間性能上比前面的堆排序快,但依然是比歸并排序和快速排序慢,不過堆排序通常用于動態數據的維護,而不是系統級別的排序。
將n個元素逐個插入到一個空堆中,時間復雜度是O(NlogN)的
但是heapify的過程,算法復雜度是O(N),這個,我沒有證明。只是看書上寫的
原地堆排序
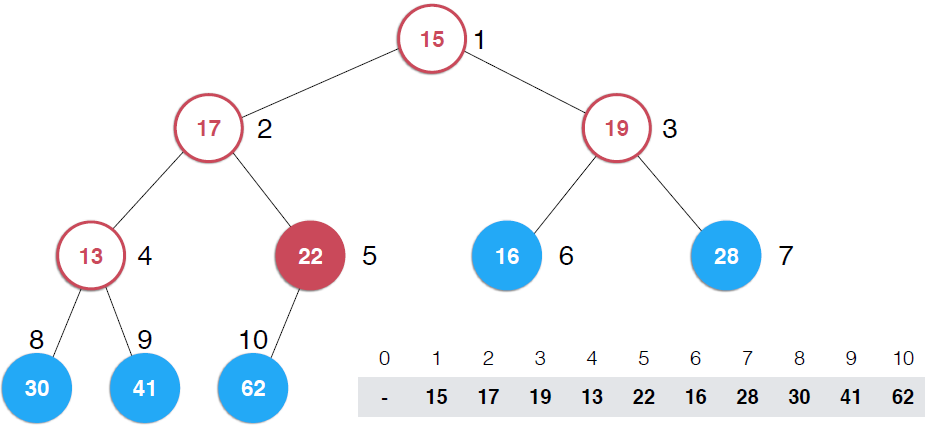
前面介紹的堆排序算法都需要將數據從數組放入堆中,再從堆中取出。這需要分配額外的空間,但是,根據堆排序的思想,整個數組的排序過程可以原地進行,不需要再分配額外空間。回想之前通過數組構造堆的過程可以看出一個數組其實可以把它看成一個堆,因此可以將數組通過heapify過程構建成堆,還是以最大堆為例。 ?這是一個數組形式排列的最大堆,堆頂元素v為整個數組中最大的,按照排序后的結果,v應該在數組尾部,所以將v與最后一個元素w交換,交換后這個數組不再是一個最大堆(橙色部分不再是最大堆),如何調整成最大堆,根據前面的,就是不斷的調用shiftDown,調整成一個最大堆(依然用暗紅色表示該部分是最大堆),藍色表示已經排序好的。
?這是一個數組形式排列的最大堆,堆頂元素v為整個數組中最大的,按照排序后的結果,v應該在數組尾部,所以將v與最后一個元素w交換,交換后這個數組不再是一個最大堆(橙色部分不再是最大堆),如何調整成最大堆,根據前面的,就是不斷的調用shiftDown,調整成一個最大堆(依然用暗紅色表示該部分是最大堆),藍色表示已經排序好的。
?
 ?
?
?
? ??
??
 ? 此時又重復上面的過程,繼續交換v和w,然后將未排序的部分調整成最大堆。
? 此時又重復上面的過程,繼續交換v和w,然后將未排序的部分調整成最大堆。
Note:由于整個過程在數組上原地進行,數組是從0開始索引的,所以在實現的時候注意調整,主要是shiftDown過程的索引,具體的就是父親節點與子節點索引的關系,舉個例子很容易看出來
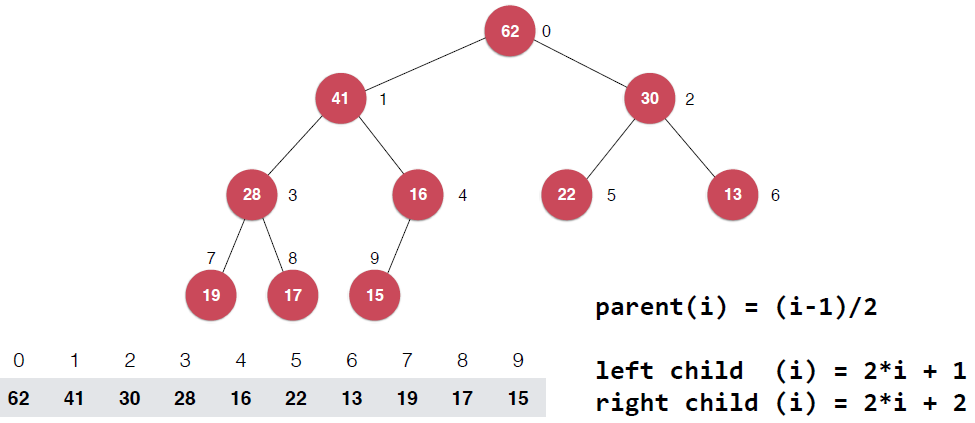
最后一個非葉子節點同時也變成了?(count-1)/2?,依然是上取整。
實現代碼如下:
?
1 void heapSort(int arr[],int n){ 2 //heapify 3 // index begins with 0 4 // the first leaf node which is not null (count-1)/2 5 for(int i = (n-1)/2;i>=0;i--) 6 __shiftDown(arr,n,i); 7 for(int i = n-1;i>=0;i--){ 8 swap(arr[i],arr[0]); 9 __shiftDown(arr,i,0); 10 } 11 } 12 13 void __shiftDown(int arr[],int n,int k){ 14 while(2*k+1<n){ 15 int j = 2*k+1; 16 if(arr[j]<arr[j+1] && j+1<n) 17 j+=1; 18 if(arr[k]<arr[j]){ 19 swap(arr[k],arr[j]); 20 k = j; 21 } 22 } 23 }
優化
之前提到過,用賦值操作代替交換操作會提升時間效率,在這里實現
1 void __shiftDown2(int arr[],int n,int k){ 2 int e = arr[k]; 3 while(2*k+1<n){ 4 int j = 2*k+1; 5 if(arr[j]<arr[j+1]) 6 j+=1; 7 if(e>=arr[j]) break; 8 arr[k] = arr[j]; 9 k = j; 10 } 11 arr[k] = e; 12 }
排序算法總結
到這里,所有排序算法都寫完了,下面的圖是我在GitHub上看到的關于排序算法的總結
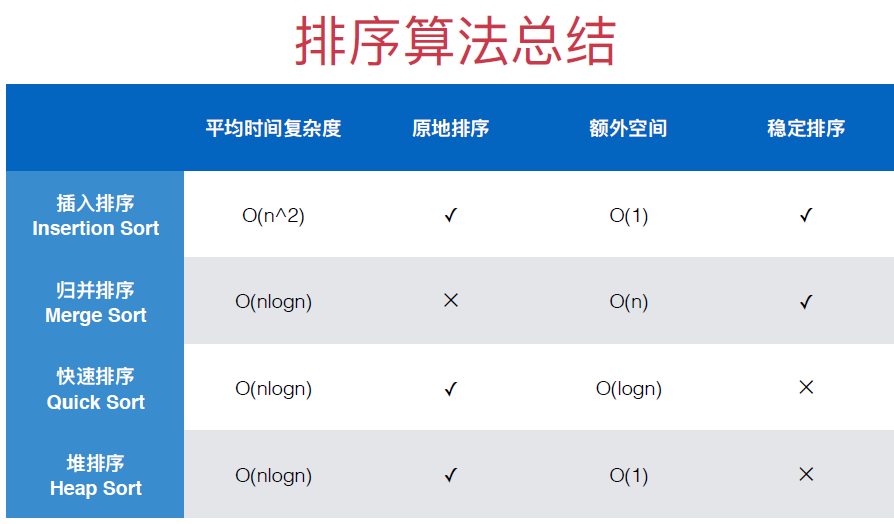
這里,有一個排序算法穩定性的概念,之前沒有提到過
算法穩定性:對于相等的元素在排序后,原來靠前的元素依然靠前,相等的元素的相對位置沒有發生改變
我覺得他給出的這個解釋的前半句非常好理解,對于算法穩定性。
?



![[Usaco2010 Nov]Visiting Cows](http://pic.xiahunao.cn/[Usaco2010 Nov]Visiting Cows)










)




