參考

3.11 模型選擇、欠擬合和過擬合

3.11.1 訓練誤差和泛化誤差

在解釋上述現象之前，我們需要區分訓練誤差（training error）和泛化誤差（generalization error）。通俗來講，前者指模型在訓練數據集上表現出的誤差，后者指模型在任意一個測試數據樣本上表現出的誤差的期望，并常常通過測試數據集上的誤差來近似。計算訓練誤差和泛化誤差可以使用之前介紹過的損失函數，例如線性回歸用到的平方損失函數和softmax回歸用到的交叉熵損失函數。

讓我們以高考為例來直觀地解釋訓練誤差和泛化誤差這兩個概念。訓練誤差可以認為是做往年高考試題（訓練題）時的錯誤率，泛化誤差則可以通過真正參加高考（測試題）時的答題錯誤率來近似。假設訓練題和測試題都隨機采樣于一個未知的依照相同考綱的巨大試題庫。如果讓一名未學習中學知識的小學生去答題，那么測試題和訓練題的答題錯誤率可能很相近。但如果換成一名反復練習訓練題的高三備考生答題，即使在訓練題上做到了錯誤率為0，也不代表真實的高考成績會如此。

在機器學習里，我們通常假設訓練數據集（訓練題）和測試數據集（測試題）里的每一個樣本都是從同一個概率分布中相互獨立地生成的。基于該獨立同分布假設，給定任意一個機器學習模型（含參數），它的訓練誤差的期望和泛化誤差都是一樣的。例如，如果我們將模型參數設成隨機值（小學生），那么訓練誤差和泛化誤差會非常相近。但我們從前面幾節中已經了解到，模型的參數是通過在訓練數據集上訓練模型而學習出的，參數的選擇依據了最小化訓練誤差（高三備考生）。所以，訓練誤差的期望小于或等于泛化誤差。也就是說，一般情況下，由訓練數據集學到的模型參數會使模型在訓練數據集上的表現優于或等于在測試數據集上的表現。由于無法從訓練誤差估計泛化誤差，一味地降低訓練誤差并不意味著泛化誤差一定會降低。

機器學習模型應關注降低泛化誤差。

3.11.2 模型選擇

在機器學習中，通常需要評估若干候選模型的表現并從中選擇模型。這一過程稱為模型選擇（model selection)。以多層感知機為例，我們可以選擇隱藏層的個數，以及每個隱藏層中隱藏單元個數和激活函數。為了得到有效的模型，我們通常要在模型選擇上下一番功夫。下面，我們來描述模型選擇中經常使用的驗證數據集（validation data set）。

3.11.2.1 驗證數據集

從嚴格意義上來講,測試集只能在所有超參數和模型選定后使用一次。不可以使用測試數據集選擇模型,如調參。由于無法從訓練誤差估計泛化誤差,因此也不應只依賴訓練數據選擇模型。鑒于此,我們可以預留一部分訓練數據集和測試數據集以外的數據來進行模型選擇。這部分數據稱為驗證數據集,簡稱驗證集(validation set)。

然而在實際應用中，由于數據不容易獲取，測試數據極少只使用一次就丟棄。因此，實踐中驗證數據集和測試數據集的界限可能比較模糊。從嚴格意義上講，除非明確說明，否則本書中實驗所使用的測試集應為驗證集，實驗報告的測試結果（如測試準確率）應為驗證結果（如驗證準確率）。

3.11.2.2 K折交叉驗證

由于驗證數據集不參與模型訓練,當訓練數據不夠時,預留大量的驗證數據顯得太奢侈。一種改善的方法是KK折交叉驗證（K-fold cross-validation）。在K折交叉驗證中,我們把原始訓練數據集分割成K個不重合的子數據集,然后我們做K次模型訓練和驗證。每一次,我們使用一個子數據集驗證模型,并使用其他K-1個子數據集來訓練模型。在這K次訓練和驗證中,每次用來驗證模型的子數據集都不同。最后,我們對這K次訓練誤差和驗證誤差分別求平均。

3.11.3 欠擬合和過擬合

欠擬合: 模型無法得到較低的誤差
過擬合: 模型在訓練集上的誤差遠遠小于在測試集上的誤差

3.11.3.1 模型復雜度

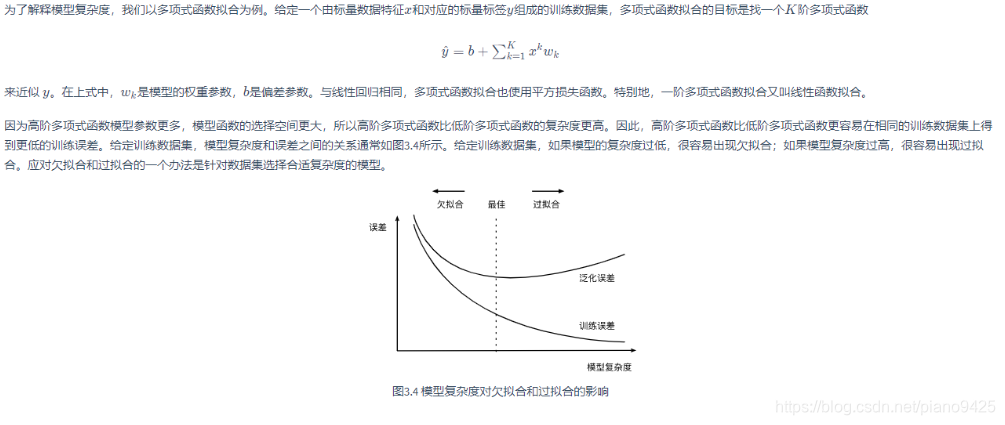
3.11.3.2 訓練數據集大小

影響欠擬合和過擬合的另一個重要因素是訓練數據集的大小。一般來說，如果訓練數據集中樣本數過少，特別是比模型參數數量（按元素計）更少時，過擬合更容易發生。此外，泛化誤差不會隨訓練數據集里樣本數量增加而增大。因此，在計算資源允許的范圍之內，我們通常希望訓練數據集大一些，特別是在模型復雜度較高時，例如層數較多的深度學習模型。

3.11.4 多項式函數擬合實驗

import torch
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l

3.11.4.1 生產數據集

n_train, n_nest, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
features = torch.randn((n_train + n_nest, 1))
poly_features = torch.cat((features, torch.pow(features, 2), torch.pow(features, 3)), 1)   # 按列拼起來
labels = (true_w[0] * poly_features[:,0] + true_w[1] * poly_features[:,1] + true_w[2] * poly_features[:, 2] + true_b)labels += torch.tensor(np.random.normal(0, 0.01, size = labels.size()), dtype=torch.float)

3.11.4.2 定義、訓練模型

def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None, legend=None, figsize=(3.5, 2.5)):d2l.set_figsize(figsize)d2l.plt.xlabel(x_label)d2l.plt.ylabel(y_label)d2l.plt.semilogy(x_vals, y_vals)if x2_vals and y2_vals:d2l.plt.semilogy(x2_vals, y2_vals, linestyle=":")d2l.plt.legend(legend)num_epochs, loss = 100, torch.nn.MSELoss()def fit_and_plot(train_features, test_features, train_labels, test_labels):net = torch.nn.Linear(train_features.shape[-1], 1)   # 線性,傳入輸入輸出即可batch_size = min(10, train_labels.shape[0])dataset = torch.utils.data.TensorDataset(train_features, train_labels)# Dataloader根據 TensorDataset、batch_size隨機取值返回train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle = True)# optim傳入模型的參數和學習率,返回一個優化器optimizer = torch.optim.SGD(net.parameters(), lr=0.01)train_ls, test_ls = [], []for _ in range(num_epochs):for X, y in train_iter:l = loss(net(X), y.view(-1, 1))optimizer.zero_grad()  # 將上一次的梯度清0l.backward()optimizer.step()train_labels = train_labels.view(-1, 1)test_labels = test_labels.view(-1, 1)train_ls.append(loss(net(train_features), train_labels).item())test_ls.append(loss(net(test_features), test_labels).item())print('final epoch: train loss', train_ls[-1], 'test loss', test_ls[-1])semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',range(1, num_epochs + 1), test_ls, ['train', 'test'])print('weight:', net.weight.data,'\nbias:', net.bias.data)

3.11.4.3 三階多項式函數擬合(正常)

fit_and_plot(poly_features[:n_train, :], poly_features[n_train:, :], labels[:n_train], labels[n_train:])

3.11.4.4 線性函數擬合(欠擬合)

fit_and_plot(features[:n_train, :], features[n_train:, :], labels[:n_train],labels[n_train:])

3.11.4.5 訓練樣本不足（過擬合）

fit_and_plot(poly_features[0:2, :], poly_features[n_train:, :], labels[0:2],labels[n_train:])