轉載自：https://blog.csdn.net/bone_ace/article/details/46239187

凸包問題的五種解法

2015年05月29日 17:58:51

閱讀數：33660

前言：

首先，什么是凸包？?
假設平面上有p0~p12共13個點，過某些點作一個多邊形，使這個多邊形能把所有點都“包”起來。當這個多邊形是凸多邊形的時候，我們就叫它“凸包”。如下圖：?
這里寫圖片描述

然后，什么是凸包問題？?
我們把這些點放在二維坐標系里面，那么每個點都能用 (x,y) 來表示。?
現給出點的數目13，和各個點的坐標。求構成凸包的點？

解一：窮舉法（蠻力法）

時間復雜度：O(n3）。?
思路：兩點確定一條直線，如果剩余的其它點都在這條直線的同一側，則這兩個點是凸包上的點，否則就不是。?
步驟：

將點集里面的所有點兩兩配對，組成 n(n-1)/2 條直線。
對于每條直線，再檢查剩余的 (n-2) 個點是否在直線的同一側。

如何判斷一個點 p3 是在直線 p1p2 的左邊還是右邊呢？（坐標：p1(x1,y1)，p2(x2,y2)，p3(x3,y3)）

這里寫圖片描述 ?
當上式結果為正時，p3在直線 p1p2 的左側；當結果為負時，p3在直線 p1p2 的右邊。

解二：分治法

時間復雜度：O(n㏒n)。?
思路：應用分治法思想，把一個大問題分成幾個結構相同的子問題，把子問題再分成幾個更小的子問題……。然后我們就能用遞歸的方法，分別求這些子問題的解。最后把每個子問題的解“組裝”成原來大問題的解。?
步驟：

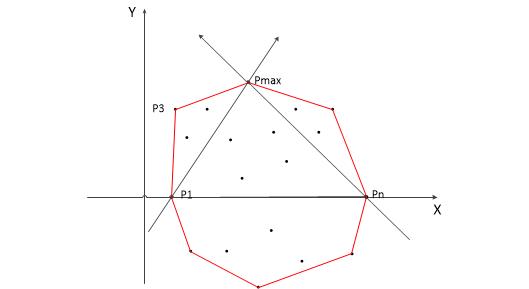
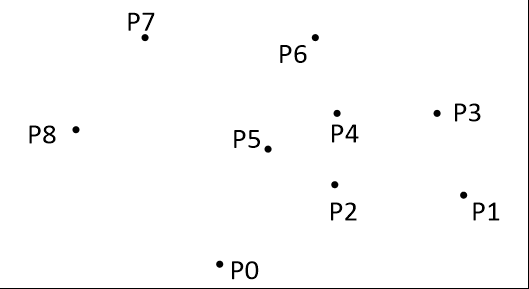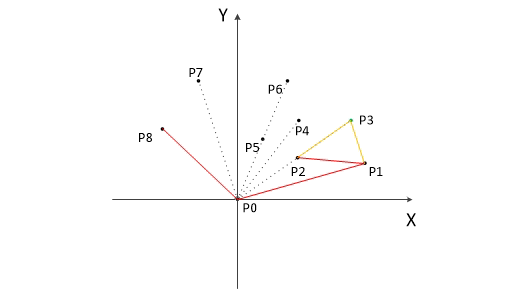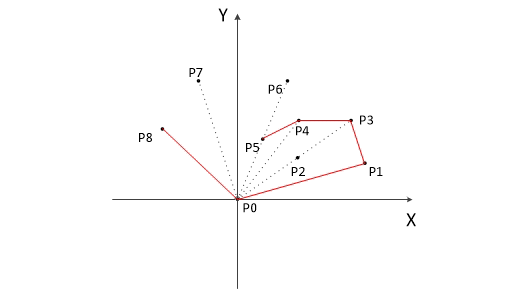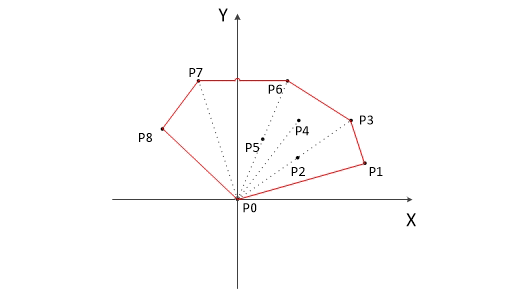
把所有的點都放在二維坐標系里面。那么橫坐標最小和最大的兩個點 P1 和 Pn 一定是凸包上的點（為什么呢？用反證法很容易證明，這里不詳講）。直線 P1Pn 把點集分成了兩部分，即 X 軸上面和下面兩部分，分別叫做上包和下包。
對上包：求距離直線 P1Pn 最遠的點，即下圖中的點 Pmax 。
作直線 P1Pmax 、PnPmax，把直線 P1Pmax 左側的點當成是上包，把直線 PnPmax 右側的點也當成是上包。
重復步驟 2、3。
對下包也作類似操作。

這里寫圖片描述

然而怎么求距離某直線最遠的點呢？我們還是用到解一中的公式：?
這里寫圖片描述 ?
設有一個點 P3 和直線 P1P2 。（坐標：p1(x1,y1)，p2(x2,y2)，p3(x3,y3)）?
對上式的結果取絕對值，絕對值越大，則距離直線越遠。

注意：在步驟一，如果橫坐標最小的點不止一個，那么這幾個點都是凸包上的點，此時上包和下包的劃分就有點不同了，需要注意。

解三：Jarvis步進法

時間復雜度：O(nH)。（其中 n 是點的總個數，H 是凸包上的點的個數）?
思路：

縱坐標最小的那個點一定是凸包上的點，例如圖上的 P0。
從 P0 開始，按逆時針的方向，逐個找凸包上的點，每前進一步找到一個點，所以叫作步進法。
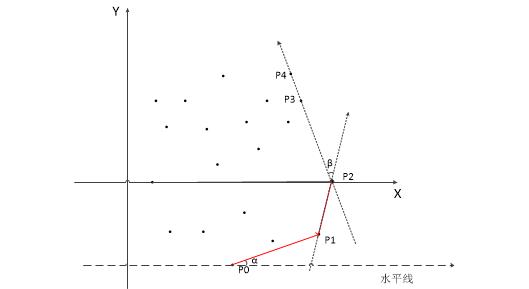
怎么找下一個點呢？利用夾角。假設現在已經找到 {P0，P1，P2} 了，要找下一個點：剩下的點分別和 P2 組成向量，設這個向量與向量P1P2的夾角為 β 。當 β 最小時就是所要求的下一個點了，此處為 P3 。

這里寫圖片描述

注意：

找第二個點 P1 時，因為已經找到的只有 P0 一個點，所以向量只能和水平線作夾角 α，當 α 最小時求得第二個點。
共線情況：如果直線 P2P3 上還有一個點 P4，即三個點共線，此時由向量P2P3 和向量P2P4 產生的兩個 β 是相同的。我們應該把 P3、P4 都當做凸包上的點，并且把距離 P2 最遠的那個點（即圖中的P4）作為最后搜索到的點，繼續找它的下一個連接點。

解四：Graham掃描法

時間復雜度：O(n㏒n)?
思路：Graham掃描的思想和Jarris步進法類似，也是先找到凸包上的一個點，然后從那個點開始按逆時針方向逐個找凸包上的點，但它不是利用夾角。?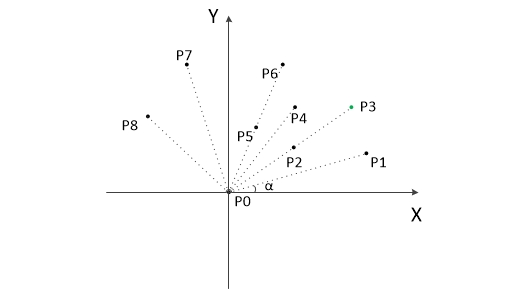
這里寫圖片描述 ?
步驟：

把所有點放在二維坐標系中，則縱坐標最小的點一定是凸包上的點，如圖中的P0。
把所有點的坐標平移一下，使 P0 作為原點，如上圖。
計算各個點相對于 P0 的幅角 α ，按從小到大的順序對各個點排序。當 α 相同時，距離 P0 比較近的排在前面。例如上圖得到的結果為 P1，P2，P3，P4，P5，P6，P7，P8。我們由幾何知識可以知道，結果中第一個點 P1 和最后一個點 P8 一定是凸包上的點。?
（以上是準備步驟，以下開始求凸包）?
以上，我們已經知道了凸包上的第一個點 P0 和第二個點 P1，我們把它們放在棧里面。現在從步驟3求得的那個結果里，把 P1 后面的那個點拿出來做當前點，即 P2 。接下來開始找第三個點：
連接P0和棧頂的那個點，得到直線 L 。看當前點是在直線 L 的右邊還是左邊。如果在直線的右邊就執行步驟5；如果在直線上，或者在直線的左邊就執行步驟6。
如果在右邊，則棧頂的那個元素不是凸包上的點，把棧頂元素出棧。執行步驟4。
當前點是凸包上的點，把它壓入棧，執行步驟7。
檢查當前的點 P2 是不是步驟3那個結果的最后一個元素。是最后一個元素的話就結束。如果不是的話就把 P2 后面那個點做當前點，返回步驟4。

最后，棧中的元素就是凸包上的點了。?
以下為用Graham掃描法動態求解的過程：?
這里寫圖片描述

代碼：poj1873

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<vector>
#define zero(a) (fabs((double)(a))<(1e-8))
using namespace std;
const int eps=1e-8;
struct tr{int x,y,v,l;
}s1[20],s[20];
int st[20];
int mul(tr p,tr u,tr v){//求叉積 return (p.x-u.x)*(v.y-u.y)-(v.x-u.x)*(p.y-u.y);
}
double dis(tr a,tr b){//求長度 return sqrt((double)(a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool cmp(tr a,tr b){//極角排序 if(mul(a,s[0],b)>0)//以最小點s[0]為基準排序 return true;else if(zero(mul(a,s[0],b))&&dis(s[0],a)<dis(s[0],b))return true;return false;
}
int mv,ct,nt;
double l2;
int do1(int n,int l1,int mv1,int c){int i,j;int x,y;double l;//要用的木材長度 if(n==1){l=0;}/*else if(n==2){l=dis(s[0],s[1])*2;}*/ else{ l=0;for(i=1;i<n;i++){if(s[0].y>s[i].y||(s[0].y==s[i].y&&s[0].x>s[i].x)){//將s[0]化為最小點，以便極角排序 swap(s[0],s[i]);}}sort(s+1,s+n,cmp);//排序 int top,cnt;st[0]=0;st[1]=1;tr a,b;top=2;cnt=2;while(cnt<n-1){//當 st[top]=cnt;//先放入當前點 top++;cnt++;a=s[st[top-1]];b=s[st[top-2]];while(mul(s[cnt],a,b)<eps){//以當前點的下一個點為標桿點來除去不合凸包條件的點（Graham掃描法）（如果標桿點在當前棧頂的兩個點組成的直線的右邊，則說明棧頂的點不是凸包上的點） top--;//去掉不合條件的點 a=b;//重新判斷當前棧頂的點 b=s[st[top-2]];}}st[top++]=n-1;//壓入最后一次的標桿點，它一定是凸包上的點，因為它在最左邊 for( i=0;i<top-1;i++){l+=dis(s[st[i]],s[st[i+1]]);}l+=dis(s[0],s[n-1]);//把這句代碼寫成了l+=dis(s[st[0]],s[st[n-1]]),卡了三個小時，QAQ，引以為戒啊 }//printf("%d %d\n",l1,l);if((l1-l)>=0){// 砍掉的樹可以把剩下的樹圍起來 if(mv1>mv){//剩下樹的價值要最大 l2=l1-l;nt=n;mv=mv1;ct=c;}else if(mv1==mv&&nt<=n){//價值相同時砍掉的樹要最少 l2=l1-l;nt=n;mv=mv1;ct=c;}}return 0;
}
int main(){int n,i,j,k=0;int a,b,cnt,c;int mv1;while(scanf("%d",&n)!=EOF&&n){k++;nt=0;for(i=0;i<n;i++){scanf("%d%d%d%d",&s1[i].x,&s1[i].y,&s1[i].v,&s1[i].l);}mv=0;ct=0;for(j=1;j<(1<<n)-1;j++){//二進制枚舉 //printf("%d\n",j);a=j,b=0;cnt=0;mv1=0;int l1=0;for(i=0;i<n;i++){if(((1<<i)&j)){//按位與 s[cnt++]=s1[i];//放入不砍的樹 mv1+=s1[i].v;//剩余的價值 }else{l1+=s1[i].l;//可以做籬笆的長度 }}if(mv>mv1)//剩下的價值小于最優的價值 continue;do1(cnt,l1,mv1,j);}printf("Forest %d\n",k);printf("Cut these trees:");for(i=0;i<n;i++)if(!((1<<i)&ct))  printf(" %d",i+1);printf("\n");printf("Extra wood: %.2f\n\n",l2);}return 0;
}