題目如標題，題目用到了分而治之的算法思想，以下是分而治之的定義：

“分而治之”（Divide andConquer）
是一種算法設計思想，它將一個大問題分解成相互獨立且相似的子問題，然后遞歸地解決這些子問題，最后將它們的解合并起來得到原問題的解。這種策略通常包括三個步驟：

分解（Divide）： 將原問題分解為若干個規模較小且相互獨立的子問題。

解決（Conquer）： 遞歸地解決這些子問題。如果子問題足夠小，可以直接求解。

合并（Combine）： 將子問題的解合并起來，形成原問題的解。

分而治之的思想常常應用在解決復雜問題的過程中，它可以提高算法的效率。一些著名的算法，如歸并排序、快速排序、二分查找等，都是采用了分而治之的策略。這種思想在許多計算機科學和算法領域都有廣泛的應用。此題目就是用了分而治之中的二分法，改善了題目的時間復雜度

這是自己大一暑假寫的逐次遍歷的方法

時間復雜度是O(n2)

#include<stdio.h>
#define MAX 100000
int main()
{int i,j,n,maxSum,tempSum,a[MAX];//定義數組大小的新方法，即通過宏定義 scanf("%d",&n);for(i=0;i<n;i++){scanf("%d",&a[i]);}maxSum=0;for(i=0;i<n;i++){tempSum=0;//保證每個初始值為0 for(j=i;j<n;j++)//循環不止有計數功能，有數組時，一定要注意下標 {tempSum+=a[j];if(tempSum>maxSum)//核心問題：可以算一步，判斷一步 maxSum=tempSum;}}printf("%d",maxSum);	}

以下是分而治之的方法

T ( N ) =O( N log N )
int MaxSum(int a[],int left,int right);
int threeOfMax(int a1,int a2,int a3);
int centerMaxSum(int a[],int left,int right);```c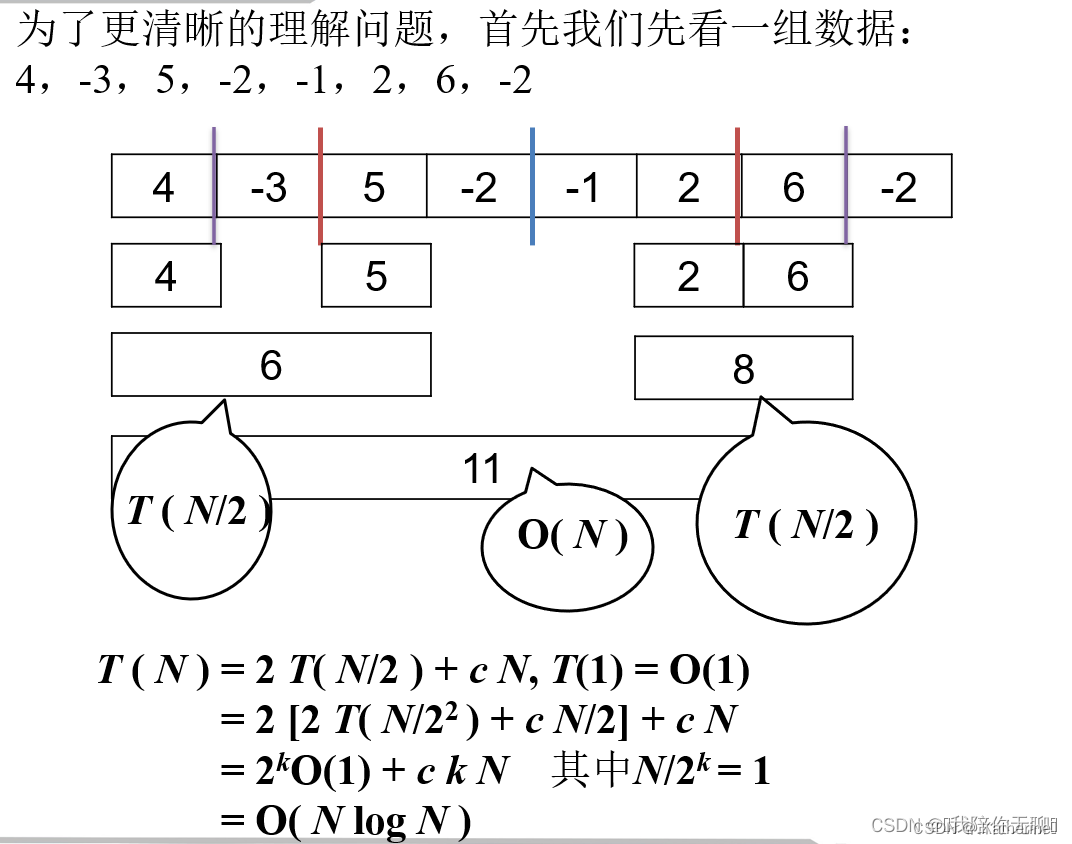

#include<stdio.h>
#define N 50
int MaxSum(int a[],int left,int right);
int centerMaxSum(int a[],int left,int right);
int threeOfMax(int a1,int a2,int a3);
int main(){int n;int a[N];printf("請設置數組位數n：\n");scanf("%d",&n);printf("請輸入數值：\n");for(int i = 0;i<n;i++){scanf("%d",&a[i]);}int left=0;int right=n-1; int maxSubSum = MaxSum(a,left,right);printf("最大子序列的和為:%d\n",maxSubSum);return 0;
} int MaxSum(int a[],int left,int right){int a1,a2,a3,i;int MaxLeftSum, MaxRightSum; //存放左右子問題的解int MaxLeftBorderSum, MaxRightBorderSum; //存放跨分界線的結果int LeftBorderSum, RightBorderSum;// 遞歸終止條件 直到分到最后一個元素 if(left==right){if( a[left] > 0 )return a[left];elsereturn 0;}int mid = (left+right)/2;// 劃分左邊a1 = MaxSum(a,left,mid);// 劃分右邊a2 = MaxSum(a,mid+1,right);// 求解s3 MaxLeftBorderSum = 0;LeftBorderSum = 0;for( i=mid; i>=left; i-- )   //從中線向左掃描{LeftBorderSum += a[i];if( LeftBorderSum > MaxLeftBorderSum )MaxLeftBorderSum = LeftBorderSum;} //左邊掃描結束MaxRightBorderSum = 0;RightBorderSum = 0;for( i=mid+1; i<=right; i++ )   //從中線向右掃描{RightBorderSum += a[i];if( RightBorderSum > MaxRightBorderSum )MaxRightBorderSum = RightBorderSum;} //右邊掃描結束 a3 =centerMaxSum(a,left,right);;//下面返回"治"的結果return threeOfMax( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );}
// 求解s3 
int centerMaxSum(int a[],int left,int right){int leftSum = 0;int rightSum = 0;int templeftSum = 0;int temprightSum = 0;int mid=(left+right)/2;for(int i = mid;i>=left;i--){templeftSum = templeftSum+a[i];if(templeftSum>leftSum)leftSum=templeftSum; }for(int j = mid+1;j<=right;j++){temprightSum = temprightSum+a[j];if(temprightSum>rightSum)rightSum=temprightSum;}return leftSum+rightSum;
}// 求解最大的子列和 
int threeOfMax(int a1,int a2,int a3){int maxSum = a1>a2?a1:a2;return maxSum>a3?maxSum:a3;
}

摘自