本系列側重于例題實戰與講解，希望能夠在例題中理解相應技巧。文章開頭相關基礎知識只是進行簡單回顧，讀者可以搭配課本或其他博客了解相應章節，然后進入本文正文例題實戰，效果更佳。

如果這篇文章對你有幫助，歡迎點贊與收藏~

基本概念

多元分析（Multivariate Analysis）是一種涉及多個變量的統計分析方法，是數理統計學中的一個重要分支。這種分析方法的內容豐富而復雜，具有獨特的視角和多樣的方法。在工程技術領域，多元分析由于其實用性和靈活性，深受工程技術人員的喜愛。它在許多工程領域都有廣泛的應用，比如在產品質量控制、風險評估、設計優化等方面都發揮著重要作用。

多元分析的核心在于同時考慮多個變量之間的相互關系。傳統的統計分析方法通常只考慮一個或兩個變量之間的關系，但在實際問題中，多個變量之間的交互作用往往對結果有著決定性的影響。因此，多元分析通過考察變量之間的這種復雜交互，能夠提供更加全面和深入的洞察。

此外，多元分析在處理大規模數據集時顯示出其獨特的優勢。隨著計算機技術的發展和數據采集能力的提高，工程師和研究人員現在能夠收集和分析以前無法想象的數據量。多元分析方法能夠有效處理這些大數據，揭示數據中隱藏的模式和趨勢，從而幫助決策者做出更加明智的決策。

聚類分析

聚類分析通常可以分為Q型和R型兩種。Q型聚類分析關注于樣本的分類，而R型聚類分析則側重于指標的分類。

Q型聚類分析

Q型聚類分析是一種將樣本根據它們之間的相似性進行分組的方法。這種方法特別適用于那些需要將個體或觀測值分為不同組或類別的情況。在這種分析中，相似性通常是通過計算樣本之間的距離來衡量的。距離越小，樣本間的相似性越高。

例如，在市場研究中，Q型聚類可以幫助識別具有相似購買行為或偏好的消費者群體。這種分析可以幫助企業更有效地針對特定群體進行營銷和產品開發。

R型聚類分析

R型聚類分析則是根據不同指標或變量之間的相似性來對它們進行分類。這種方法適用于尋找哪些變量或指標彼此之間聯系緊密，能夠共同表征某一現象或過程。

在經濟分析中，R型聚類可能用于識別哪些經濟指標通常同時變化，從而可以共同用于分析經濟趨勢或政策影響。同樣地，在環境科學中，R型聚類可以用來識別哪些環境因素共同影響生態系統的健康和穩定性。

主成分分析

主成分分析（PCA）是一種統計技術，用于簡化數據集。它通過減少數據集的維度，同時盡可能保留原始數據中的變異性來實現這一目的。PCA 在多個領域中都非常有用，特別是在處理具有多個變量或特征的復雜數據集時。

工作原理

1. 數據預處理：PCA 開始于將數據標準化，以便每個變量的貢獻權重相等。
2. 協方差矩陣計算：接著計算數據的協方差矩陣。協方差矩陣幫助識別數據中變量間的相關性。
3. 特征值和特征向量：然后計算協方差矩陣的特征值和特征向量。特征向量代表了數據的主成分方向，而特征值則表明了這些方向上的變異量。
4. 降維：最后，根據特征值的大小，選擇幾個最重要的特征向量，以降低數據集的維度。這些主成分捕捉了最多的數據變異性。

因子分析

因子分析（FA）是另一種數據降維技術，經常用于調查研究和心理測試。與 PCA 類似，因子分析旨在識別影響觀測變量的潛在變量（即因子）。

工作原理

1. 探索性因子分析（EFA）：EFA 的目的是探索數據，以識別潛在的因子結構。它不依賴于預先設定的模型。
2. 驗證性因子分析（CFA）：與 EFA 相反，CFA 是基于先前假設的因子結構來驗證數據的。
3. 因子提取：通過不同的數學方法（如主軸因子法或最大似然法），從觀測變量中提取因子。
4. 因子旋轉：為了使解釋更加清晰，通常會進行因子旋轉。這有助于使因子更容易被理解和解釋。

習題10.1

1. 題目要求

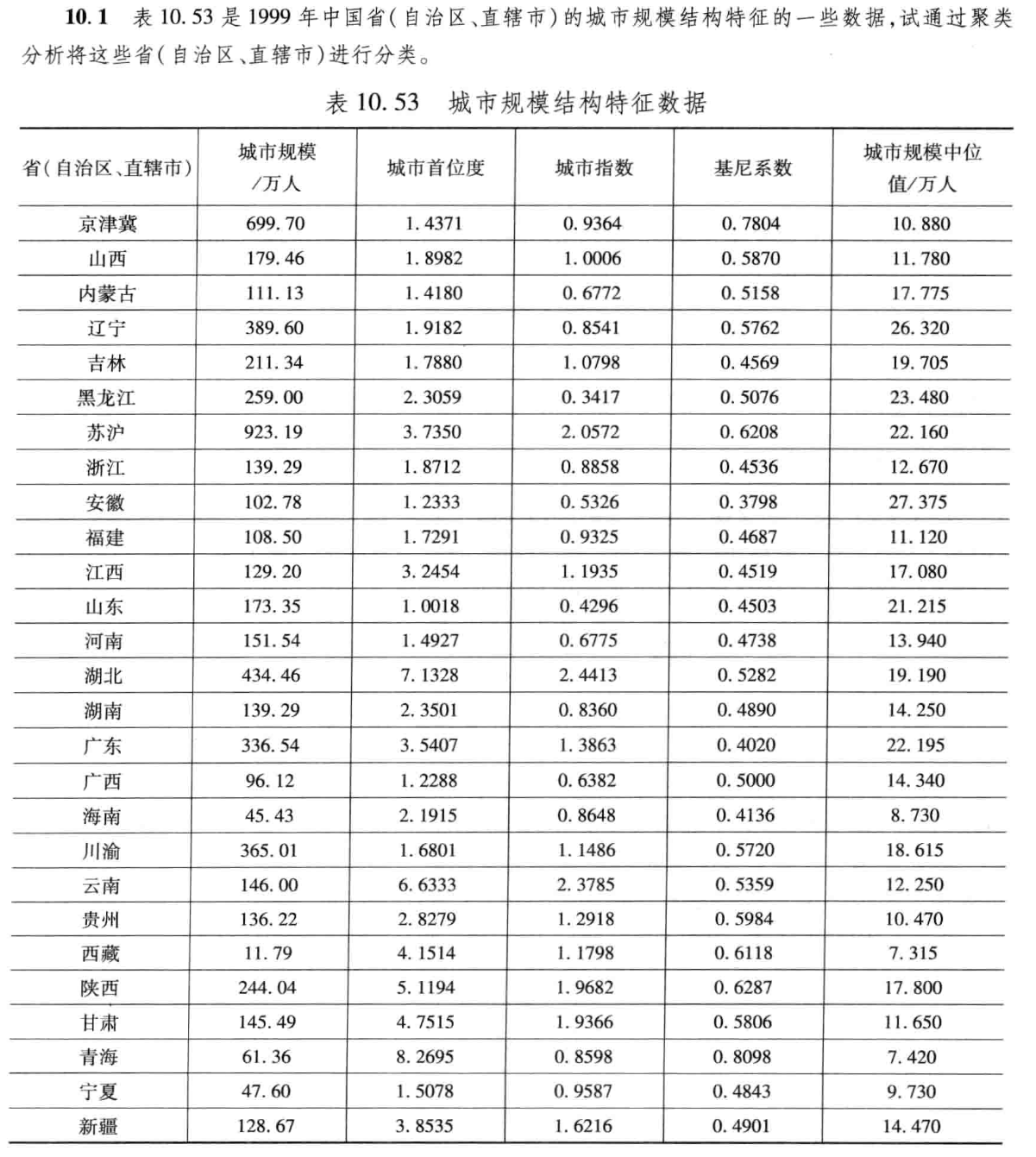
2.解題過程

解：

用 $i=1,\mathrm{2...},27$ 表示京津冀、山西、$...$、新疆27個省、自治區， $x_j(j=1,...,5)$ 分別表示指標變量城市規模城市首位度、城市指數、基尼系數、城市規模中位值。

（1）數據標準化

用 $a_{ij}$ 表示第i個省第j個指標變量的取值。

首先將各指標值 $a_{ij}$ 轉化為標準化指標值：
$$b_{ij}=\frac{a_{ij}?{\mu }_i}{s_j};i=1,2,?,27;j=1,?,5.$$
其中，${\mu }_j$ 是第j個指標的樣本均值，$s_j$ 是第j個指標的樣本標準差：
$${\mu }_j=\frac{1}{27}\sum _{i=1}^{27}{a}_{ij}$$

$$s_j=\sqrt{\frac{1}{26}\sum _{i=1}^{27}{\left(a_{ij}?{\mu }_j\right)}^2}(j=1,2,?,5)$$

（2）計算27個樣本點彼此之間的距離，構造距離矩陣：
$$d_{ik}=\sqrt{\sum _{j=1}^5{\left(b_{ij}?b_{kj}\right)}^2}$$
使用最短距離法來測量類與類之間的距離：
$$D(G_p,G_q)=\underset{i\in G_p,k\in G_q}{\min }\left|d_{ik}\right|$$
（3）

構造27個類，每一個類中只包含一個樣本點，每一類的平臺高度均為零。

（4）

合并距離最近的兩類為新類，并且以這兩類間的距離值作為聚類圖中的平臺高度。

（5）

若類的個數等于1，轉人步驟（6），否則，計算新類與當前各類的距離，回到步驟（4）。

（6）

繪制聚類圖，根據需要決定類的個數和類。

3.程序

求解的MATLAB程序如下：

clc, clear% 名稱
ss = {'京津冀', '山西', '內蒙古', '遼寧', '吉林', '黑龍江', '蘇滬', '浙江', ...'安徽', '福建', '江西', '山東', '河南', '湖北', '湖南', '廣東', ...'廣西', '海南', '川渝', '云南', '貴州', '西藏', '陜西', '甘肅', ...'青海', '寧夏', '新疆'};
% 數據
a = [699.70, 1.4371, 0.9364, 0.7804, 10.880; ...179.46, 1.8982, 1.0006, 0.5870, 11.780; ...111.13, 1.4180, 0.6772, 0.5158, 17.775; ...389.60, 1.9182, 0.8541, 0.5762, 26.320; ...211.34, 1.7880, 1.0798, 0.4569, 19.705; ...259.00, 2.3059, 0.3417, 0.5076, 23.480; ...923.19, 3.7350, 2.0572, 0.6208, 22.160; ...139.29, 1.8712, 0.8858, 0.4536, 12.670; ...102.78, 1.2333, 0.5326, 0.3798, 27.375; ...108.50, 1.7291, 0.9325, 0.4687, 11.120; ...129.20, 3.2454, 1.1935, 0.4519, 17.080; ...173.35, 1.0018, 0.4296, 0.4503, 21.215; ...151.54, 1.4927, 0.6775, 0.4738, 13.940; ...434.46, 7.1328, 2.4413, 0.5282, 19.190; ...139.29, 2.3501, 0.8360, 0.4890, 14.250; ...336.54, 3.5407, 1.3863, 0.4020, 22.195; ...96.12, 1.2288, 0.6382, 0.5000, 14.340; ...45.43, 2.1915, 0.8648, 0.4136, 8.730; ...365.01, 1.6801, 1.1486, 0.5720, 18.615; ...146.00, 6.6333, 2.3785, 0.5359, 12.250; ...136.22, 2.8279, 1.2918, 0.5984, 10.470; ...11.79, 4.1514, 1.1798, 0.6118, 7.315; ...244.04, 5.1194, 1.9682, 0.6287, 17.800; ...145.49, 4.7515, 1.9366, 0.5806, 11.650; ...61.36, 8.2695, 0.8598, 0.8098, 7.420; ...47.60, 1.5078, 0.9587, 0.4843, 9.730; ...128.67, 3.8535, 1.6216, 0.4901, 14.470];
% 使用zscore函數對矩陣a進行標準化處理
% zscore函數將每列的數據進行標準化，使其均值為0，標準差為1
% 標準化可以將不同變量之間的尺度差異消除，使得它們具有可比性
b = zscore(a)
% 使用pdist函數計算標準化后的矩陣b的成對距離
% pdist函數可以計算多維數據點之間的各種距離，默認情況下，pdist函數計算歐氏距離
d = pdist(b)
% 使用linkage函數進行層次聚類分析
% linkage函數將距離矩陣作為輸入，計算聚類之間的鏈接
% 它返回一個連接矩陣z，該矩陣描述了層次聚類的結構
z = linkage(d)
% 繪制樹狀圖
dendrogram(z, 'label', ss);

4.結果

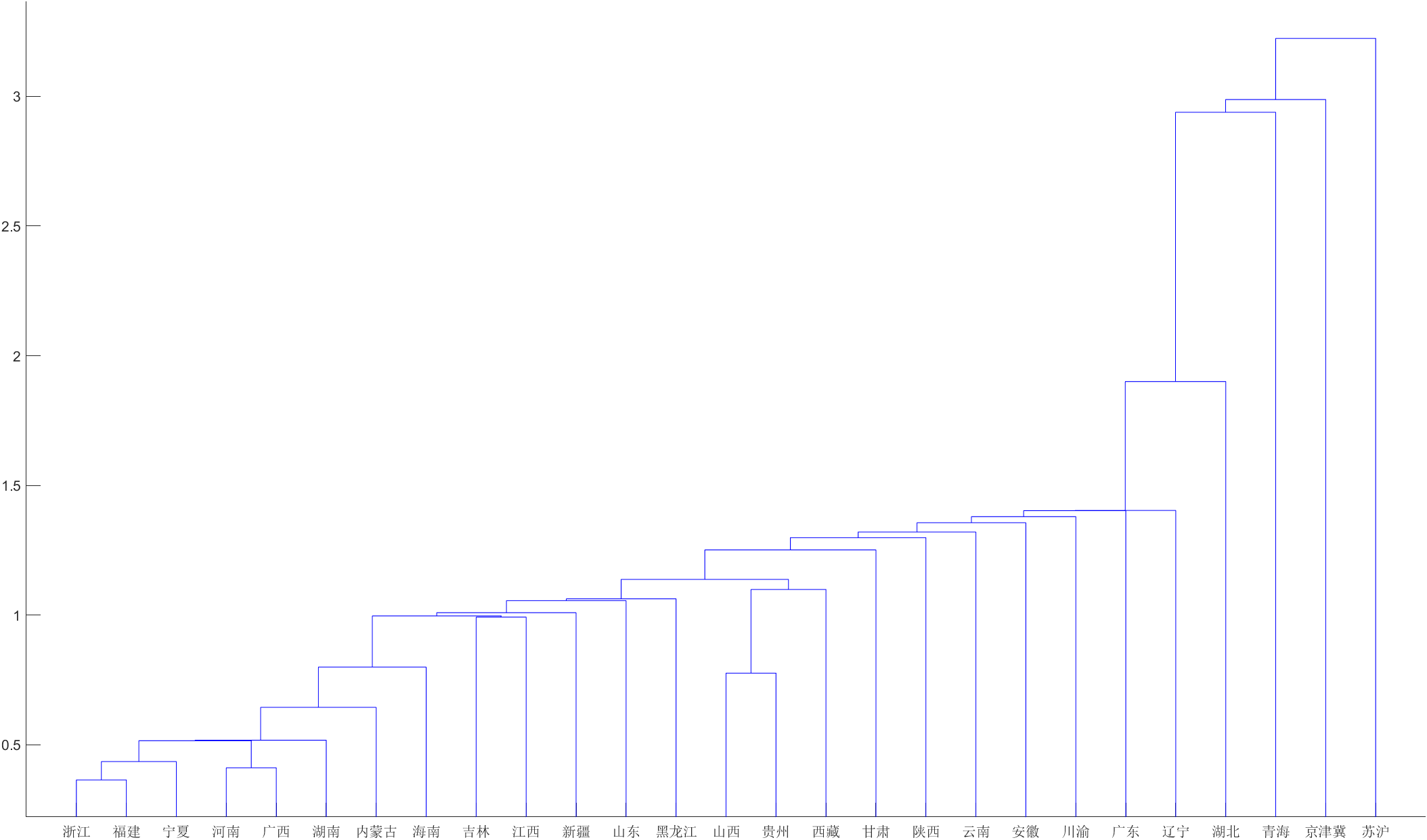
從聚類圖可以看出，蘇滬、京津冀、青海各自成一類，其余省和自治區成一類。

習題10.2

1. 題目要求

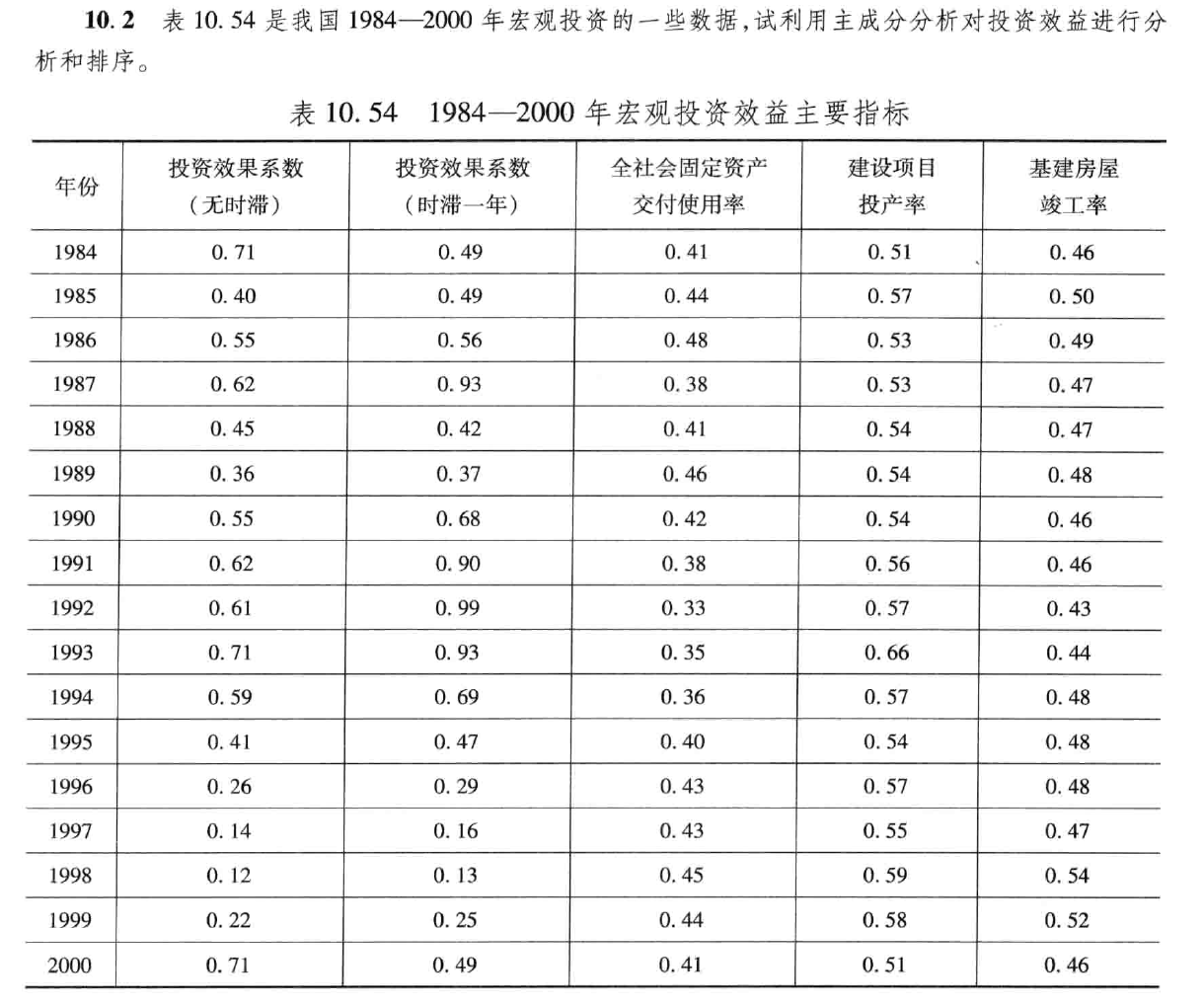
2.解題過程

解：

用 $x_1,x_2,...,x_5$ 分別表示投資效果系數（無時滯），投資效果系數（時滯一年），全社會固定資產交付使用率，建設項目投產率，基建房屋竣工率。

用 $i=1,2,...,17$ 分別表示1984年，1985年，… ，2000年，第i年第j個指標變量 $x_j$ 的取值記作 $a_{i}j$ ，構造矩陣 $A=(a_{ij}{)}_{17?5}$ 。

（1）數據標準化

首先將各指標值 $a_{ij}$ 轉化為標準化指標值：
$$b_{ij}=\frac{a_{ij}?{\mu }_i}{s_j};i=1,2,?,17;j=1,?,5.$$
其中，${\mu }_j$ 是第j個指標的樣本均值，$s_j$ 是第j個指標的樣本標準差：
$${\tilde{a}}_j=\frac{1}{17}\sum _{i=1}^{17}{a}_{ij}$$

$$s_j=\sqrt{\frac{1}{16}\sum _{i=1}^{17}{\left(a_{ij}?{\mu }_j\right)}^2}(j=1,2,?,5)$$

（2）計算相關系數矩陣R
$$R=(r_{ij}{)}_{5x5}$$

$$r_{ij}=\frac{{\sum }_{i=1}^{17}{\tilde{a}}_{ki}?{\tilde{a}}_{kj}}{17?1},i,j=1,2,?,5.$$

（3）計算特征值和特征向量

計算相關系數矩陣R的特征值，及對應的標準化特征向量 $u_1,u_2,...,u_5$ ，其中 $u_j=(u_{1j},u_{2j},?,u_{3j}{)}^{\mathsf{T}}$ ，由特征向量組成5個新的指標變量：
$$?\begin{array}{c}{y}_1=u_{11}{\tilde{x}}_1+u_{21}{\tilde{x}}_2+?+u_{51}{\tilde{x}}_5,\\ y_2=u_{12}{\tilde{x}}_1+u_{22}{\tilde{x}}_2+?+u_{52}{\tilde{x}}_5,\\ ?\\ y_5=u_{15}{\tilde{x}}_1+u_{25}{\tilde{x}}_2+?+u_{55}{\tilde{x}}_5.\end{array}$$
式中，y1是第一主成分，y2是第二主成分，…，y5是第五主成分。

（4）計算綜合評價值。

主成分yj的信息貢獻率：
$$b_j=\frac{{\lambda }_j}{{\sum }_{k=1}^5{\lambda }_k},j=1,2,?,5$$
主成分y1、y2、…、yp的累計貢獻率：
$${\alpha }_p=\frac{{\sum }_{k=1}^p{\lambda }_k}{{\sum }_{k=1}^5{\lambda }_k}$$
當ap接近于1 (ap = 0.85,0.90,0.95) 時，則選擇前p個指標變量作為p個主成分，代替原來5個指標變量，從而可對p個主成分進行綜合分析。

計算綜合評分：
$$Z=\sum _{j=1}^p{b}_j{y}_j.$$
其中bj是第j個主成分的信息貢獻率，根據綜合得分值就可以進行評價。

利用Matlab求得相關系數矩陣的前5個特征根及其貢獻率如下表：

序號	特征根	貢獻率	累計貢獻率
1	3.1343	62.6866	62.6866
2	1.1683	23.3670	86.0536
3	0.3502	7.0036	93.0572
4	0.2258	4.5162	97.5734
5	0.1213	2.4266	100.0000

可以看出，前三個特征根的累計貢獻率就達到93%以上，主成分分析效果很好。下面選取前三個主成分進行綜合評價。前三個特征根對應的特征向量如下表：

	x1	x2	x3	x4	x5
第1特征向量	0.490542	0.525351	-0.48706	0.067054	-0.49158
第2特征向量	-0.29344	0.048988	-0.2812	0.898117	0.160648
第3特征向量	0.510897	0.43366	0.371351	0.147658	0.625475

由此可得三個主成分分別為：
$$\begin{array}{l}{y}_1=0.491{\tilde{x}}_1+0.525{\tilde{x}}_2?0.487{\tilde{x}}_3+0.067{\tilde{x}}_5?0.492{\tilde{x}}_5,\\ y_2=?0.293{\tilde{x}}_1+0.049{\tilde{x}}_2?0.898{\tilde{x}}_4+0.161{\tilde{x}}_5,\\ y_3=0.511{\tilde{x}}_1+0.434{\tilde{x}}_1+0.43{\tilde{x}}_2+0.148{\tilde{x}}_4+0.625{\tilde{x}}_5,\end{array}$$
分別以三個主成分的貢獻率為權重,構建主成分綜合評價模型為：
$$Z=0.6269y_1+0.2337y_2+0.076y_3$$
把各年度的三個主成分值代入上式，可以得到各年度的綜合評價值以及排序結果如下表：

年代	1993	1992	1991	1994	1987	1990	1984	2000	1995
名次	1	2	3	4	5	6	7	8	9
綜合評價值	2.4464	l.9768	1.1123	0.8604	0.8456	0.2258	0.0531	0.0531	-0.2534

年代	1988	1985	1996	1986	1989	1997	1999	1998
名次	10	11	12	13	14	15	16	17
綜合評價值	0.2662	0.5292	0.7405	0.7789	0.9715	1.1476	-1.2015	-1.6848

3.程序

求解的MATLAB程序如下：

clc, clear
gj = [0.71, 0.49, 0.41, 0.51, 0.46; ...0.40, 0.49, 0.44, 0.57, 0.50; ...0.55, 0.56, 0.48, 0.53, 0.49; ...0.62, 0.93, 0.38, 0.53, 0.47; ...0.45, 0.42, 0.41, 0.54, 0.47; ...0.36, 0.37, 0.46, 0.54, 0.48; ...0.55, 0.68, 0.42, 0.54, 0.46; ...0.62, 0.90, 0.38, 0.56, 0.46; ...0.61, 0.99, 0.33, 0.57, 0.43; ...0.71, 0.93, 0.35, 0.66, 0.44; ...0.59, 0.69, 0.36, 0.57, 0.48; ...0.41, 0.47, 0.40, 0.54, 0.48; ...0.26, 0.29, 0.43, 0.57, 0.48; ...0.14, 0.16, 0.43, 0.55, 0.47; ...0.12, 0.13, 0.45, 0.59, 0.54; ...0.22, 0.25, 0.44, 0.58, 0.52; ...0.71, 0.49, 0.41, 0.51, 0.46];
gj = zscore(gj); % 將矩陣 gj 進行標準化處理，使得每一列的數據具有零均值和單位方差
r = corrcoef(gj); % 計算矩陣 gj 的相關系數矩陣 r，用于后續的主成分分析% 使用函數 pcacov 對相關系數矩陣 r 進行主成分分析
% 它返回三個輸出變量 x、y 和 z，分別表示主成分的系數矩陣、特征值和貢獻率
[x, y, z] = pcacov(r)
% 生成一個與 x 大小相同的矩陣 f，其中每個元素的值為主成分系數的符號
% 這樣做是為了確保主成分方向一致
f = repmat(sign(sum(x)), size(x, 1), 1);
x = x .* f % 將主成分系數矩陣 x 的每個元素與 f 對應位置的元素相乘，以確保主成分方向一致
num = 3; % 保留的主成分數量
df = gj * x(:, 1:num); % 計算投資數據矩陣 gj 與前 num 個主成分系數的乘積，得到降維后的數據矩陣 df
tf = df * z(1:num) / 100; % 計算降維后數據矩陣 df 與前 num 個特征值的乘積，并進行縮放，得到投資效益值的估計
[stf, ind] = sort(tf, 'descend'); % 對投資效益值進行降序排序，并返回排序后的結果 stf 和對應的索引 ind
stf = stf', ind = ind'

4.結果

各年度的綜合評價值以及排序結果如下表：

年代	1993	1992	1991	1994	1987	1990	1984	2000	1995
名次	1	2	3	4	5	6	7	8	9
綜合評價值	2.4464	l.9768	1.1123	0.8604	0.8456	0.2258	0.0531	0.0531	-0.2534

年代	1988	1985	1996	1986	1989	1997	1999	1998
名次	10	11	12	13	14	15	16	17
綜合評價值	0.2662	0.5292	0.7405	0.7789	0.9715	1.1476	-1.2015	-1.6848

如果這篇文章對你有幫助，歡迎點贊與收藏~