二分查找（Binary Search）算法，也叫折半查找算法，是一種針對有序數據集合的查找算法。

1-二分查找的思想

? ? ? ? 我們生活中猜數字的游戲，告訴你一個數據范圍，比如0-100，然后你說出一個數字，我告訴你的目標數字比你的大還是小，你繼續猜，根據二分查找的思想，你只要幾次就可以猜中。比如目標值68。

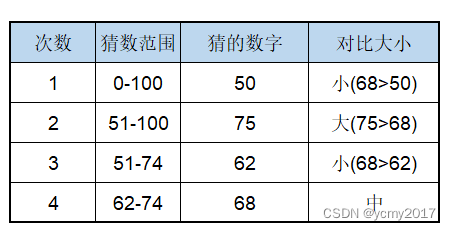
每次猜一個數字，通過告知結果后，排除掉一半的數字，這種思想就是二分查找。

? ? ? 二分查找針對的是一個有序的數據集合，查找思想有點類似分治思想。每次都通過跟區間的中間元素對比，將待查找的區間縮小為之前的一半，直到找到要查找的元素，或者區間被縮小為0。

? ? ? 折半的思想從而使得二分查找的時間復雜度是O(logn)。這是一種極其高效的時間復雜度；因為logn是一個非常“恐怖”的數量級，即便n非常非常大，對應的logn也很小。比如n等于2的32次方，大約是42億。也就是說，如果我們在42億個數據中用二分查找一個數據，最多需要比較32次。

2-二分查找實現

? ? ? ?假設數組中不存在重復的元素（數組中的元素有序，并且從小到大排序好），查找數組中是否存在某個元素，存在就返回元素在數組中的下標；不存在就返回-1。

   /*** 查詢數組中等于 target 的 索引* 數組中沒有重復的元素** @param array  待查找的數組* @param target 目標值* @return 數組下標索引，沒有查詢到返回-1*/
private static int binarySearch01(int[] array, int target) {int low = 0;int high = array.length - 1;while (low <= high) {int mid = low + ((high - low) >> 1);if (array[mid] == target) {return mid;}if (array[mid] > target) {high = mid - 1;}if (array[mid] < target) {low = mid + 1;}}return -1;}

3-二分查找的特點

(1)二分查找依賴的是順序表結構，簡單點說就是數組。
(2)二分查找針對的是有序數據。
(3)數據量太小不適合二分查找。但是如果數據之間的比較操作非常耗時，不管數據量大小，我都推薦使用二分查找。比如，數組中存儲的都是長度超過300的字符串，如此長的兩個字符串之間比對大小，就會非常耗時。我們需要盡可能地減少比較次數，而比較次數的減少會大大提高性能，這個時候二分查找就比順序遍歷更有優勢。
(4)數據量太大也不適合二分查找。二分查找的底層需要依賴數組這種數據結構，而數組為了支持隨機訪問的特性，要求內存空間連續，對內存的要求比較苛刻。

4-二分查找的變形問題

4.1-查找第一個值等于給定值的元素

? ? ? 上面的二分查找算法中，要求數組中存在不重復的數字，現在我們取消這個限制，查找數組中第一個值等于給定值的元素。

    /*** 查詢數組中第一個等于target的數字，返回數組的索引** @param array  目前數組* @param target 目標值* @return 數組下標索引，沒有查詢到返回-1*/private static int binarySearch02(int[] array, int target) {int low = 0;int high = array.length - 1;while (low <= high) {int mid = low + ((high - low) >> 1);if (array[mid] == target) {if ((mid == 0) || array[mid - 1] != target) {return mid;} else {high = mid - 1;}}if (array[mid] > target) {high = mid - 1;}if (array[mid] < target) {low = mid + 1;}}return -1;}

? ? ? 如果mid等于0，那這個元素已經是數組的第一個元素，那它肯定是我們要找的；如果mid不等于0，但a[mid]的前一個元素a[mid-1]不等于value，那也說明a[mid]就是我們要找的第一個值等于給定值的元素。

4.2-查找最后一個值等于給定值的元素

? ? ? 要求數組中存在不重復的數字，現在我們取消這個限制，查找數組中最后一個值等于給定值的元素。

    /*** 查詢數組中最后一個等于target的數字，返回數組的索引** @param array  目前數組* @param target 目標值* @return 數組下標索引，沒有查詢到返回-1*/private static int binarySearch03(int[] array, int target) {int low = 0;int maxIndex = array.length - 1;int high = array.length - 1;while (low <= high) {int mid = low + ((high - low) >> 1);if (array[mid] == target) {if ((mid == maxIndex) || array[mid + 1] != target) {return mid;} else {low = mid + 1;}}if (array[mid] > target) {high = mid - 1;}if (array[mid] < target) {low = mid + 1;}}return -1;}

? ? ? ?如果a[mid]這個元素已經是數組中的最后一個元素了，那它肯定是我們要找的；如果a[mid]的后一個元素a[mid+1]不等于value，那也說明a[mid]就是我們要找的最后一個值等于給定值的元素。如果我們經過檢查之后，發現a[mid]后面的一個元素a[mid+1]也等于value，那說明當前的這個a[mid]并不是最后一個值等于給定值的元素。我們就更新low=mid+1，因為要找的元素肯定出現在[mid+1, high]之間。

4.3-查找第一個大于等于給定值的元素

? ? ? ?對于a[mid]大于等于給定值value的情況，我們要先看下這個a[mid]是不是我們要找的第一個值大于等于給定值的元素。如果a[mid]前面已經沒有元素，或者前面一個元素小于要查找的值value，那a[mid]就是我們要找的元素。如果a[mid-1]也大于等于要查找的值value，那說明要查找的元素在[low, mid-1]之間，所以，我們將high更新為mid-1。

  /*** 查詢數組中查找第一個大于等于給定值的元素，返回數組的索引** @param array  目前數組* @param target 目標值* @return 數組下標索引，沒有查詢到返回-1*/private static int binarySearch04(int[] array, int target) {int low = 0;int high = array.length - 1;while (low <= high) {int mid = low + ((high - low) >> 1);if (array[mid] >= target) {if ((mid == 0) || array[mid - 1] < target) {return mid;} else {high = mid - 1;}} else {low = mid + 1;}}return -1;}

4.4-查找最后一個小于等于給定值的元素

? ? ? ?對于a[mid]小于等于給定值value的情況，我們要先看下這個a[mid]是不是我們要找的最后一個值小于等于給定值的元素。如果a[mid]后面已經沒有元素，或者后面一個元素大于要查找的值value，那a[mid]就是我們要找的元素。如果a[mid+1]也小于等于要查找的值value，那說明要查找的元素在[mid+1, high]之間，所以，我們將low更新為mid+1。

    /*** 查詢數組中查找最后一個小于等于給定值的元素，返回數組的索引** @param array  目前數組* @param target 目標值* @return 數組下標索引，沒有查詢到返回-1*/private static int binarySearch05(int[] array, int target) {int low = 0;int maxIndex = array.length - 1;int high = array.length - 1;while (low <= high) {int mid = low + ((high - low) >> 1);if (array[mid] <= target) {if ((mid == maxIndex) || array[mid + 1] > target) {return mid;} else {low = mid + 1;}}}return -1;}