介紹 networkx
networkx 支持創建簡單無向圖、有向圖和多重圖;內置許多標準的圖論算法,節點可為任意數據;支持任意的邊值維度,功能豐富,簡單易用
networkx 中的 Graph
Graph 的定義
Graph 是用點和線來刻畫離散事物集合中的每對事物間以某種方式相聯系的數學模型
網絡作為圖的一個重要領域,包含的概念與定義更多,如有向圖網絡、無向圖網絡等
Graph 在現實世界中隨處可見,如交通運輸圖、旅游圖、流程圖等。此處我們只考慮由點和線所組成的圖
Graph 的結構
一個 Graph 包含一個節點集合和一個邊集
在 networkx 中,一個節點可以是任意 hash 對象(除了 None 對象),一條邊也可以關聯任意的對象,像一個文本字符串,一幅圖像,一個 XML 對象,甚至是另一個圖或任意定制的節點對象
總結 :
Python中的None對象是不可以作為節點的類型的- 在
networkx中,節點與邊能夠存儲任意類型字典的屬性和任意其他豐富類型的數據
Graph 的分類
Graph:指無向圖(undirected Graph),即忽略了兩個節點間連邊的方向DiGraph:指有向圖(directed Graph),即考慮了兩個節點之間連邊的有向性MultiGraph:指多重無向圖,即兩個結點之間的邊數多于一條,又允許頂點通過同一條邊和自己關聯(即允許重邊和自環)MultiDiGraph:多重有向圖
g = nx.Graph() # 無向圖
dg = nx.DiGraph() # 有向圖
mg = nx.MultiGraph() # 多重無向圖
mdg = nx.MultiDiGraph() # 多重有向圖
g.clear() # 清空圖
networkx 語法
節點操作
添加節點
如果添加的節點和邊是已經存在的,是不會報錯的,
networkx會自動忽略掉已經存在的邊和節點的添加
import networkx as nx
import matplotlib.pyplot as pltG = nx.Graph() # 建立一個空的無向圖G
G.add_node('a') # 添加一個節點a
G.add_nodes_from(['b','c','d','e']) # 從一個列表中添加節點
H = nx.path_graph(10) # 返回由10個節點挨個連接的無向圖,有9條邊
G.add_nodes_from(H) # 創建一個子圖H加入G
G.add_node(H) # 直接將圖作為節點nx.draw(G, with_labels=True)
plt.show()print('圖中所有的節點', G.nodes())
print('圖中節點的個數', G.number_of_nodes())

刪除節點
# 刪除節點
G.remove_node(1) # 刪除指定節點
G.remove_nodes_from(['b','c','d','e']) # 刪除列表中的節點
nx.draw(G, with_labels=True)
plt.show()

邊操作
添加邊
# 添加邊
F = nx.Graph() # 創建無向圖
F.add_edge(11,12) # 指定節點之間添加一條邊
# 等價于
e=(13,14) # e 是一個元組
F.add_edge(*e) # python 中解包的過程F.add_edges_from([(1,2),(1,3)]) # 通過 list 來添加多條邊# 通過一個圖的邊來添加邊
H = nx.path_graph(10) # 返回由10個節點挨個連接的無向圖,有9條邊
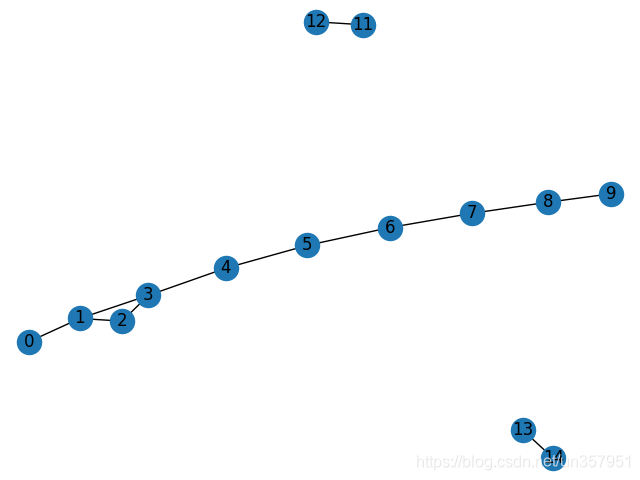
F.add_edges_from(H.edges()) # 不能寫作F.add_edges_from(H)nx.draw(F, with_labels=True)
plt.show()print('圖中所有的邊', F.edges())
print('圖中邊的個數', F.number_of_edges())
遍歷邊
# 快速遍歷每一條邊,可以使用鄰接迭代器實現,對于無向圖,每一條邊相當于兩條有向邊
G1 = nx.Graph()
G1.add_weighted_edges_from([(1,2,0.125), (1,3,0.75), (2,4,1.2), (3,4,0.275)])
for n, nbrs in G1.adjacency():for nbr, eattr in nbrs.items():data = eattr['weight']print('(%d, %d, %0.3f)' % (n,nbr,data))print('***********************************')# 篩選 weight 小于0.5的邊:
G2 = nx.Graph()
G2.add_weighted_edges_from([(1,2,0.125), (1,3,0.75), (2,4,1.2), (3,4,0.275)])
for n, nbrs in G2.adjacency():for nbr, eattr in nbrs.items():data = eattr['weight']if data < 0.5:print('(%d, %d, %0.3f)' % (n,nbr,data))
print('***********************************')# 一種方便的訪問所有邊的方法:
for u,v,d in G2.edges(data = 'weight'):print((u,v,d))
輸出:
(1, 2, 0.125)
(1, 3, 0.750)
(2, 1, 0.125)
(2, 4, 1.200)
(3, 1, 0.750)
(3, 4, 0.275)
(4, 2, 1.200)
(4, 3, 0.275)
***********************************
(1, 2, 0.125)
(2, 1, 0.125)
(3, 4, 0.275)
(4, 3, 0.275)
***********************************
(1, 2, 0.125)
(1, 3, 0.75)
(2, 4, 1.2)
(3, 4, 0.275)
刪除邊
# 刪除邊
F.remove_edge(1,2)
F.remove_edges_from([(11,12), (13,14)])nx.draw(F, with_labels=True)
plt.show()
屬性操作
屬性諸如 weight, labels, colors, 或者任何對象,你都可以附加到圖、節點或邊上。
對于每一個圖、節點和邊都可以在關聯的屬性字典中保存一個(多個)鍵-值對。
默認情況下這些是一個空的字典,但是我們可以增加或者是改變這些屬性
# 圖的屬性
G = nx.Graph(day='Monday') # 可以在創建圖時分配圖的屬性
print(G.graph)
G.graph['day'] = 'Friday' # 也可以修改已有的屬性
print(G.graph)
G.graph['name'] = 'time' # 可以隨時添加新的屬性到圖中
print(G.graph)
輸出:
{'day': 'Monday'}
{'day': 'Friday'}
{'day': 'Friday', 'name': 'time'}
# 節點的屬性
G = nx.Graph(day='Monday')
G.add_node(1, index='1th') # 在添加節點時分配節點屬性
print(G.nodes(data=True))
G.nodes[1]['index'] = '0th' # 通過G.nodes[][]來添加或修改屬性
print(G.nodes(data=True))
G.add_nodes_from([2,3], index='2/3th') # 從列表中添加節點時分配屬性
print(G.nodes(data=True))
輸出:
[(1, {'index': '1th'})]
[(1, {'index': '0th'})]
[(1, {'index': '0th'}), (2, {'index': '2/3th'}), (3, {'index': '2/3th'})]
# 邊的屬性
G = nx.Graph(day='manday')
G.add_edge(1,2,weight=10) # 在添加邊時分配屬性
print(G.edges(data=True))
G.add_edges_from([(1,3), (4,5)], len=22) # 從集合中添加邊時分配屬性
print(G.edges(data='len'))
G.add_edges_from([(3,4,{'hight':10}),(1,4,{'high':'unknow'})])
print(G.edges(data=True))
G[1][2]['weight'] = 100000 # 通過G[][][]來添加或修改屬性
print(G.edges(data=True))
輸出:
[(1, 2, {'weight': 10})]
[(1, 2, None), (1, 3, 22), (4, 5, 22)]
[(1, 2, {'weight': 10}), (1, 3, {'len': 22}), (1, 4, {'high': 'unknow'}), (3, 4, {'hight': 10}), (4, 5, {'len': 22})]
[(1, 2, {'weight': 100000}), (1, 3, {'len': 22}), (1, 4, {'high': 'unknow'}), (3, 4, {'hight': 10}), (4, 5, {'len': 22})]
圖轉化
# 有向圖轉化成無向圖
H = DG.to_undirected()
# 或者
H = nx.Graph(DG)# 無向圖轉化成有向圖
F = H.to_directed()
# 或者
F = nx.DiGraph(H)
其他操作
圖
degree(G[, nbunch, weight]):返回單個節點或nbunch節點的度數視圖。
degree_histogram(G):返回每個度值的頻率列表。
density(G):返回圖的密度。
info(G[, n]):打印圖G或節點n的簡短信息摘要。
create_empty_copy(G[, with_data]):返回圖G刪除所有的邊的拷貝。
is_directed(G):如果圖是有向的,返回true。
add_star(G_to_add_to, nodes_for_star, **attr):在圖形G_to_add_to上添加一個星形。
add_path(G_to_add_to, nodes_for_path, **attr):在圖G_to_add_to中添加一條路徑。
add_cycle(G_to_add_to, nodes_for_cycle, **attr):向圖形G_to_add_to添加一個循環。
節點
nodes(G):在圖節點上返回一個迭代器。
number_of_nodes(G):返回圖中節點的數量。
all_neighbors(graph, node):返回圖中節點的所有鄰居。
non_neighbors(graph, node):返回圖中沒有鄰居的節點。
common_neighbors(G, u, v):返回圖中兩個節點的公共鄰居。
邊
edges(G[, nbunch]):返回與nbunch中的節點相關的邊的視圖。
number_of_edges(G):返回圖中邊的數目。
non_edges(graph):返回圖中不存在的邊。










)
)
)






