文章目錄
- 1. 理論介紹
- 1.1. 從全連接層到卷積層
- 1.1.1. 背景
- 1.1.2. 從全連接層推導出卷積層
- 1.2. 卷積層
- 1.2.1. 圖像卷積
- 1.2.2. 填充和步幅
- 1.2.3. 多通道
- 1.3. 池化層(又稱匯聚層)
- 1.3.1. 背景
- 1.3.2. 池化運算
- 1.3.3. 填充和步幅
- 1.3.4. 多通道
- 1.4. 卷積神經網絡(LeNet)
- 1.4.1. 簡介
- 1.4.2. 組成
- 2. 實例解析
- 2.1. 實例描述
- 2.2. 代碼實現
- 2.2.1. 圖像中目標的邊緣檢測
- 2.2.1.1. 主要代碼
- 2.2.1.2. 完整代碼
- 2.2.1.3. 輸出結果
- 2.2.2. 在FashionMNIST數據集上訓練LeNet
- 2.2.2.1. 主要代碼
- 2.2.2.2. 完整代碼
- 2.2.2.3. 輸出結果
1. 理論介紹
1.1. 從全連接層到卷積層
1.1.1. 背景
- 使用多層感知機學習圖像數據面臨參數量巨大、數據量要求高的問題,因此這種缺少結構的網絡可能會變得不實用。
- 利用相近像素之間的相互關聯性,可以從圖像數據中學習得到有效的模型。
- 設計適合于計算機視覺的神經網絡架構的原則
- 平移不變性:不管檢測對象出現在圖像中的哪個位置,神經網絡的前面幾層應該對相同的圖像區域具有相似的反應。
- 局部性:神經網絡的前面幾層應該只探索輸入圖像中的局部區域,而不過度在意圖像中相隔較遠區域的關系。
1.1.2. 從全連接層推導出卷積層
- 假設多層感知機的輸入是二維圖像 X \mathbf{X} X,隱藏表示為二維張量 H \mathbf{H} H,且 X \mathbf{X} X和 H \mathbf{H} H具有相同的形狀, [ X ] i , j [\mathbf{X}]_{i,j} [X]i,j?和 [ H ] i , j [\mathbf{H}]_{i,j} [H]i,j?分別表示輸入圖像和隱藏表示中位置 ( i , j ) (i,j) (i,j)處的像素。為了使每個隱藏神經元都能接收到每個輸入像素的信息,我們將參數從權重矩陣替換為四維權重張量 W \mathbf{W} W,偏置為 U \mathbf{U} U,則全連接層可表示為
[ H ] i , j = [ U ] i , j + ∑ k ∑ l [ W ] i , j , k , l [ X ] k , l = [ U ] i , j + ∑ a ∑ b [ V ] i , j , a , b [ X ] i + a , j + b \begin{aligned} [\mathbf{H}]_{i,j} &=[\mathbf{U}]_{i,j}+\sum_k\sum_l{[\mathbf{W}]_{i,j,k,l}}{[\mathbf{X}]_{k,l}} \\ &=[\mathbf{U}]_{i,j}+\sum_a\sum_b{[\mathbf{V}]_{i,j,a,b}}{[\mathbf{X}]_{i+a,j+b}} \end{aligned} [H]i,j??=[U]i,j?+k∑?l∑?[W]i,j,k,l?[X]k,l?=[U]i,j?+a∑?b∑?[V]i,j,a,b?[X]i+a,j+b??
其中, [ V ] i , j , a , b = [ W ] i , j , i + a , j + b [\mathbf{V}]_{i,j,a,b}=[\mathbf{W}]_{i,j,i+a,j+b} [V]i,j,a,b?=[W]i,j,i+a,j+b?,索引 a a a和 b b b通過在正偏移和負偏移之間移動覆蓋了整個圖像。 - 平移不變性意味著檢測對象在輸入 X \mathbf{X} X中的平移,應該僅導致隱藏表示 H \mathbf{H} H中的平移,即 U \mathbf{U} U和 V \mathbf{V} V不依賴與 ( i , j ) (i,j) (i,j)的值,則有
{ [ V ] i , j , a , b = [ V ] a , b [ U ] i , j = u \begin{cases} [\mathbf{V}]_{i,j,a,b} &= [\mathbf{V}]_{a,b}\\ [\mathbf{U}]_{i,j}&=u \end{cases} {[V]i,j,a,b?[U]i,j??=[V]a,b?=u?
因而我們可以簡化 H \mathbf{H} H的定義為
[ H ] i , j = u + ∑ a ∑ b [ V ] a , b [ X ] i + a , j + b [\mathbf{H}]_{i,j} = u + \sum_a\sum_b{[\mathbf{V}]_{a,b}}{[\mathbf{X}]_{i+a,j+b}} [H]i,j?=u+a∑?b∑?[V]a,b?[X]i+a,j+b? - 局部性意味著當 ∣ a ∣ > Δ |a|>\Delta ∣a∣>Δ或 ∣ b ∣ > Δ |b|>\Delta ∣b∣>Δ時, [ V ] a , b = 0 [\mathbf{V}]_{a,b}=0 [V]a,b?=0,因而我們可以得到
[ H ] i , j = u + ∑ a = ? Δ Δ ∑ b = ? Δ Δ [ V ] a , b [ X ] i + a , j + b [\mathbf{H}]_{i,j} = u + \sum_{a=-\Delta}^{\Delta}\sum_{b=-\Delta}^{\Delta}{[\mathbf{V}]_{a,b}}{[\mathbf{X}]_{i+a,j+b}} [H]i,j?=u+a=?Δ∑Δ?b=?Δ∑Δ?[V]a,b?[X]i+a,j+b?
上式就是一個卷積層,其中 V \mathbf{V} V被稱為卷積核或卷積層的權重,而卷積神經網絡是包含卷積層的一類特殊的神經網絡。 - 卷積神經網絡相較于多層感知機,參數大幅減小,但代價是圖像特征要求是平移不變的,并且當確定每個隱藏神經元激活值時,每一層只包含局部的信息。
1.2. 卷積層
1.2.1. 圖像卷積
- 卷積運算
- 數學定義: ( f ? g ) ( x ) = ∫ f ( z ) g ( x ? z ) d z (f * g)(\mathbf{x}) = \int f(\mathbf{z}) g(\mathbf{x}-\mathbf{z}) d\mathbf{z} (f?g)(x)=∫f(z)g(x?z)dz
- 針對一維離散對象: ( f ? g ) ( i ) = ∑ a f ( a ) g ( i ? a ) (f * g)(i) = \sum_a f(a) g(i-a) (f?g)(i)=a∑?f(a)g(i?a)
- 針對二維離散對象: ( f ? g ) ( i , j ) = ∑ a ∑ b f ( a , b ) g ( i ? a , j ? b ) (f * g)(i, j) = \sum_a\sum_b f(a, b) g(i-a, j-b) (f?g)(i,j)=a∑?b∑?f(a,b)g(i?a,j?b)
- 上述卷積層所描述的運算使用 ( i + a , j + b ) (i+a,j+b) (i+a,j+b),稱為互相關運算,但這種與卷積運算使用 ( i ? a , j ? b ) (i-a,j-b) (i?a,j?b)的實質是一致的,因為我們總是可以匹配兩種運算之間的符號。
- 在卷積層中,輸入張量和核張量通過互相關運算產生輸出張量。具體過程是卷積核窗口從輸入張量的左上角開始,從左到右、從上到下滑動。 當卷積核窗口滑動到新一個位置時,包含在該窗口中的部分張量與卷積核張量進行按元素相乘,得到的張量再求和得到一個單一的標量值,由此我們得出了這一位置的輸出張量值。
- 卷積層中的兩個被訓練的參數是卷積核權重和標量偏置。
- 要執行嚴格卷積運算,我們只需水平和垂直翻轉二維卷積核張量,然后對輸入張量執行互相關運算。由于卷積核是從數據中學習到的,因此無論這些層執行嚴格的卷積運算還是互相關運算,卷積層的輸出都不會受到影響,以后不加區別統稱卷積運算。
- 由于輸入圖像是三維的,對于每一個空間位置,我們想要采用一組而不是一個隱藏表示。這樣一組隱藏表示可以想象成一些互相堆疊的二維網格。 因此,我們可以把隱藏表示想象為一系列具有二維張量的通道(channel)。這些通道有時也被稱為特征映射(feature maps),因為每個通道都向后續層提供一組空間化的學習特征,可以被視為輸入映射到下一層的空間維度的轉換器。
- 在卷積神經網絡中,對于某一層的任意元素 x x x,其感受野(receptive field)是指在前向傳播期間可能影響 x x x計算的所有元素(來自所有先前層)。當需要檢測輸入特征中更廣區域時,我們可以構建一個更深的卷積網絡。
1.2.2. 填充和步幅
- 卷積的輸出形狀取決于輸入形狀和卷積核的形狀。
- 在應用多層卷積時,我們常常丟失邊緣像素。解決這個問題的簡單方法即為填充(padding),即在輸入圖像的邊界填充元素(通常填充元素是0)。
- 一般在頂部和底部填充相同數量的行,在左側和右側填充相同數量的列。
- 輸入 n h × n w n_h\times n_w nh?×nw?,卷積核 k h × k w k_h\times k_w kh?×kw?,上下分別填充 p h p_h ph?行,左右分別填充 p w p_w pw?列,則輸出 ( n h ? k h + 1 + 2 ? p h ) × ( n w ? k w + 1 + 2 ? p w ) (n_h-k_h+1+2*p_h)\times(n_w-k_w+1+2*p_w) (nh??kh?+1+2?ph?)×(nw??kw?+1+2?pw?)
- 在許多情況下,我們需要設置 p h = ( k h ? 1 ) / 2 p_h=(k_h-1)/2 ph?=(kh??1)/2和 p w = ( k w ? 1 ) / 2 p_w=(k_w-1)/2 pw?=(kw??1)/2,使輸入和輸出具有相同的高度和寬度,這樣可以在構建網絡時更容易地預測每個圖層的輸出形狀。
- 當卷積核的高度和寬度不同時,我們可以填充不同的高度和寬度,使輸出和輸入具有相同的高度和寬度。
- 有時候為了高效計算或是縮減采樣次數,卷積窗口可以跳過中間位置,每次滑動多個元素,每次滑動元素的數量稱為步幅(stride)。
- 輸入 n h × n w n_h\times n_w nh?×nw?,卷積核 k h × k w k_h\times k_w kh?×kw?,上下分別填充 p h p_h ph?行,左右分別填充 p w p_w pw?列,垂直步幅為 s h s_h sh?,水平步幅為 s w s_w sw?,則輸出 ? ( n h ? k h + 2 ? p h + s h ) / s h ? × ? ( n w ? k w + 2 ? p w + s w ) / s w ? \lfloor(n_h-k_h+2*p_h+s_h)/s_h\rfloor\times\lfloor(n_w-k_w+2*p_w+s_w)/s_w\rfloor ?(nh??kh?+2?ph?+sh?)/sh??×?(nw??kw?+2?pw?+sw?)/sw??如果我們設置了 p h = ( k h ? 1 ) / 2 p_h=(k_h-1)/2 ph?=(kh??1)/2和 p w = ( k w ? 1 ) / 2 p_w=(k_w-1)/2 pw?=(kw??1)/2,則輸出 ? ( n h + s h ? 1 ) / s h ? × ? ( n w + s w ? 1 ) / s w ? \lfloor(n_h+s_h-1)/s_h\rfloor\times\lfloor(n_w+s_w-1)/s_w\rfloor ?(nh?+sh??1)/sh??×?(nw?+sw??1)/sw??如果進一步,輸入的高度和寬度可以被垂直和水平步幅整除,則輸出 ( n h / s h ) × ( n w / s w ) (n_h/s_h)\times(n_w/s_w) (nh?/sh?)×(nw?/sw?)
- 為了簡潔起見,輸入高度上下兩側分別為 p h p_h ph?,輸入寬度左右兩側的填充數量分別為 p w p_w pw?時,稱為填充 ( p h , p w ) (p_h,p_w) (ph?,pw?), p h = p w = p p_h=p_w=p ph?=pw?=p時,填充是 p p p;同理,高度和寬度上的步幅分別為 s h s_h sh?和 s w s_w sw?時,稱為步幅 ( s h , s w ) (s_h,s_w) (sh?,sw?), s h = s w = s s_h=s_w=s sh?=sw?=s時,步幅是 s s s。默認情況下,填充為0,步幅為1。在實踐中,我們很少使用不一致的步幅或填充,即總有 p h = p w p_h=p_w ph?=pw?和 s h = s w s_h=s_w sh?=sw?。
1.2.3. 多通道
- 多輸入通道
- 假設輸入的通道數為 c i c_i ci?,那么卷積核的輸入通道數也需要為 c i c_i ci?,如果單通道卷積核的窗口形狀是 k h × k w k_h\times k_w kh?×kw?,那么通道數為 c i c_i ci?的卷積核的窗口形狀為 c i × k h × k w c_i\times k_h\times k_w ci?×kh?×kw?。
- 多通道輸入和多輸入通道卷積核之間進行二維互相關運算可以對每個通道輸入的二維張量和卷積核的二維張量進行互相關運算,再對通道求和得到二維張量。
- 多輸出通道
- 可以將每個通道看作對不同特征的響應,但多輸出通道并不僅是學習多個單通道的檢測器,因為每個通道不是獨立學習的,而是為了共同使用而優化的。
- 假設 c i , c o c_i,c_o ci?,co?分別為輸入輸出通道數, k h , k w k_h,k_w kh?,kw?分別為卷積核的高度和寬度,則為了獲得多個通道的輸出,我們可以為每個輸出通道創建一個形狀為 c i × k h × k w c_i\times k_h\times k_w ci?×kh?×kw?的卷積核張量,這樣卷積核的形狀為 c o × c i × k h × k w c_o\times c_i\times k_h\times k_w co?×ci?×kh?×kw?。在互相關運算中,每個輸出通道先獲取所有輸入通道,再以對應該輸出通道的卷積核計算出結果。
- 1 × 1 1\times1 1×1卷積層
- 失去了卷積層的特有能力——在高度和寬度維度上,識別相鄰元素間相互作用的能力。
- 唯一計算發生在通道上。輸出中的每個元素都是從輸入圖像中同一位置的元素的線性組合。 可以將 1 × 1 1\times1 1×1卷積看作在每個像素位置應用的全連接層。 1 × 1 1\times1 1×1卷積層的權重維度為 c i × c o c_i\times c_o ci?×co?,再額外加上一個偏置。
- 通常用于調整網絡層的通道數量和控制模型復雜性。
1.3. 池化層(又稱匯聚層)
1.3.1. 背景
- 機器學習任務通常會跟全局圖像的問題有關,所以我們最后一層的神經元應該對整個輸入的全局敏感。通過逐漸聚合信息,生成越來越粗糙的映射,最終實現學習全局表示的目標,同時將卷積圖層的所有優勢保留在中間層。
- 池化層的主要作用是降低卷積層對位置的敏感性,同時降低對空間降采樣表示的敏感性。
1.3.2. 池化運算
- 與卷積運算類似, p × q p\times q p×q池化運算使用一個固定形狀為 p × q p\times q p×q的池化窗口,根據其步幅大小在輸入的所有區域上滑動計算相應輸出。
- 池化運算是確定性的,我們通常計算池化窗口中所有元素的最大值或平均值。這些操作分別稱為最大池化(maximum pooling)和平均池化(average pooling)。
1.3.3. 填充和步幅
池化層的填充和步幅與卷積層類似。默認情況下,深度學習框架中的步幅與池化窗口的形狀大小相同。
1.3.4. 多通道
在處理多通道輸入數據時,池化層在每個輸入通道上單獨運算,而不是像卷積層一樣在通道上對輸入進行匯總。 這意味著池化層的輸出通道數與輸入通道數相同。
1.4. 卷積神經網絡(LeNet)
1.4.1. 簡介
- LeNet是最早發布的卷積神經網絡之一,由AT&T貝爾實驗室的研究員Yann LeCun在1989年提出的(并以其命名),目的是識別圖像中的手寫數字。
- Yann LeCun發表了第一篇通過反向傳播成功訓練卷積神經網絡的研究,這項工作代表了十多年來神經網絡研究開發的成果。
- LeNet被廣泛用于自動取款機(ATM)機中,幫助識別處理支票的數字。
1.4.2. 組成
- 總體來看,LeNet(LeNet-5)由兩個部分組成:
- 卷積編碼器:由兩個卷積層組成;
- 全連接層密集塊:由三個全連接層組成。

- 數據維度變化
卷積層數據維度表示:(樣本數,通道數,高度,寬度);
展平層、全連接層輸出數據維度表示:(樣本數,輸出數)。位置 數據維度 輸入數據 28 x 28 (C1) 5 × 5 5\times5 5×5卷積層(填充2)輸入 1 x 1 x 28 x 28 (C1) 5 × 5 5\times5 5×5卷積層(填充2)輸出 1 x 6 x 28 x 28 Sigmoid激活函數輸出 1 x 6 x 28 x 28 (S2) 2 × 2 2\times2 2×2平均池化層(步幅2)輸出 1 x 6 x 14 x 14 (C3) 5 × 5 5\times5 5×5卷積層輸入 1 x 6 x 10 x 10 (C3) 5 × 5 5\times5 5×5卷積層輸出 1 x 16 x 10 x 10 Sigmoid激活函數輸出 1 x 16 x 10 x 10 (S4) 2 × 2 2\times2 2×2平均池化層輸出 1 x 16 x 5 x 5 展平層輸出 1 x 400 (120-F5)全連接層輸出 1 x 120 Sigmoid激活函數輸出 1 x 120 (84-F6)全連接層輸出 1 x 84 Sigmoid激活函數輸出 1 x 84 輸出結果 1 x 10
2. 實例解析
2.1. 實例描述
- 圖像中目標的邊緣檢測
構造一個 6 × 8 6\times8 6×8像素的黑白圖像,中間四列為黑色(0),其余像素為白色(1)。要求進行邊緣檢測,輸出中的1代表從白色到黑色的邊緣,-1代表從黑色到白色的邊緣,其他情況的輸出為0。 - 在FashionMNIST數據集上訓練LeNet
2.2. 代碼實現
2.2.1. 圖像中目標的邊緣檢測
2.2.1.1. 主要代碼
net = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)
2.2.1.2. 完整代碼
import torch
from torch import nn
from torch.nn import functional as Fif __name__ == '__main__':# 全局參數設置lr = 3e-2num_epochs = 10# 生成數據集X = torch.ones(6, 8)X[:, 2:6] = 0Y = torch.zeros(6, 7)Y[:, 1], Y[:, 5] = 1, -1# 批數、通道數、高度、寬度X = X.reshape(1, 1, 6, 8)Y = Y.reshape(1, 1, 6, 7)print('1. 使用邊緣檢測器(1, -1)')K = torch.tensor([1.0, -1.0]).reshape(1, 1, 1, 2)O = F.conv2d(X, K, bias=None)print(f'邊緣檢測器的結果O與標準結果Y是否相同:{O.equal(Y)}')print('2. 學習卷積核')net = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)# 訓練循環for epoch in range(num_epochs):loss = (net(X) - Y) ** 2 # 平方誤差net.zero_grad()loss.sum().backward()net.weight.data[:] -= lr * net.weight.grad # 參數更新print(f'epoch {epoch + 1}, loss {loss.sum():.3f}')print(f'卷積核權重:{net.weight.data.reshape(1, 2)}')
2.2.1.3. 輸出結果
1. 使用邊緣檢測器(1, -1)
邊緣檢測器的結果O與標準結果Y是否相同:True
2. 學習卷積核
epoch 1, loss 10.272
epoch 2, loss 4.320
epoch 3, loss 1.842
epoch 4, loss 0.801
epoch 5, loss 0.358
epoch 6, loss 0.165
epoch 7, loss 0.080
epoch 8, loss 0.040
epoch 9, loss 0.022
epoch 10, loss 0.012
卷積核權重:tensor([[ 0.9799, -0.9993]])
2.2.2. 在FashionMNIST數據集上訓練LeNet
2.2.2.1. 主要代碼
LeNet = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Flatten(),nn.Linear(400, 120), nn.Sigmoid(),nn.Linear(120, 84), nn.Sigmoid(),nn.Linear(84, 10)
).to(device)
2.2.2.2. 完整代碼
import torch, os
from torch import nn, optim
from torch.utils.data import DataLoader
from torchvision.transforms import Compose, ToTensor, Resize
from torchvision.datasets import FashionMNIST
from tensorboardX import SummaryWriter
from rich.progress import trackdef load_dataset():"""加載數據集"""root = "./dataset"transform = Compose([ToTensor()])mnist_train = FashionMNIST(root, True, transform, download=True)mnist_test = FashionMNIST(root, False, transform, download=True)dataloader_train = DataLoader(mnist_train, batch_size, shuffle=True, num_workers=num_workers,)dataloader_test = DataLoader(mnist_test, batch_size, shuffle=False,num_workers=num_workers,)return dataloader_train, dataloader_testif __name__ == "__main__":# 全局參數設置num_epochs = 100batch_size = 256num_workers = 3lr = 0.9device = torch.device('cuda')# 創建記錄器def log_dir():root = "runs"if not os.path.exists(root):os.mkdir(root)order = len(os.listdir(root)) + 1return f'{root}/exp{order}'writer = SummaryWriter(log_dir=log_dir())# 數據集配置dataloader_train, dataloader_test = load_dataset()# 模型配置LeNet = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Flatten(),nn.Linear(400, 120), nn.Sigmoid(),nn.Linear(120, 84), nn.Sigmoid(),nn.Linear(84, 10)).to(device)def init_weights(m):if type(m) == nn.Linear or type(m) == nn.Conv2d:nn.init.xavier_uniform_(m.weight)LeNet.apply(init_weights)criterion = nn.CrossEntropyLoss(reduction='none')optimizer = optim.SGD(LeNet.parameters(), lr=lr)# 訓練循環for epoch in track(range(num_epochs), description='LeNet'):LeNet.train()for X, y in dataloader_train:X, y = X.to(device), y.to(device)optimizer.zero_grad()loss = criterion(LeNet(X), y)loss.mean().backward()optimizer.step()LeNet.eval()with torch.no_grad():train_loss, train_acc, num_samples = 0.0, 0.0, 0for X, y in dataloader_train:X, y = X.to(device), y.to(device)y_hat = LeNet(X)loss = criterion(y_hat, y)train_loss += loss.sum()train_acc += (y_hat.argmax(dim=1) == y).sum()num_samples += y.numel()train_loss /= num_samplestrain_acc /= num_samplestest_acc, num_samples = 0.0, 0for X, y in dataloader_test:X, y = X.to(device), y.to(device)y_hat = LeNet(X)test_acc += (y_hat.argmax(dim=1) == y).sum()num_samples += y.numel()test_acc /= num_sampleswriter.add_scalars('metrics', {'train_loss': train_loss,'train_acc': train_acc,'test_acc': test_acc}, epoch)writer.close()
2.2.2.3. 輸出結果
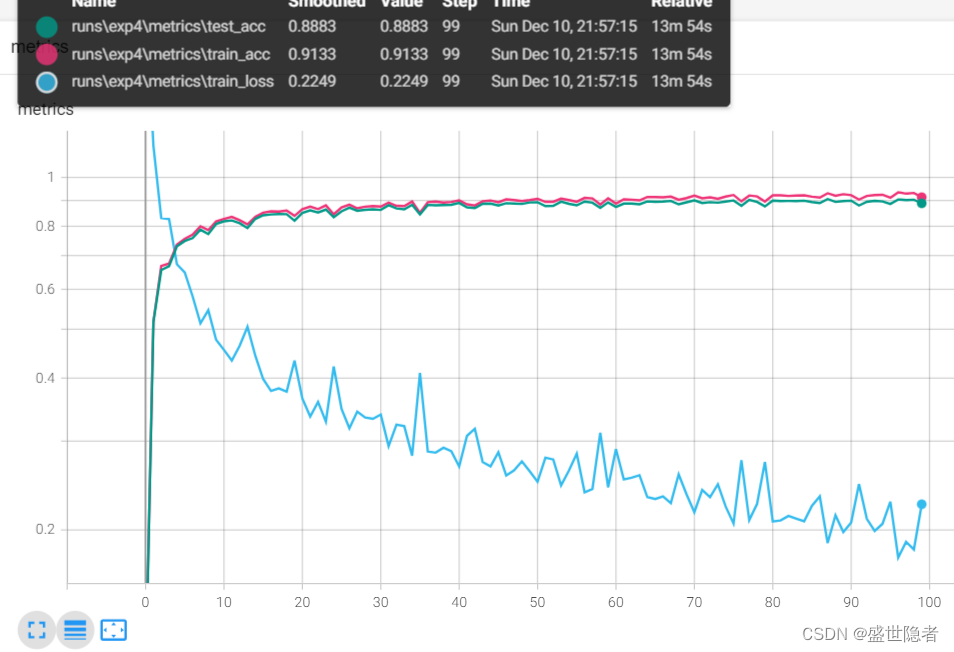

))







)








基本介紹、快速入門)
