學習目標：

動態規劃五部曲：
① 確定dp[i]的含義
② 求遞推公式
③ dp數組如何初始化
④ 確定遍歷順序
⑤ 打印遞歸數組 ---- 調試
引用自代碼隨想錄！

本文大多數內容引用自代碼隨想錄

60天訓練營打卡計劃！

學習內容：

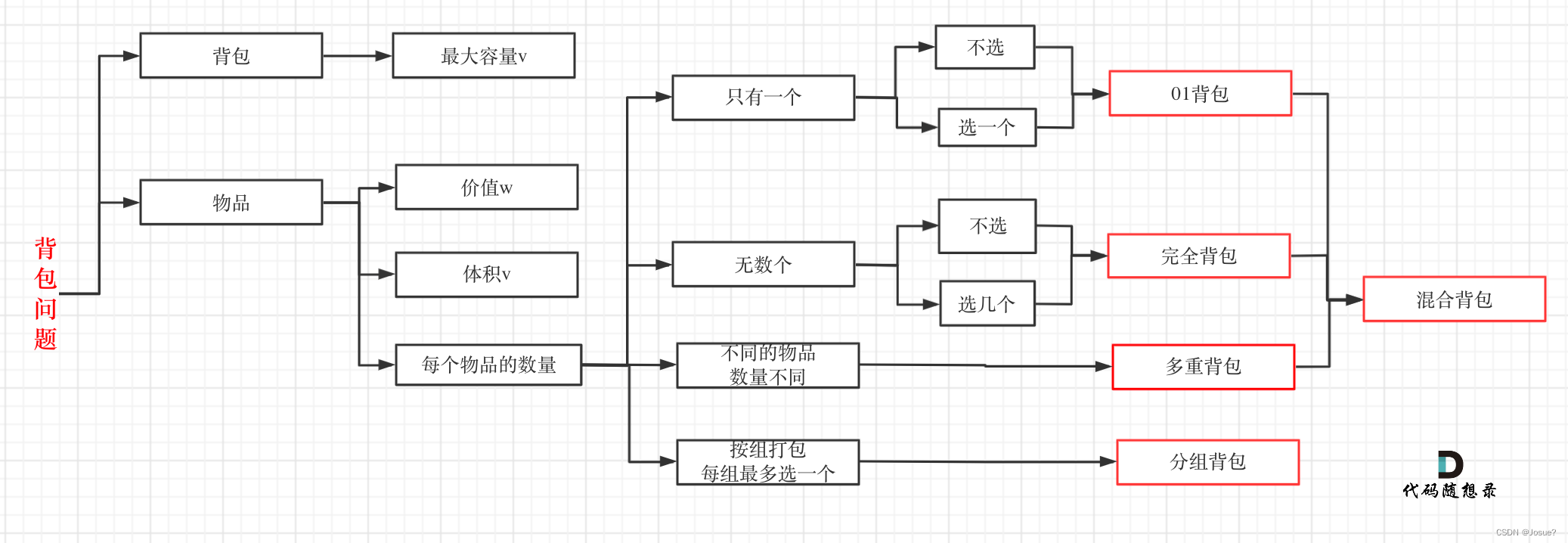
上述內容引用自代碼隨想錄

• 使用動歸五部曲分析題目，見過的題目就可以被輕松帶走。最重要的就是dp[]數組的含義，遞歸函數即遍歷的順序。

1.背包遞推公式

問能否能裝滿背包（或者最多裝多少）：
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ，對應題目如下：

• 動態規劃：416.分割等和子集
• 動態規劃：1049.最后一塊石頭的重量 II
• 動態規劃：139.單詞拆分

問裝滿背包有幾種方法：dp[j] += dp[j - nums[i]] ，對應題目如下：

• 動態規劃：494.目標和
• 動態規劃：518. 零錢兌換 II
• 動態規劃：377.組合總和Ⅳ
• 動態規劃：70. 爬樓梯進階版（完全背包）

問背包裝滿最大價值：
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，對應題目如下：

• 動態規劃：474.一和零

問裝滿背包所有物品的最小個數：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ，對應題目如下：

• 動態規劃：322.零錢兌換
• 動態規劃：279.完全平方數

2.遍歷順序

01背包

二維dp數組01背包先遍歷物品還是先遍歷背包都是可以的，且第二層for循環是從小到大遍歷。一維dp數組01背包只能先遍歷物品再遍歷背包容量，且第二層for循環是從大到小遍歷。

完全背包

說完01背包，再看看完全背包。

一維dp數組實現，先遍歷物品還是先遍歷背包都是可以的，且第二層for循環是從小到大遍歷。但是僅僅是純完全背包的遍歷順序是這樣的，題目稍有變化，兩個for循環的先后順序就不一樣了。

如果求組合數就是外層for循環遍歷物品，內層for遍歷背包。
如果求排列數就是外層for遍歷背包，內層for循環遍歷物品。

相關題目如下：

求組合數：

• 動態規劃：518.零錢兌換II

求排列數：

• 動態規劃：377. 組合總和 Ⅳ
• 動態規劃：70. 爬樓梯進階版（完全背包）

如果求最小數，那么兩層for循環的先后順序就無所謂了，相關題目如下：
求最小數：

• 動態規劃：322. 零錢兌換
• 動態規劃：279.完全平方數

對于背包問題，其實遞推公式算是容易的，難是難在遍歷順序上，如果把遍歷順序搞透，才算是真正理解了。

---

學習時間：

• 上午兩個半小時，整理文檔半小時。