來源：https://www.bilibili.com/video/BV1Bb4y1L7FT?p=4&vd_source=f66cebc7ed6819c67fca9b4fa3785d39

文章目錄

• 概述
• seq2seq
• transformer
• • Encoder
  • Decoder
  • • Autoregressive（AT）
    • • self-attention與masked-self attention
      • model如何決定輸出的長度
      • Cross-attention——連接encoder和decoder的橋梁
      • Training
      • 評估指標的優化
    • Non-autoregressive（NAT）

概述

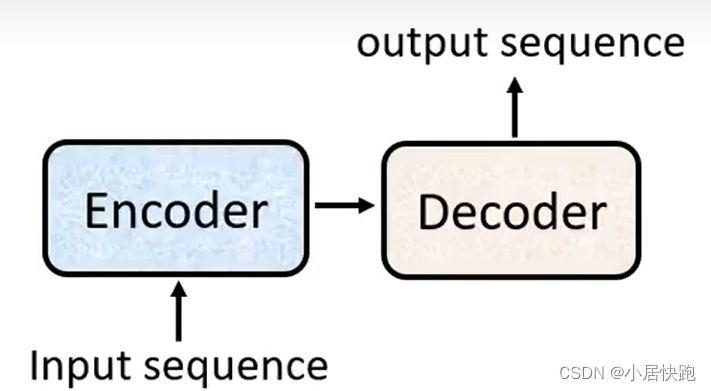
transformer就是一個seq2seq的model。
Input一個sequence，output的長度由機器自己決定。

seq2seq

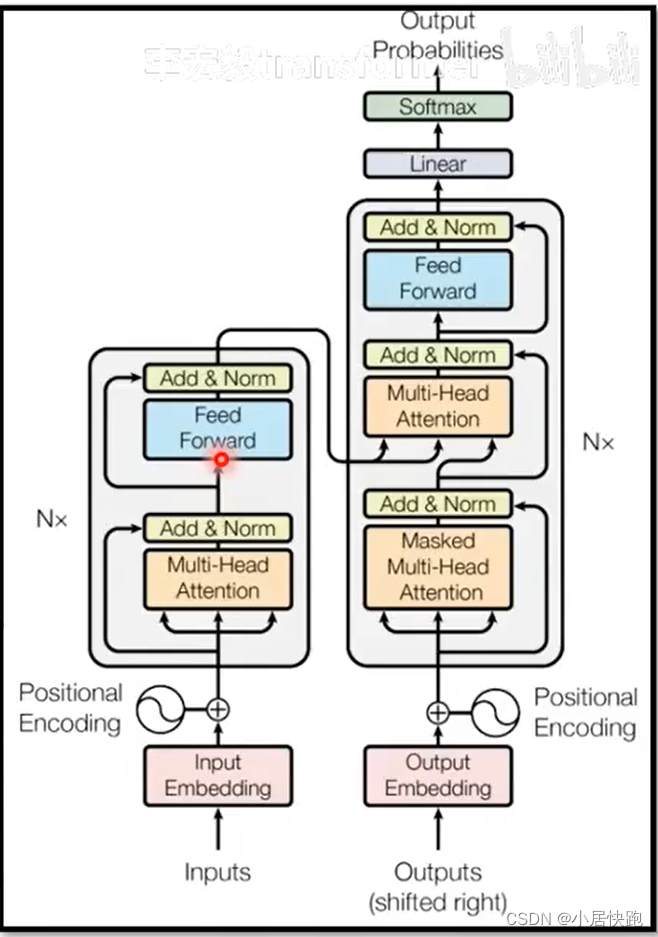
transformer

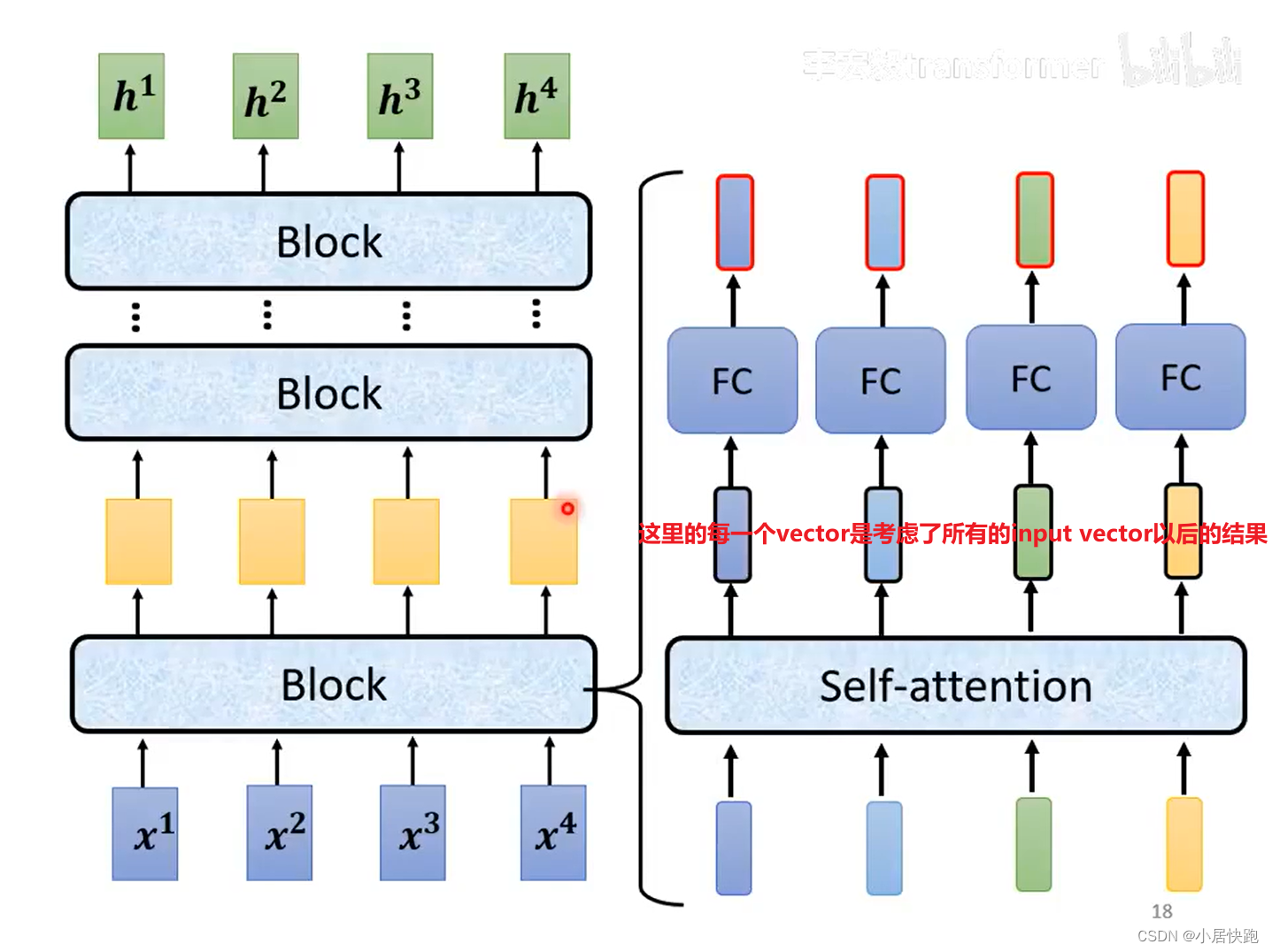
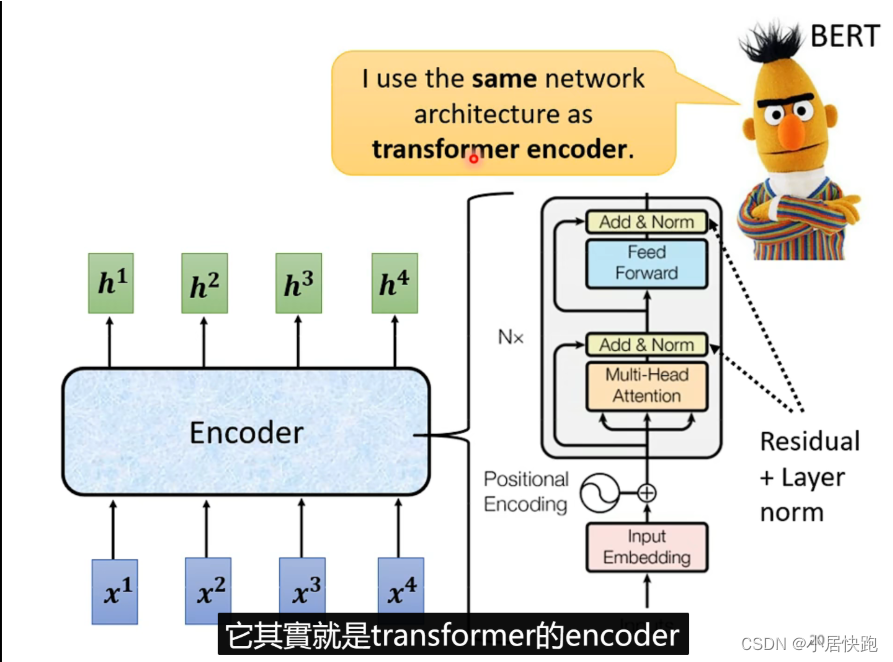
Encoder

輸入一排向量，輸出同樣長度的另一排向量。
每一個Block做的事情是好幾個layer做的事情。
每個block做的事（簡化版）：

完整版：

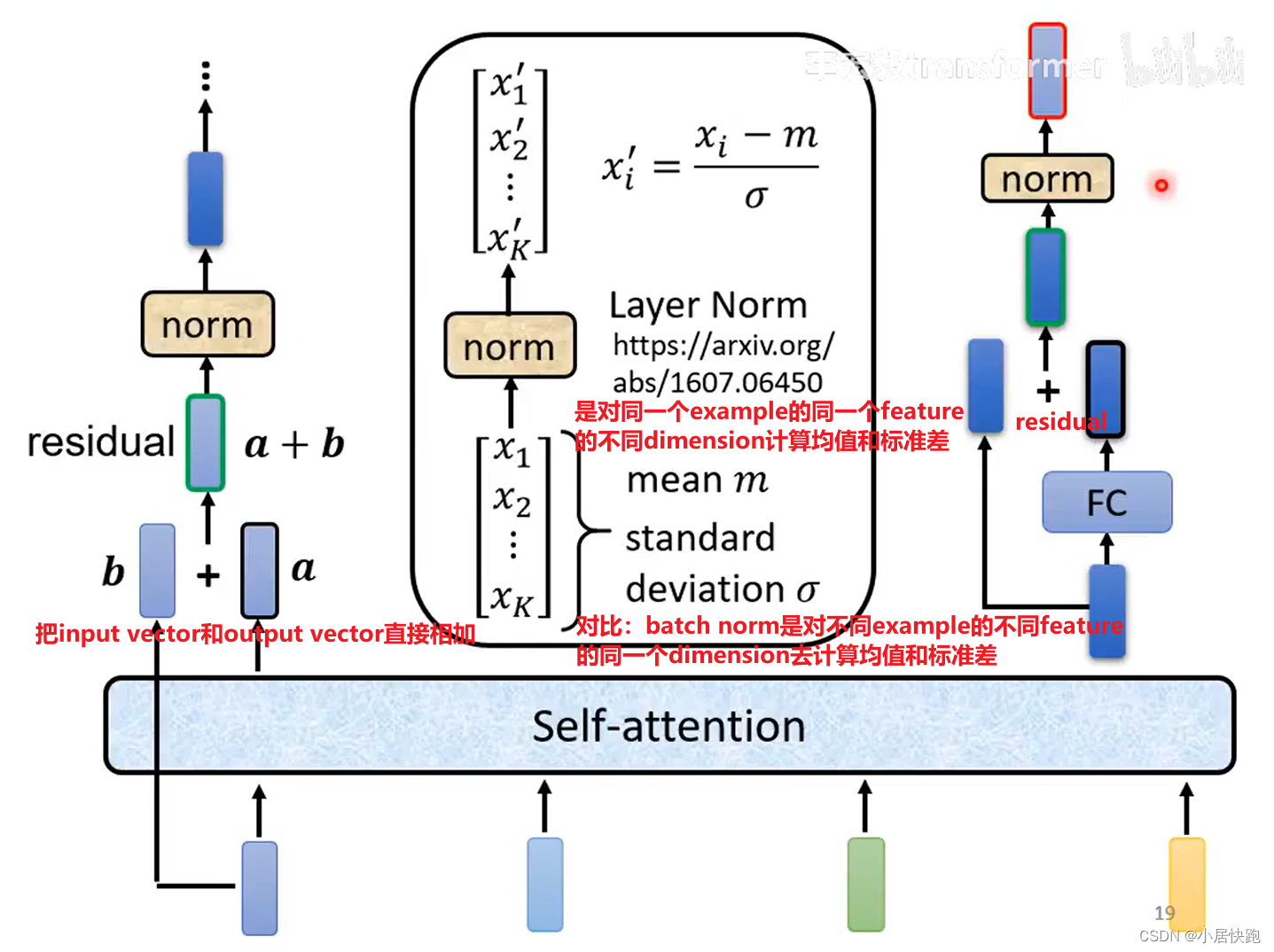
位置的資訊
Bert里會用到同樣的架構：

Decoder

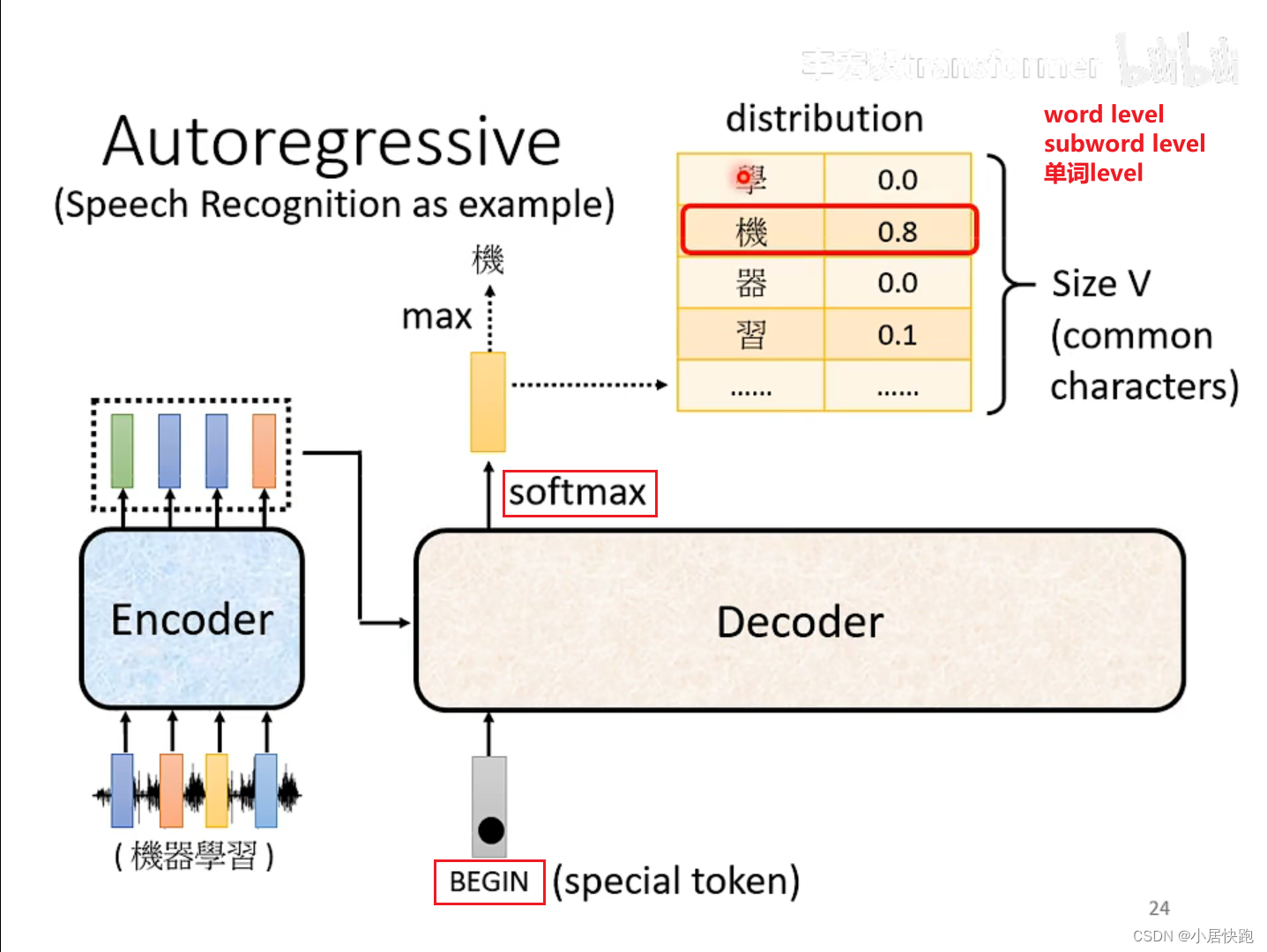
Autoregressive（AT）

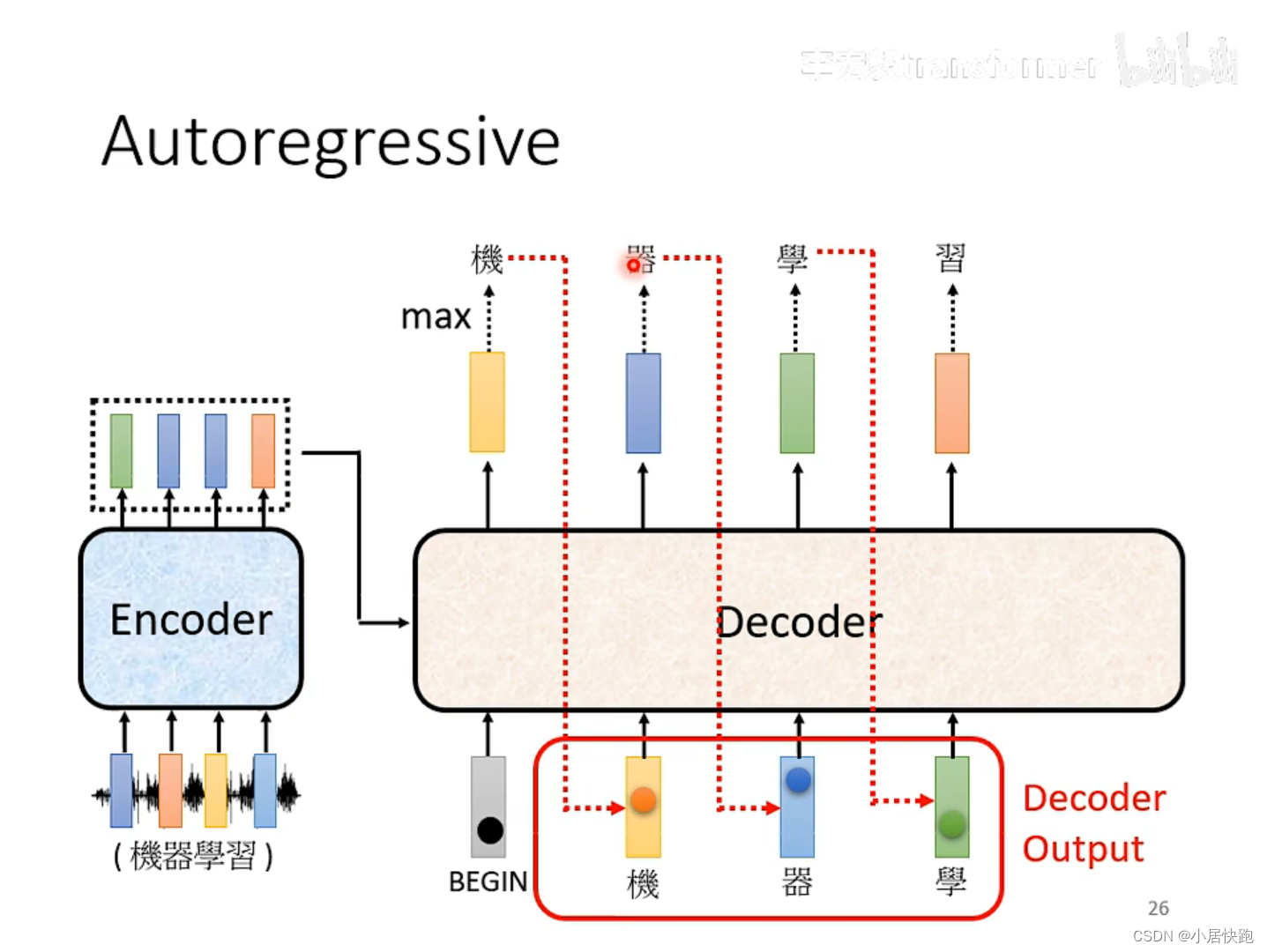
decoder看到的輸入是前一個階段自己的輸出。
那么這樣會不會導致error propagation（一步錯步步錯）？
不會。
exposure bias：test時decoder可能會看到錯誤的輸入，而train時decoder看到的是完全正確的，即它在訓練時完全沒有看過錯誤的東西。
解決方法：scheduled sampling：訓練時給decoder的輸入加一些錯誤的東西。

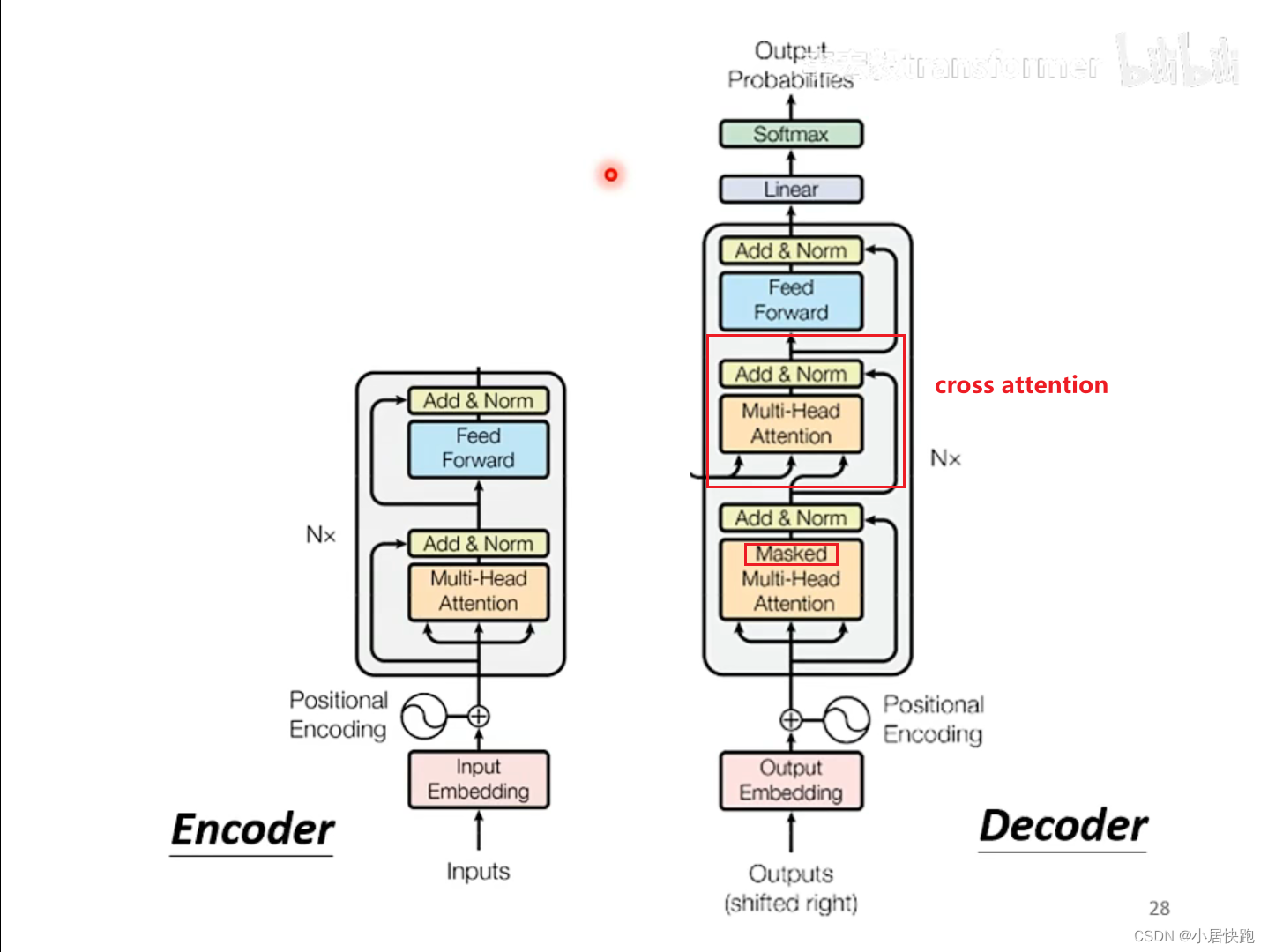
self-attention與masked-self attention

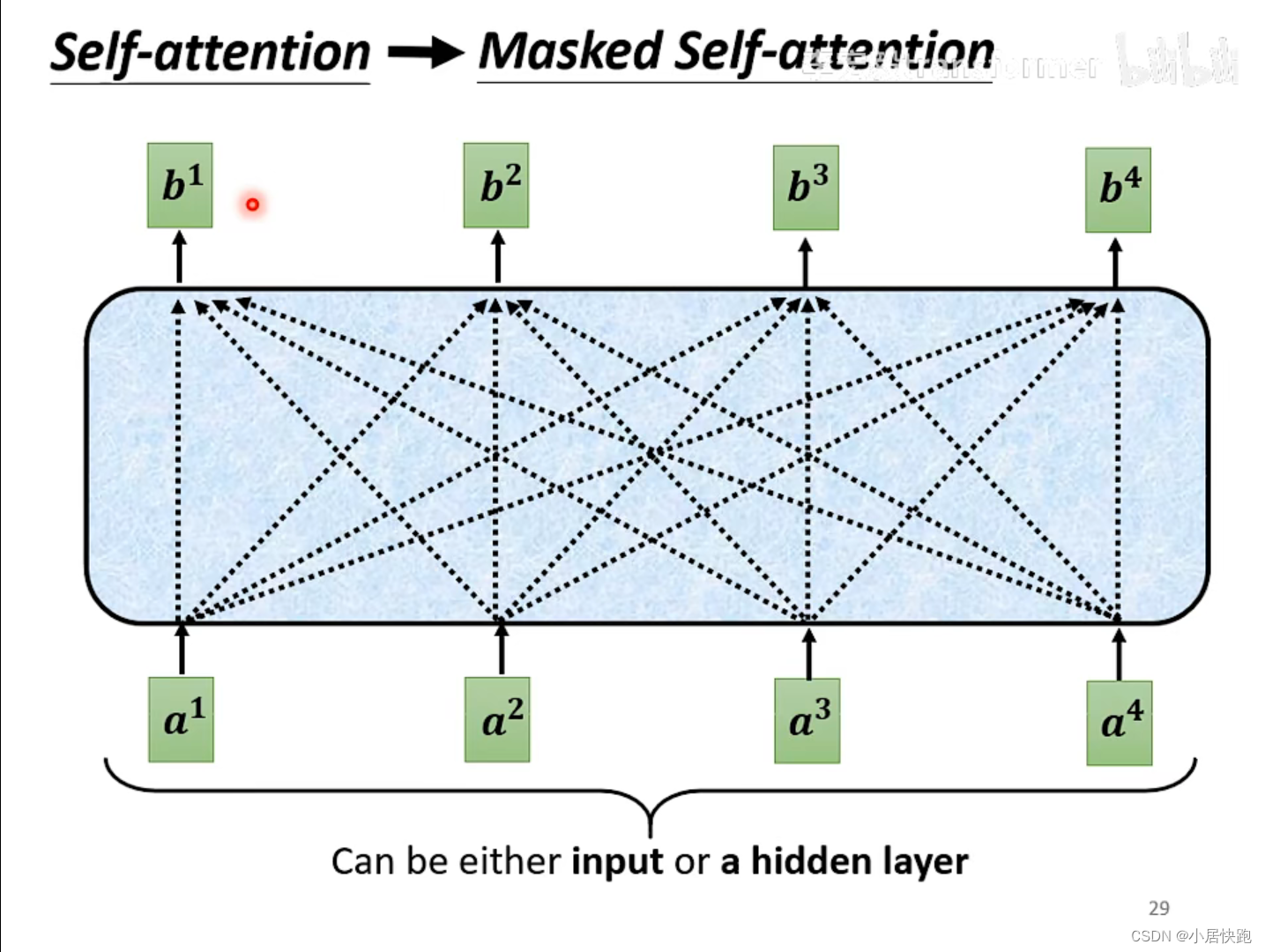
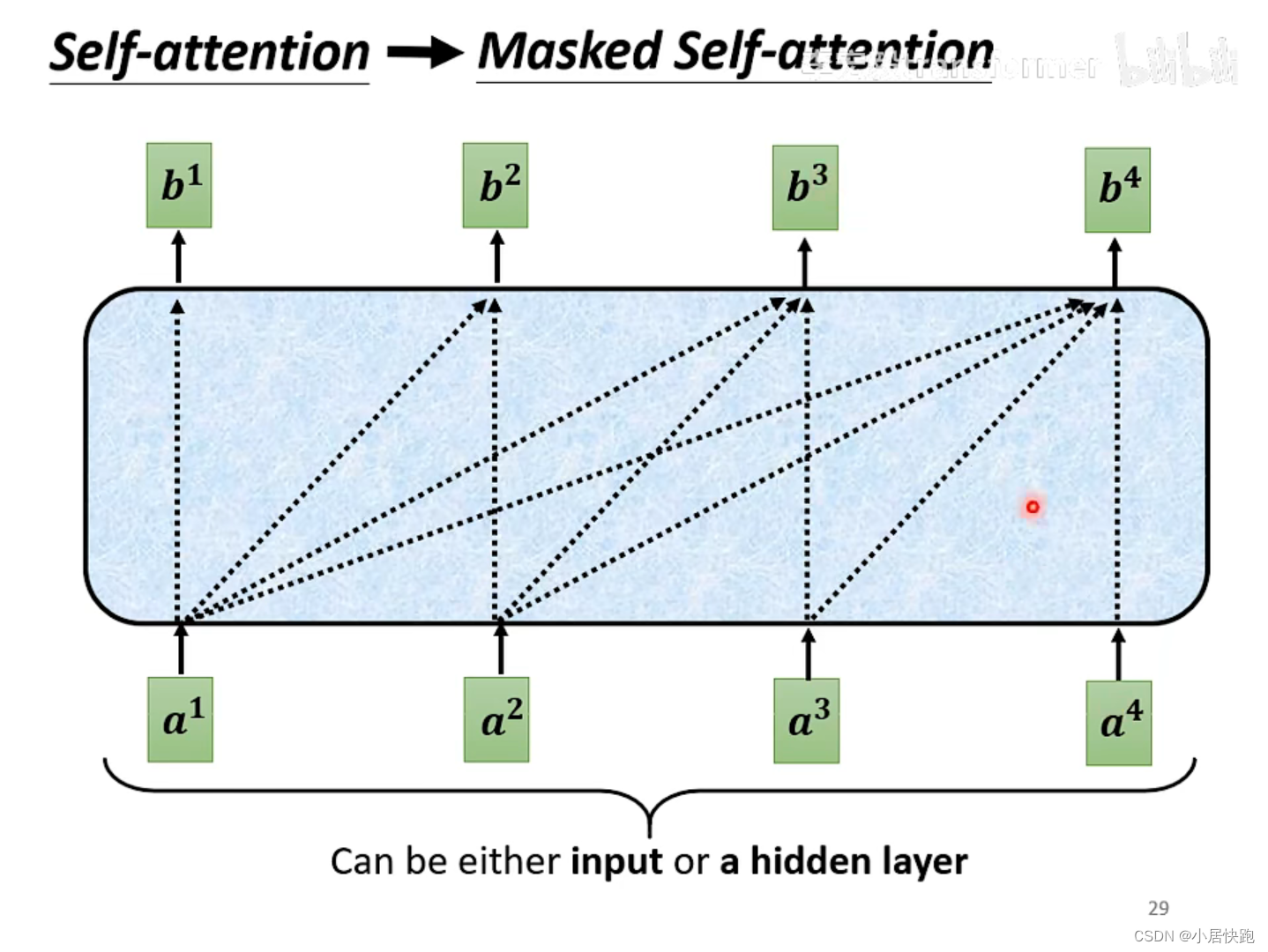
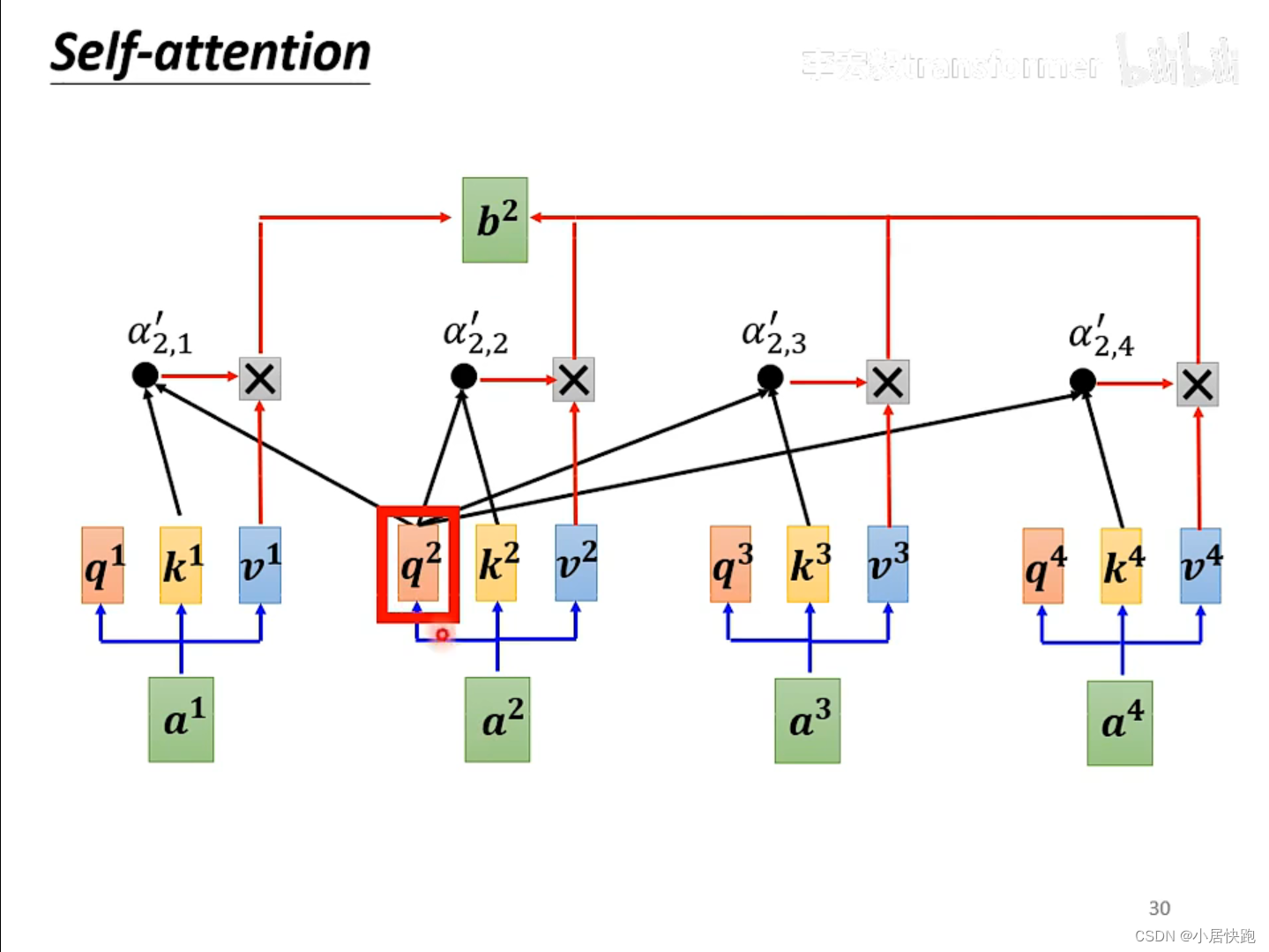
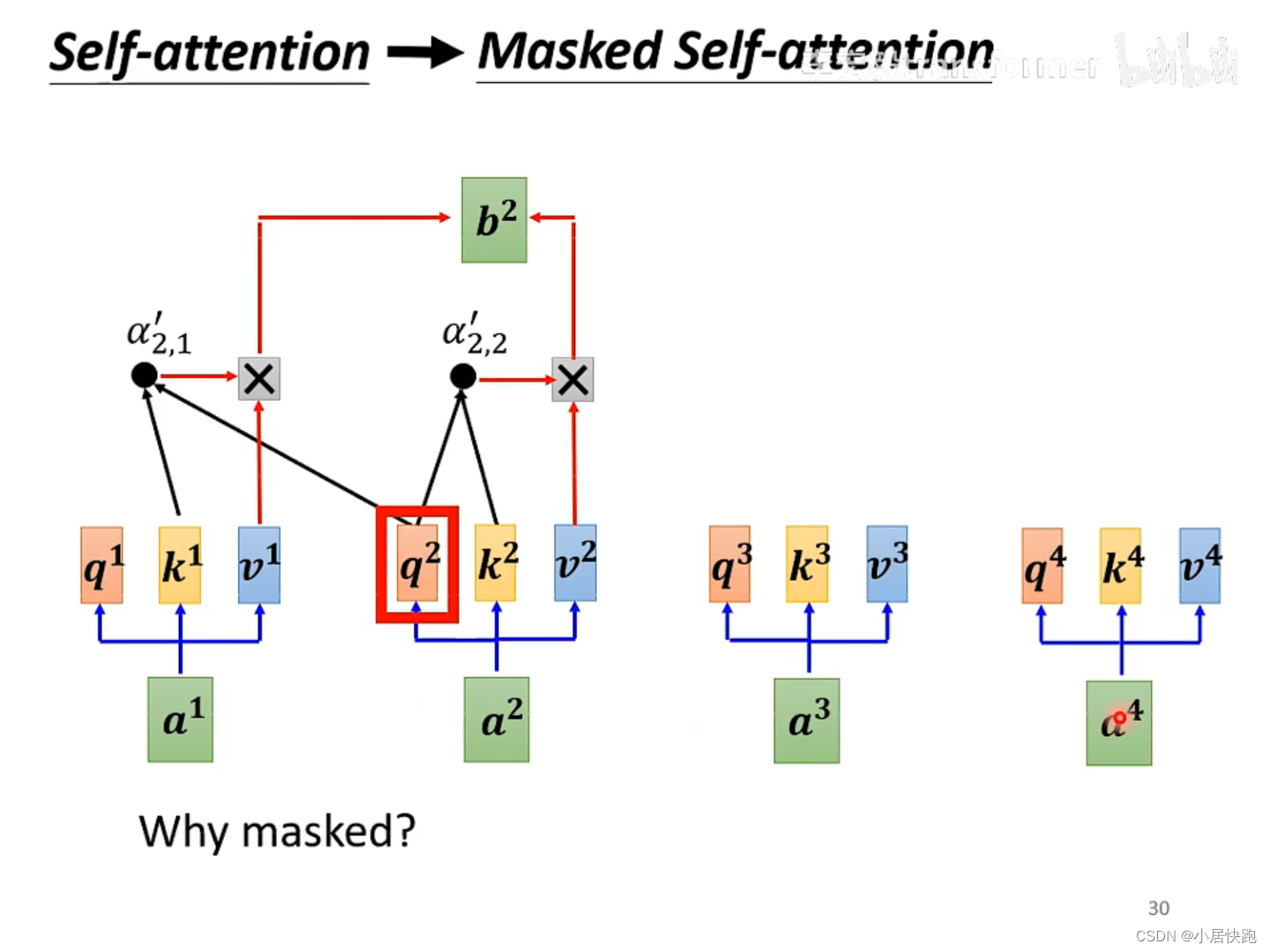
為什么要masked？
因為在encoder里面，input是同時輸進去的；而decoder里面，input是一個一個輸進去的。

model如何決定輸出的長度

加上一個Stop Token
除了所有的中文字、< begin >之外，還需要準備一個< end >，不過通常< begin >和< end >會用同一個符號，因為他們分別只會在開頭和結尾出現。

Cross-attention——連接encoder和decoder的橋梁

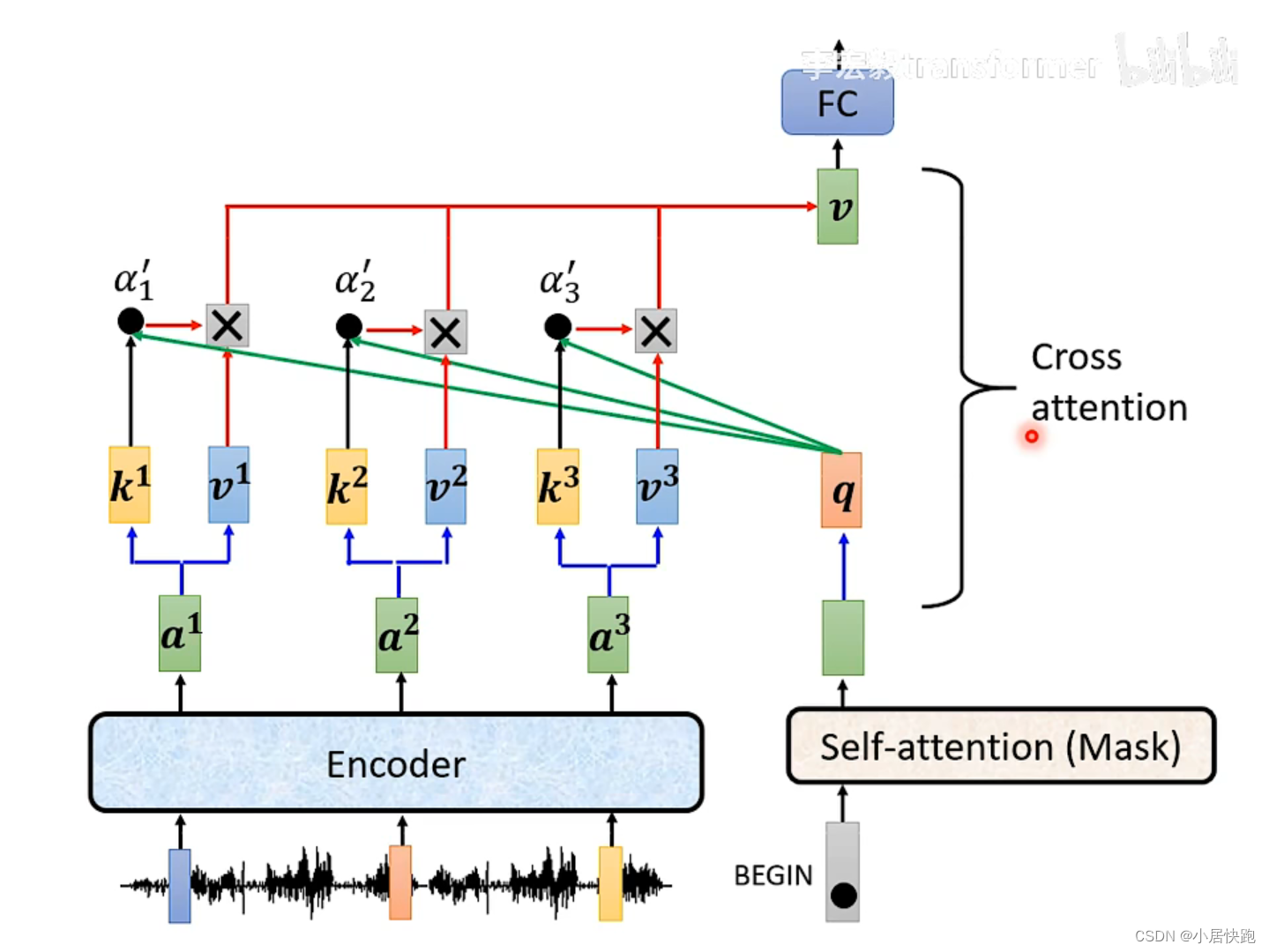
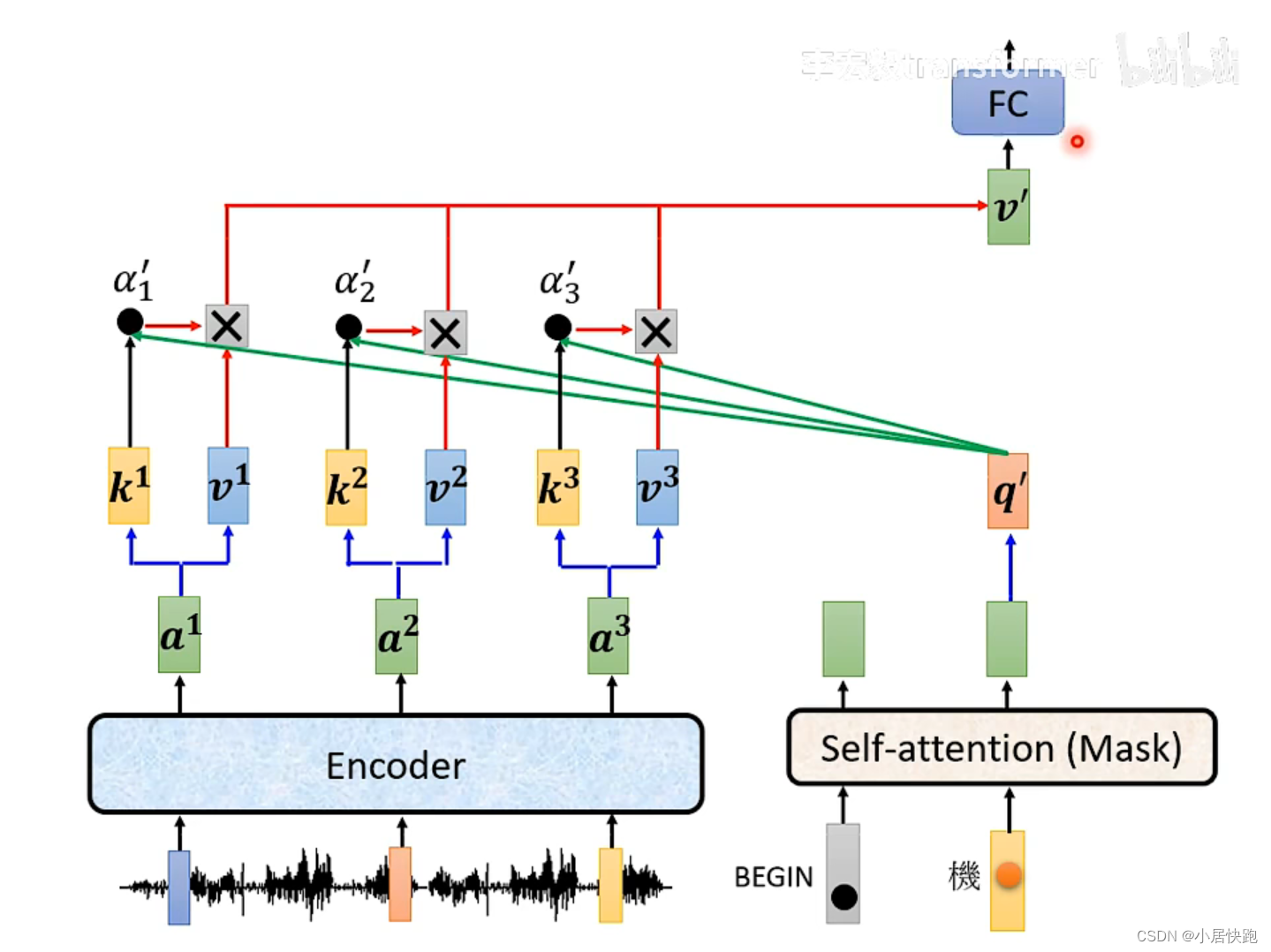
k、v、q如何得出：self-attention|李宏毅機器學習21年

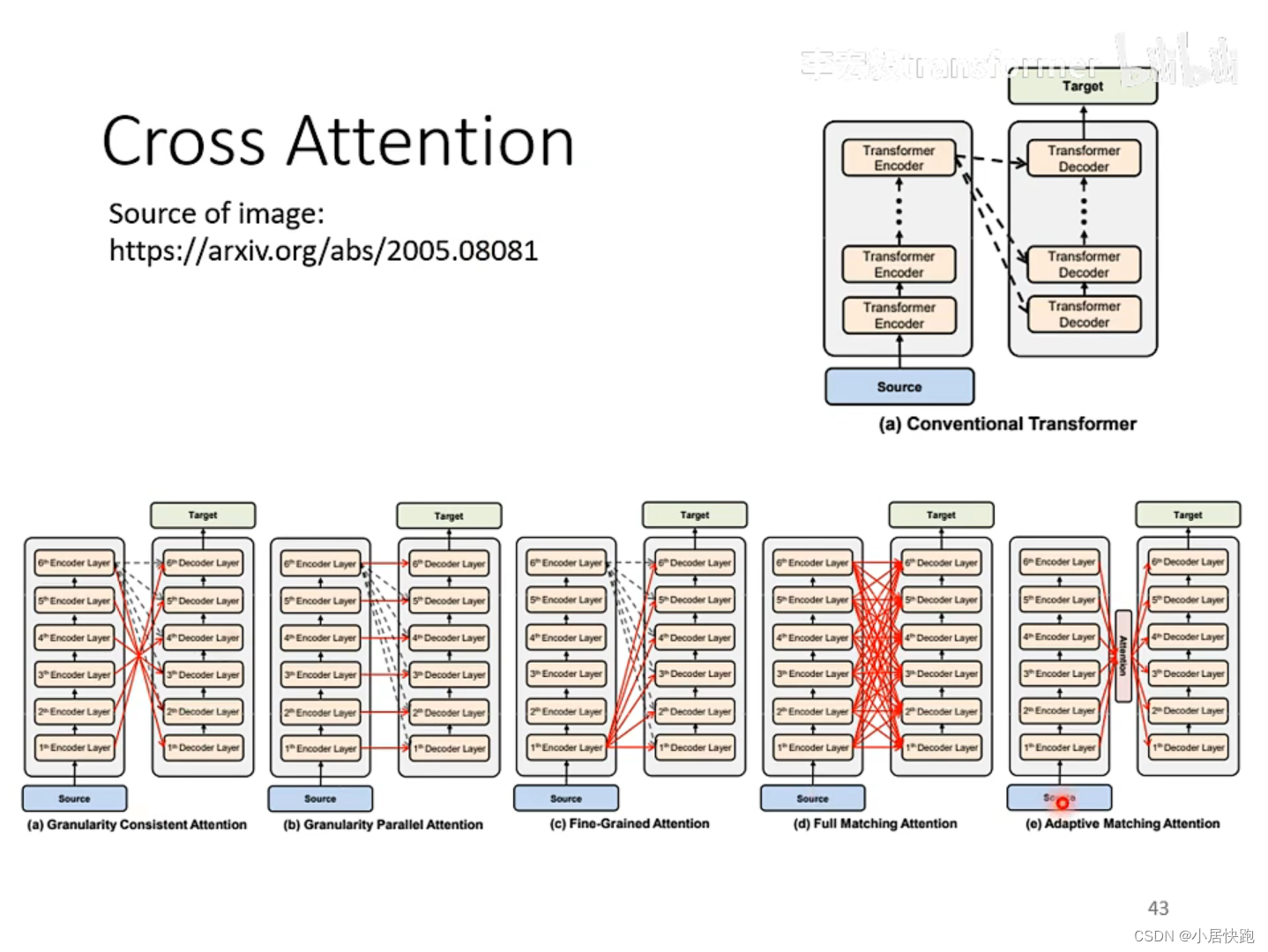
各式各樣的連接方式都可以：

Training

前面的部分都是，假設model訓練好以后，它是怎么做inference的。
訓練資料：輸入-輸出對

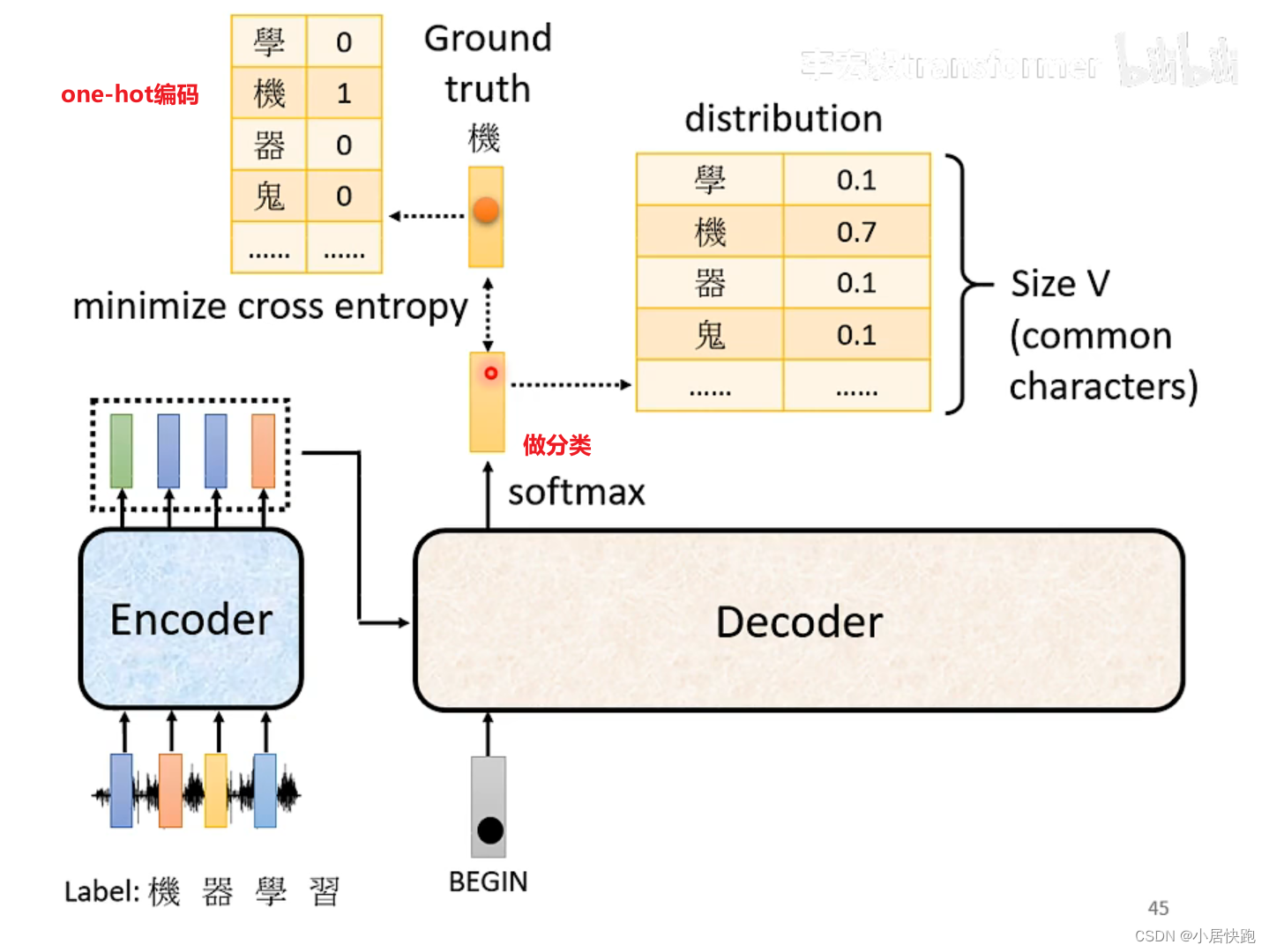
Teacher Forcing：在decoder訓練的時候輸入的是正確答案

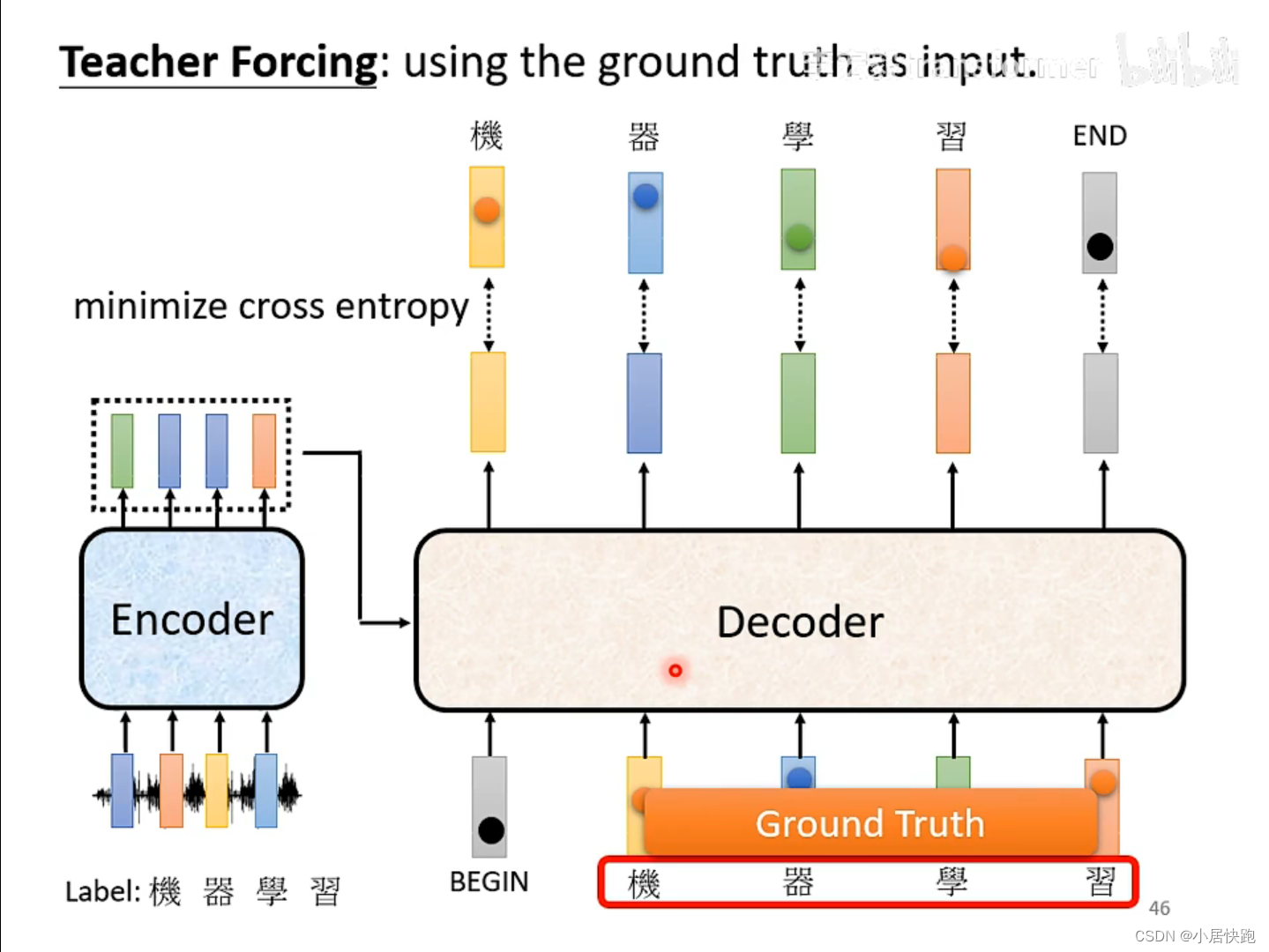
交叉熵（Cross Entropy）是衡量兩個概率分布之間差異的一種度量方式，在機器學習中常用作分類問題的損失函數。假設我們有兩個概率分布的向量，一個是真實的概率分布 $P$，一個是預測的概率分布 $Q$，那么交叉熵可以表示為：
$$H(P,Q)=?\sum _{i}P(i)\log Q(i)$$

舉例：

• 真實概率分布 $P=[0.6,0.4]$
• 預測概率分布 $Q=[0.8,0.2]$
  計算這兩個向量的交叉熵如下：
  $$H(P,Q)=?(0.6\times \log (0.8)+0.4\times \log (0.2))=0.7777$$
  所以這兩個向量的交叉熵大約是 $0.7777$。
  注意，由于交叉熵是衡量兩個分布之間的差異，因此 $P$ 、$Q$必須是有效的概率分布，即 $P$ 、$Q$中的所有元素都必須是非負的，并且它們的和為 1。在實際應用中，為了防止對數函數中出現對零取對數的情況，通常會給 $Q$ 中的元素加上一個很小的正數，比如 $1e?9$。

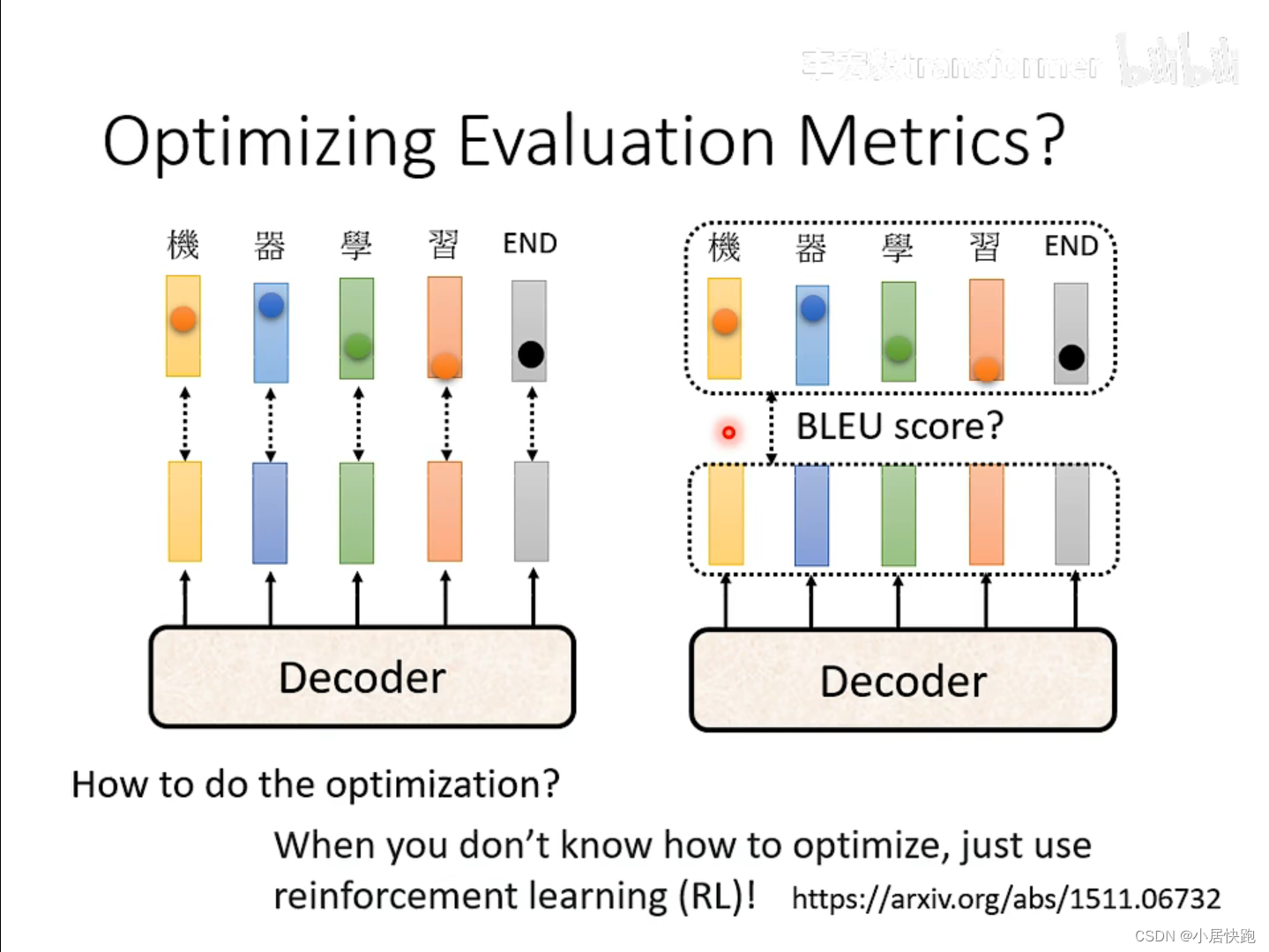
評估指標的優化

訓練時是min cross entropy（字與字之間），測試時是max BLEU score（句子與句子之間），這兩個指標可以等價嗎？
不見得。
訓練的時候都是一個字一個字出來的，怎么在訓練的時候就用BLEU score：
遇到無法optimize的loss fuction，用RL硬train一發就可以。
把fuction當做是RL的reward，把decoder當做agent。（比較難）

BLEU（Bilingual Evaluation Understudy）分數是一種常用于評估機器翻譯質量的指標，它通過比較機器翻譯的文本和一個或多個參考翻譯來計算分數。BLEU分數考慮了準確性（通過n-gram匹配）和流暢性（通過句子長度的懲罰）。

BLEU分數的計算包括以下幾個步驟：

1. n-gram精確度：對于每個n-gram（n可以是1, 2, 3, …），計算機器翻譯中n-gram出現的次數，并與參考翻譯中的n-gram出現次數進行比較。對于每個n-gram，計算其精確度（precision）。

2. 修剪（Clipping）：如果機器翻譯中的n-gram出現次數超過參考翻譯中的最大出現次數，將其修剪至該最大值。

3. 加權平均：對于不同的n-gram精確度，計算它們的幾何平均值，并對結果取自然對數。

4. 句子長度懲罰（Brevity Penalty, BP）：如果機器翻譯的長度小于參考翻譯的長度，將施加一個懲罰以避免過短的翻譯。

計算公式：

$$\text{BLEU}=\text{BP}?\exp \left(\sum _{n=1}^N{w}_n\log p_n\right)$$

其中：

• $p_n$ 是第n個n-gram的精確度。
• $w_n$ 是第n個n-gram的權重，通常取為 $1/N$，使得所有n-gram權重之和為1。
• $\text{BP}$ 是句子長度懲罰，計算方式為：

$$\text{BP}=\{\begin{array}{ll}1& \text{如果機器翻譯的長度}>\text{參考翻譯的長度}\\ \exp \left(1?\frac{\text{參考翻譯的長度}}{\text{機器翻譯的長度}}\right)& \text{其他情況}\end{array}$$

舉例：

本例中機器翻譯（MT）與參考翻譯（Ref）不完全匹配，并且將計算最多包括2-gram的BLEU分數。

假設機器翻譯（MT）為：“the black cat sat on the mat”，參考翻譯（Ref）為：“the cat sat on the mat”。我們計算1-gram和2-gram的BLEU分數（即N=2）。

1. 對于1-gram：

   • MT中的詞：“the”, “black”, “cat”, “sat”, “on”, “the”, “mat”
   • Ref中的詞：“the”, “cat”, “sat”, “on”, “the”, “mat”
   • MT中每個詞的出現次數與Ref中相同或更多的詞有：“the” (2次), “cat” (1次), “sat” (1次), “on” (1次), “mat” (1次)
   • 因此，1-gram精確度 $p_1=\frac{6}{7}$（因為MT中有7個詞，其中6個詞匹配到了Ref）

2. 對于2-gram：

   • MT中的2-gram：“the black”, “black cat”, “cat sat”, “sat on”, “on the”, “the mat”
   • Ref中的2-gram：“the cat”, “cat sat”, “sat on”, “on the mat”
   • MT中每個2-gram的出現次數與Ref中相同或更多的2-gram有：“cat sat” (1次), “sat on” (1次), “on the” (1次)
   • 因此，2-gram精確度 $p_2=\frac{3}{6}$（因為MT中有6個2-gram，其中3個匹配到了Ref）

3. 長度懲罰（BP）：

   • MT的長度為7，Ref的長度為6。
   • 因為MT的長度大于Ref的長度，所以沒有長度懲罰，$\text{BP}=1$。

4. 加權平均：

   • 假設我們給1-gram和2-gram相同的權重，即 $w_1=w_2=0.5$。
   • 加權平均為 $\exp (0.5?\log p_1+0.5?\log p_2)$。

現在我們可以計算BLEU分數：

$$\text{BLEU}=\text{BP}?\exp \left(0.5?\log \frac{6}{7}+0.5?\log \frac{3}{6}\right)$$

計算具體數值：

$$\text{BLEU}=1?\exp \left(0.5?\log \frac{6}{7}+0.5?\log \frac{1}{2}\right)$$
$$\text{BLEU}\approx \exp \left(?0.42365\right)\approx 0.65468$$
因此，BLEU分數大約為0.65468。這個分數反映了機器翻譯與參考翻譯在1-gram和2-gram層面上的部分匹配程度。在實際應用中，BLEU分數通常會乘以100，因此這個分數可能會表示為65.468。

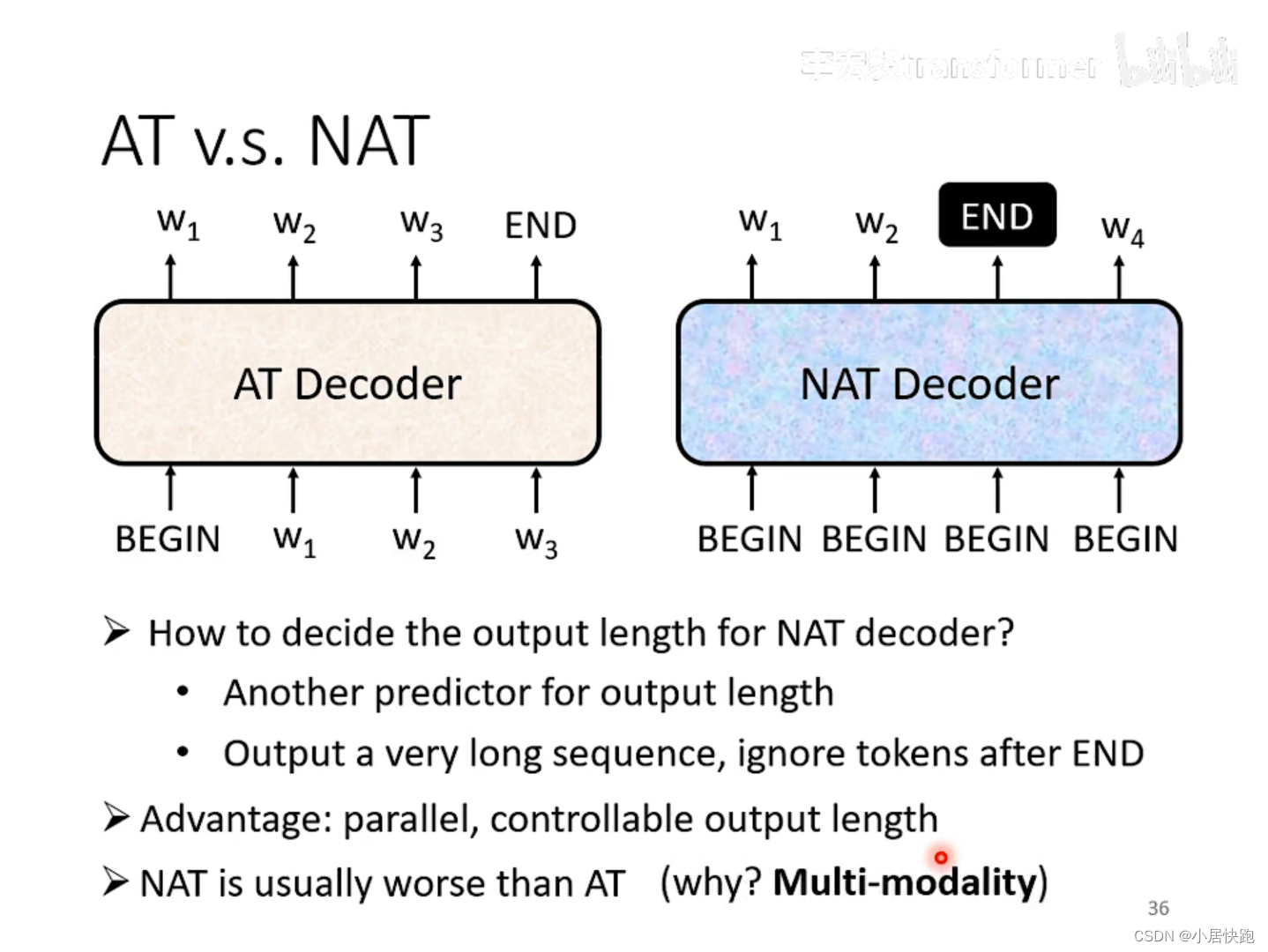
Non-autoregressive（NAT）

常用于語音合成領域，因為可以：輸出長度 * 2 -> 語速 * 2