---

---

[藍橋杯 2018 國 B] 調手表

題目描述

小明買了塊高端大氣上檔次的電子手表，他正準備調時間呢。

在 M78 星云，時間的計量單位和地球上不同，M78 星云的一個小時有 $n$ 分鐘。

大家都知道，手表只有一個按鈕可以把當前的數加一。在調分鐘的時候，如果當前顯示的數是 $0$，那么按一下按鈕就會變成 $1$，再按一次變成 $2$。如果當前的數是 $n?1$，按一次后會變成 $0$。

作為強迫癥患者，小明一定要把手表的時間調對。如果手表上的時間比當前時間多 $1$，則要按 $n?1$ 次加一按鈕才能調回正確時間。

小明想，如果手表可以再添加一個按鈕，表示把當前的數加 $k$ 該多好啊……

他想知道，如果有了這個 $+k$ 按鈕，按照最優策略按鍵，從任意一個分鐘數調到另外任意一個分鐘數最多要按多少次。

注意，按 $+k$ 按鈕時，如果加 $k$ 后數字超過 $n?1,$ 則會對 $n$ 取模。

比如，$n=10,k=6$ 的時候，假設當前時間是 $0$，連按 $2$ 次 $+k$ 按鈕，則調為 $2$。

輸入格式

一行兩個整數 $n,k$，意義如題。

輸出格式

一行一個整數。表示：按照最優策略按鍵，從一個時間調到另一個時間最多要按多少次。

樣例 #1

樣例輸入 #1

5 3

樣例輸出 #1

2

提示

【樣例解釋】

如果時間正確則按 $0$ 次。否則要按的次數和操作系列之間的關系如下：

1. +1
2. +1, +1
3. +3
4. +3, +1

【數據約定】

對于 $30\%$ 的數據 $0<k<n\le 5$。

對于 $60\%$ 的數據 $0<k<n\le 100$。

對于 $100\%$ 的數據 $0<k<n\le 10^5$。

時限 3 秒, 256M。藍橋杯 2018 年第九屆國賽

---

---

題意解析

• 對于手表的某一時刻，調到另一時刻最少需要按多少次，然后取最大次數。
  • 需要注意的是，我們有倆按鍵：+1和+k
  • 拿 $n=10,k=6$ 舉例：
    
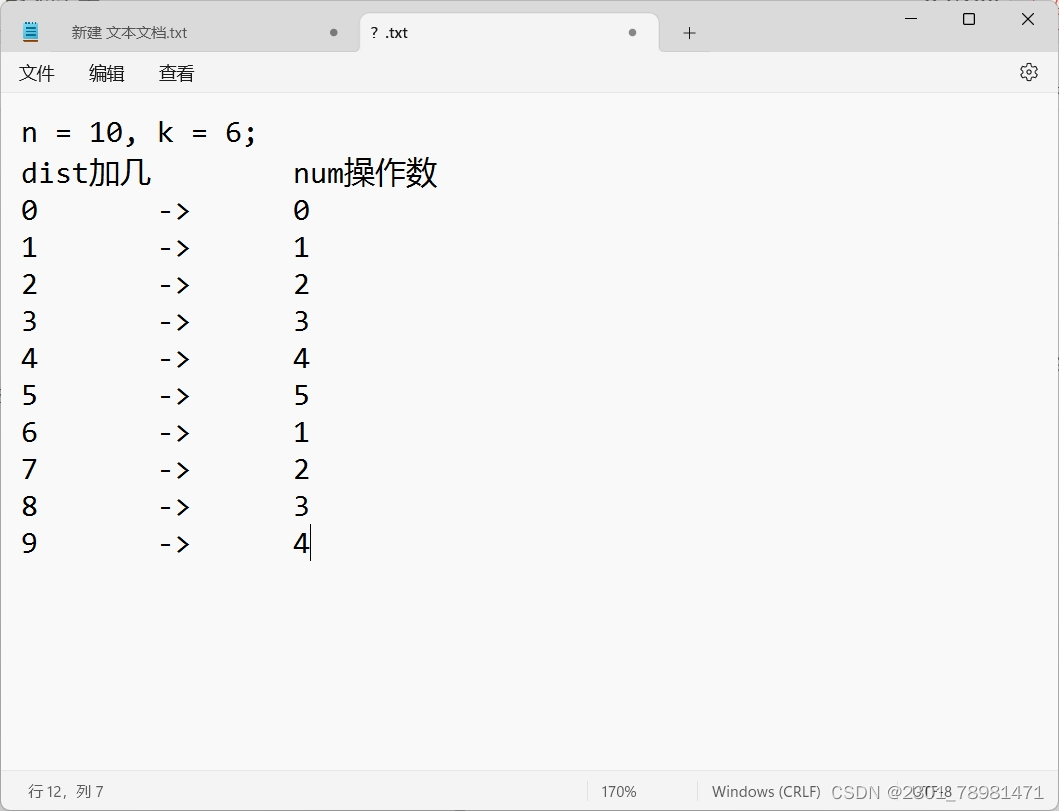
    • 我們先從+0開始，這一步需要 $0$ 次操作。
    • 從最少的操作，目前是 $0$ 開始往后延伸：分別+1和+6。
      • +1：那么就是 $0+1=1$，也就是說+1操作需要 $1$ 步。
      • +6：那么就是 $0+6=6$，也就是說+6操作需要 $1$ 步。
    • 以此類推，每次都要以最小的那個操作數為源點往后延伸。

---

CODE

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#define ll long long
#define INF 0x3f3f3f3f using namespace std;typedef pair<int, int> pii;  // 定義一個類型，表示一對整數const int N = 1E5 + 10, M = 2E5 + 10;
int n, k;  // n是點的數量，k是每次可以增加的步數
int h[N], e[M], ne[M], w[M],idx;  // h, e, ne用于存儲圖的信息，idx是當前邊的編號
int dist[N];  // dist用于存儲每個點到起點的最短距離
bool st[N];  // st用于標記每個點是否已經被訪問過
priority_queue<pii, vector<pii>, greater<pii>> heap;  // 定義一個小頂堆，用于存儲待處理的點
int maxnum = 0;  // 用于存儲最大的距離void add(int ver, int x){int des = (ver + x) % n;  // 計算下一個點的編號// 如果通過這條邊可以使得起點到終點的距離更短，就更新距離if(dist[des] > dist[ver] + 1){dist[des] = dist[ver] + 1;heap.push({dist[des], des});  // 將終點加入堆中}
}int dijkstra(){memset(dist, INF, sizeof dist);  // 初始化所有點到起點的距離為無窮大dist[0] = 0;  // 起點到自己的距離為0heap.push({0, 0});  // 將起點加入堆中while(heap.size()){auto t = heap.top();  // 取出堆頂元素heap.pop();int ver = t.second, dis = t.first;  // ver是點的編號，dis是起點到該點的距離if(st[ver]) continue;  // 如果該點已經被訪問過，就跳過st[ver] = true;  // 標記該點已經被訪問過maxnum = max(maxnum, dis);  // 更新最大的距離add(ver, 1), add(ver, k);  // 嘗試向前走一步和向前走k步}return maxnum;  // 返回最大的距離
}int main()
{cin >> n >> k;  // 輸入點的數量和每次可以增加的步數cout << dijkstra() << endl;  // 輸出最大的距離
}

---

分析一下復雜度

本題沒有m即邊數，而每次操作執行兩個情況，所以說邊數 $m=2$ 是個常量，那么除了樸素 $Dijkstra(O(n^2))$ 其他單源最短路應該都可以做。