【FMCW毫米波雷達設計】

原書：FMCW Radar Design

1? 引言

????????本章研究驅動FMCW雷達的主要波形:線性調頻(LFM)波形。我們研究信號的行為及其性質。隨后，本章討論了匹配濾波理論，并研究了壓縮這種波形的技術，特別是所謂的拉伸處理，它賦予FMCW雷達極高的壓縮比。最后，本章詳細介紹了FMCW技術背后的數學原理，包括距離分辨率問題、帶寬問題和整體性能問題，包括LFM波形的非線性及其影響。

2? FMCW?調頻連續波

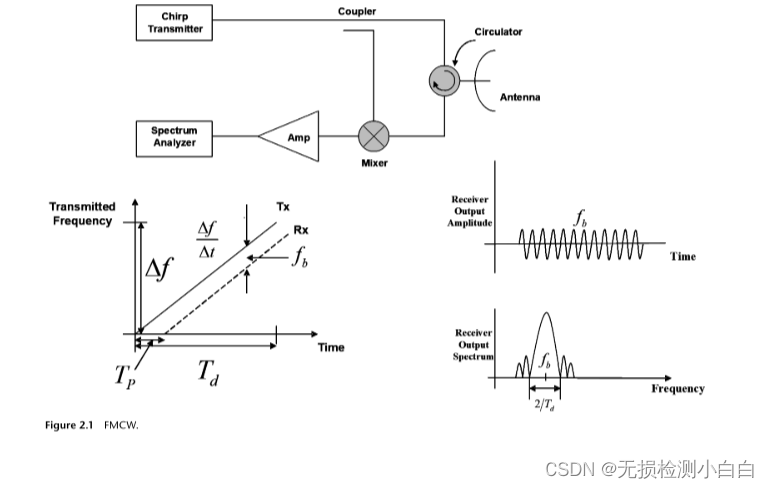
???????FMCW雷達與脈沖雷達的區別在于電磁信號是連續傳輸的[1,2]。這個信號的頻率隨著時間的變化而變化，通常是掃過一個設定的帶寬。發射和接收(反射)信號之間的頻率差是通過混合這兩個信號來確定的，從而產生一個新的信號，可以通過測量來確定距離或速度。鋸齒函數是最簡單的，也是最常用的，用來改變發射信號的頻率模式。FMCW雷達與傳統脈沖雷達系統的不同之處在于射頻信號是連續輸出的。因此，不能直接測量到反射物體的飛行時間。相反，FMCW雷達發出的射頻信號通常是線性掃頻的。然后接收到的信號與發射的信號混合，由于反射信號的飛行時間造成的延遲，會有一個頻率差，可以作為低頻范圍的信號檢測到。圖2.1是一種基于循環器的通用天線系統的示意圖。然而，通常有兩個完全獨立的天線，一個用于傳輸，一個用于接收。在這種情況下，問題是要確保天線之間足夠的隔離。問題是:為什么我們需要鋸齒函數，或者任何頻率調制?沒有調頻的簡單連續波雷達設備的缺點是，它們無法確定目標距離，因為它們缺乏必要的計時標記，使系統能夠精確計時，測量發射和接收周期，并將其轉換為距離。可以產生這樣一個時間基準來測量靜止物體的距離使用頻率調制的發射信號。在這種方法中，一個信號在頻率上周期性地增加或減少。當接收到回波信號時，頻率的改變會得到延遲Δt就像脈沖雷達一樣。然而，在脈沖雷達中，運行時必須直接測量。在FMCW雷達中，測量實際發射信號和接收信號之間的相位或頻率差異。

????????FMCW雷達的特點如下:

????????距離測量是通過將接收到的信號的頻率與參考信號(通常直接是發射信號)進行比較來完成的。

????????發射信號的持續時間大大大于所安裝的距離測量范圍所需的接收時間。

????????FMCW雷達的基本特點如下:

????????能夠測量非常小的范圍到目標;

????????能夠同時測量目標距離及其相對速度;

????????量程測量精度極高;

????????低頻范圍混合后的信號處理性能，大大簡化了處理電路的實現;

????????安全無脈沖輻射，峰值功率高。

????????我們現在更詳細地研究FMCW波形，作為其他技術的背景。

3? 線性調頻波形

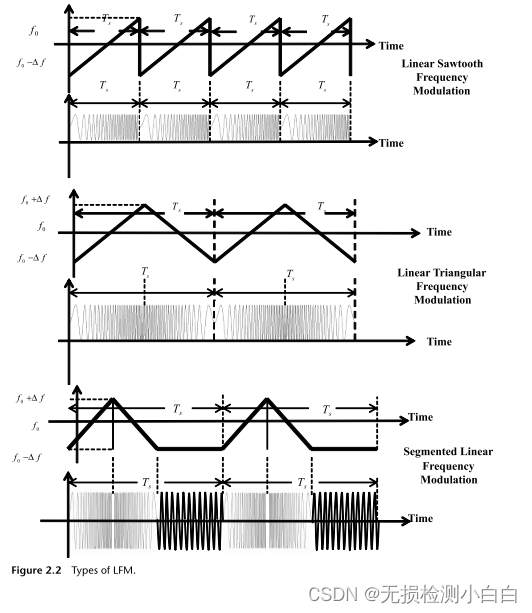
????????在我們對高分辨率的追求中，我們被驅使著去追求更高帶寬的信號。LFM就是這樣一個信號[1?3]。這是非常受歡迎的，而且有充分的理由，我們將會看到。基本上有三種LFM波形，它們在隱形雷達中非常流行:

????????1. 線性鋸齒波調頻;

????????2. 線性三角調頻;

????????3. 分段線性調頻。

????????這些調制形式如圖2.2所示。

4??線性鋸齒FMCW

????????這類信號的連續波形以鋸齒狀的方式傳輸，如圖2.2頂部所示。它的方程由，

???????????

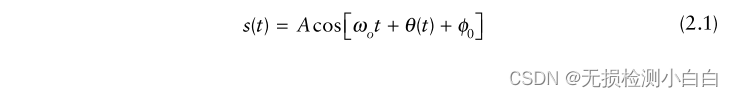
?????????這個信號的頻率由，

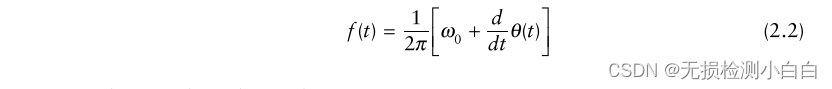
?????????其中θ(t)斜率為線性。

????????接收到的信號為:

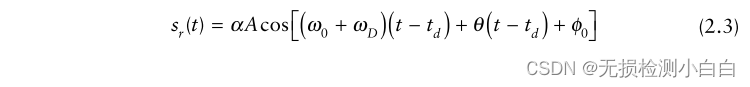
? ? ? ? 其中

? ? ? ? ? ? ? ? ? ? ? ?α是衰減因子

????????????????????????td = 2R/c為到目標的雙向時延

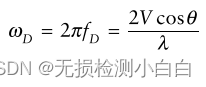? ? ? ? ? ? ???是多普勒頻移，Vcosθ是徑向速度，λ是波長

? ? ? ? ? ? ? ??接收信號的頻率由

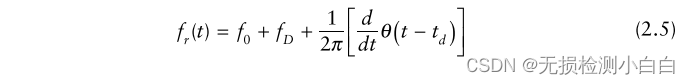
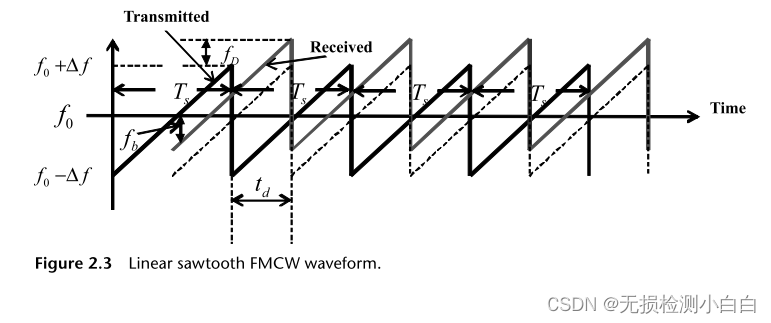
????????顯然，從圖2.3中可以明顯看出，發射波形和接收波形之間的差值構成了理想的純正弦波，稱為拍信號fb。這個拍頻信號正比于發射波形和接收波形之間的延遲，換句話說，就是目標距離。此外，接收的波形相對于發射波形向上移動(對于后退的目標)(見圖2.3)。這是由于目標多普勒，其值fD為(2.4)所定義的目標多普勒。鋸齒波形的周期稱為掃描時間，Ts。注意td是到目標的雙向時間延遲，沿x軸測量，而在頻率或y軸上的對應信號是fb，拍信號。

????????我們現在需要提取拍信號，fb。顯然，這可以通過減去發射和接收的波形來實現。這是通過混合(乘)這兩個信號和過濾下邊帶保留頻率的差異來實現的。從數學上(見圖2.4)，如下所示:拍信號的頻率為，

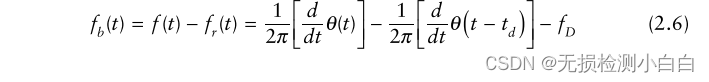
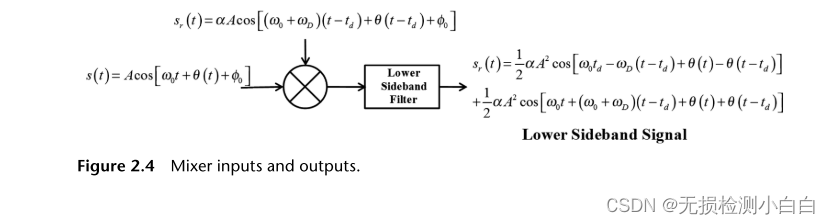?????????因此，返回信號的頻率與發射信號的頻率發生了變化，原因如下:

?????????????????雙向時延 td = 2R/ c;

?????????????????多普勒頻移? $f_{d} = 2V\cos \theta /\lambda$

????????

????????我們從圖2.5中注意到，

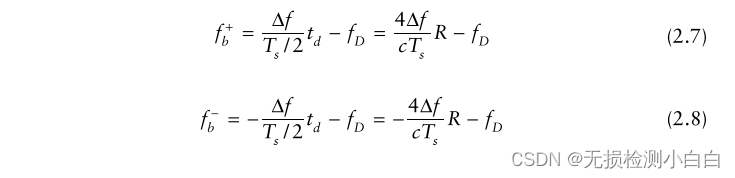
?????????因此，我們有兩個方程，兩個未知數，R和fD，其解，

?????????通過FFT得到fb +和fb?。利用這些和(2.9)(2.10)計算R和fD。然而，圖2.5中有一些有趣的地方。如果目標接近雷達，我們就會遇到向上多普勒情況。相反，如果目標遠離雷達，我們就會遇到下多普勒情況。例如，在上多普勒情況下，接收到的波形沿y軸(頻率軸)向下移動，如圖2.5所示。這是因為基本拍信號增加了目標的多普勒。如圖2.5所示，這意味著在沒有目標多普勒(靜態目標)的情況下，拍頻信號相對于標稱值的頻率會增加。相反，在下降多普勒期間，接收到的波形將沿著頻率軸向上傳播，降低拍信號的頻率。因此，總結起來，上多普勒增加了節拍信號的真實標稱值(這取決于目標的距離)，而下多普勒降低了節拍的頻率信號不要忘記拍信號的頻率是由圖2.5中發射和接收波形之間的間隙給出的。讀者可以更容易地通過查看圖2.5的頂部圖來理解這個問題，圖中包含了發送和接收波形。然而，我們知道拍信號的頻率與目標距離直接相關。(我們稍后將在第2節中討論這些方程。)但真實目標距離受到目標多普勒的影響，因為由于目標多普勒的作用，拍頻信號的頻率從其真實值變為目標靜態。這種現象稱為距離-多普勒耦合，其中由于目標多普勒而產生距離誤差。第三章探討了這些問題。在圖2.5中，多普勒濾波器在上多普勒(或拍信號增大)時出現4個峰值，而在下多普勒情況下，濾波器1出現峰值，因為拍信號頻率減小。因此，我們可以直接讀取fb +和fb?，然后計算距離和多普勒。請注意，在圖2.5中，如果沒有目標多普勒(即目標是靜態的)，那么拍信號波形將是圍繞x軸對稱的 $f_{b}^{+} = -f_{b}^{-}$ 。

4.1? 線性調頻波形

?????????現在我們考慮鋸齒波形本身。我們基本上有兩大類線性調頻信號定義的線性掃描特性，上行啁啾或下行啁啾。匹配的濾波器帶寬與掃描帶寬成正比，與脈沖寬度無關。圖2.6顯示了兩種LFM信號。

?????????線性調頻上行啁啾瞬時相位表示為

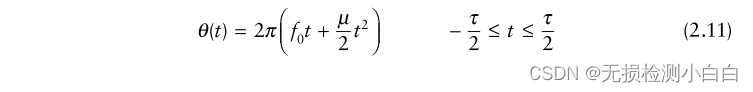
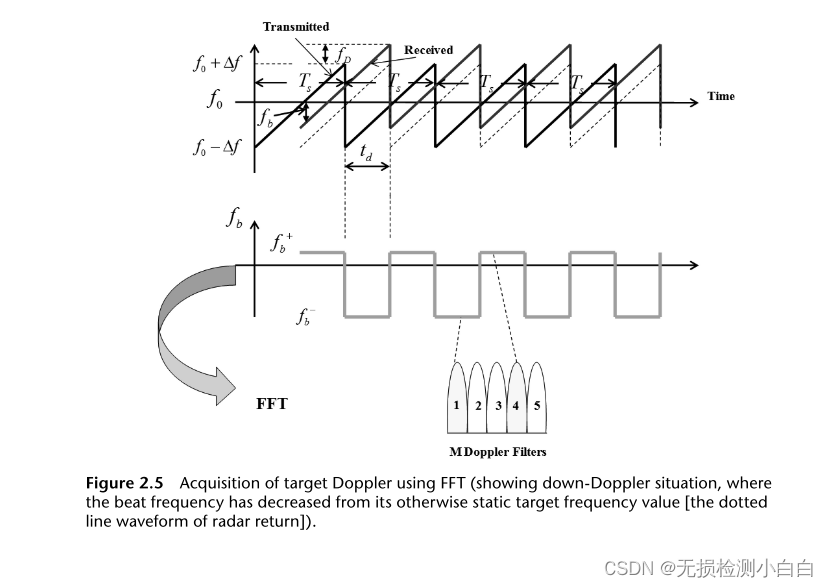
???????圖2.5 FFT捕獲目標多普勒(下圖為下多普勒情況，拍頻從靜止的目標頻率值[雷達回波虛線波形]開始下降)。

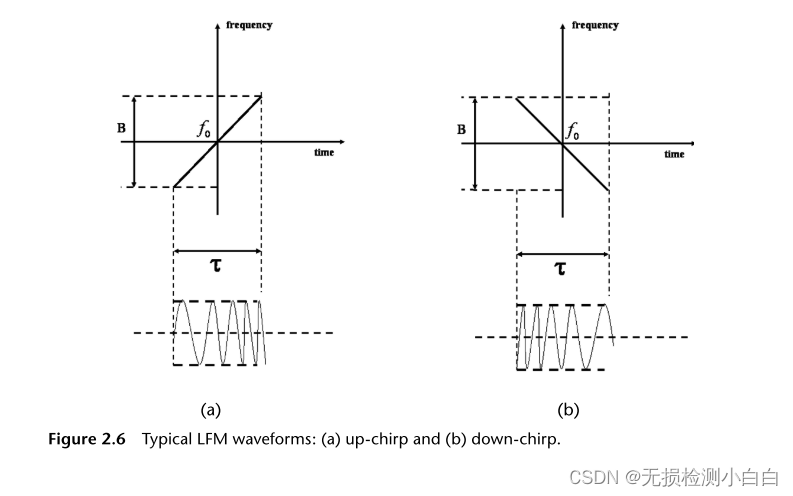
????????式中，f0為雷達中心頻率，μ = (2πB)/τ為LFM系數。因此瞬時頻率為

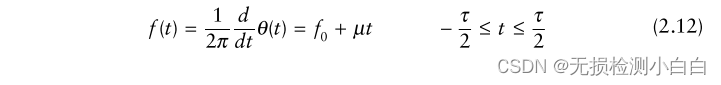
????????類似地，對于下啁啾，

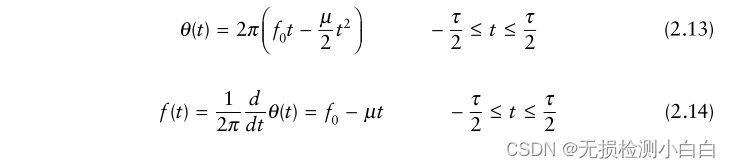
????????一個典型的LFM波形在時域[1]中有如下表達式:

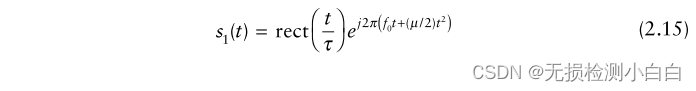
????????????????其中

???????????????????????? $rect(t/\tau )$ 表示寬度為τ的矩形脈沖。

????????????????????????(2.15)可以改寫為

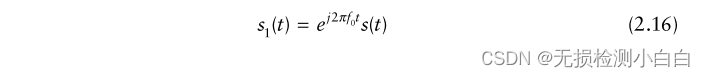
?????????????????其中

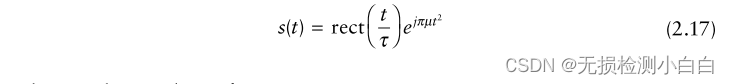
????????????????是s1(t)的復包絡線。

????????在頻域，(2.17)的FT經過一些操作后得到[1]

? ? ??

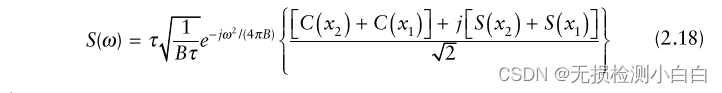
? ? ? ? ? ? ? ? 其中

? ? ? ? ? ? ??

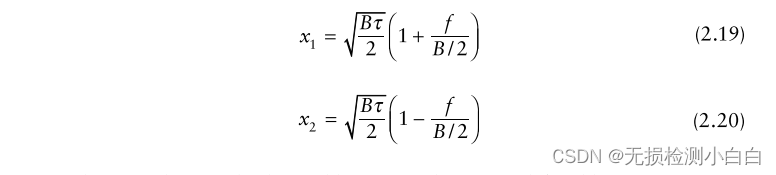
????????????????菲涅耳積分，用C(x)和S(x)表示，定義為

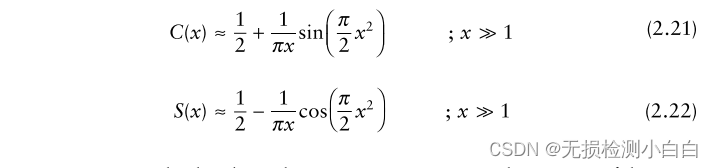
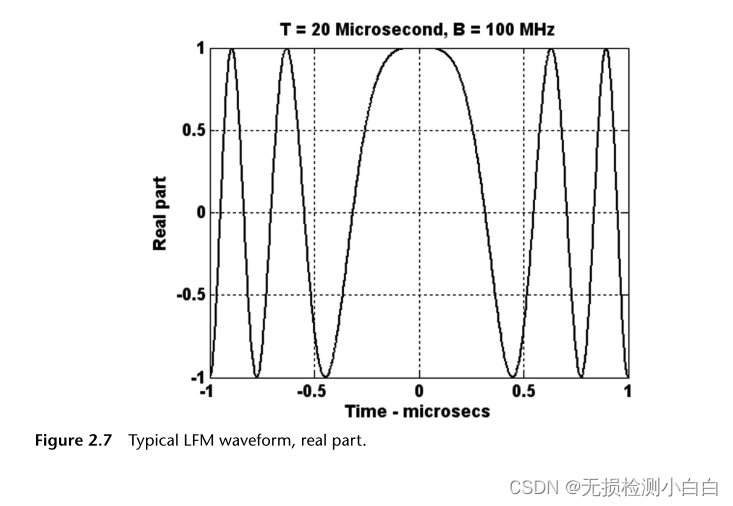
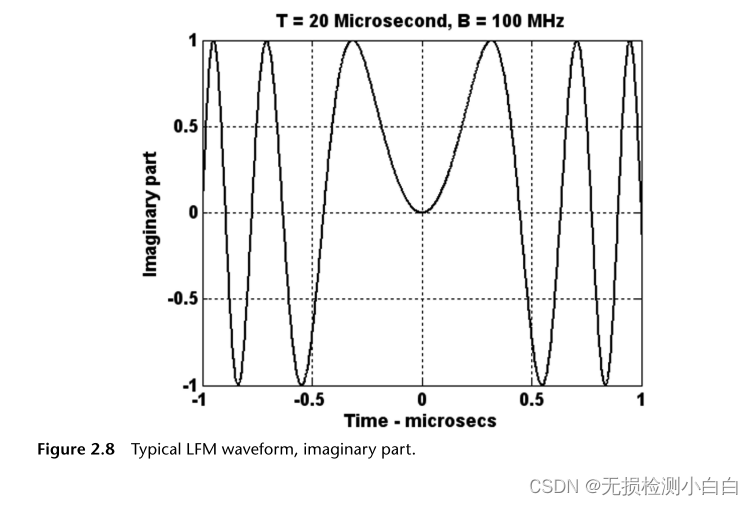
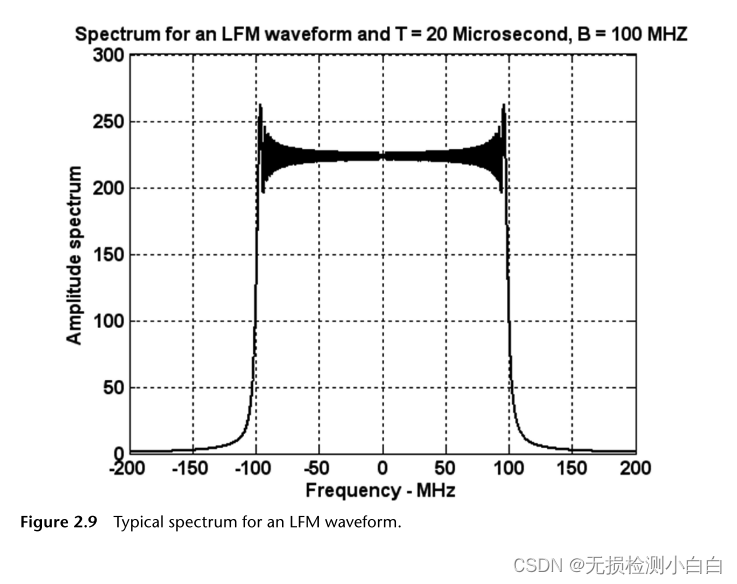
????????圖2.7 ~ 2.9顯示了LFM信號的實部、虛部和頻譜。LFM帶寬為100 MHz，未壓縮脈沖寬度為20 μs。

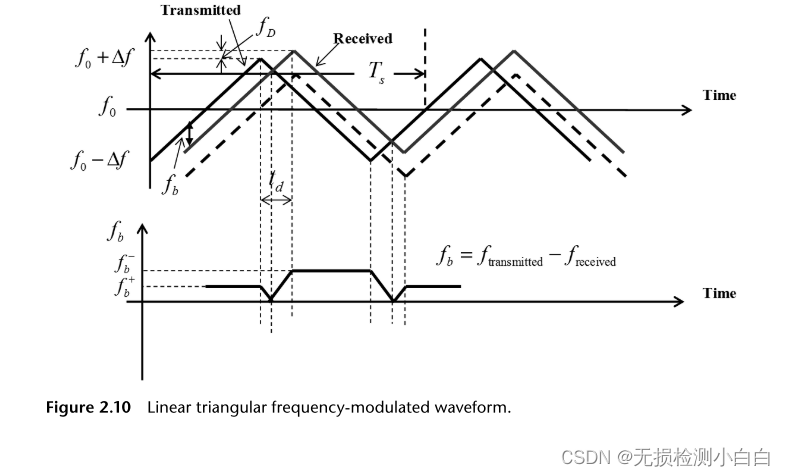
5? 線性三角形FMCW

?????????信號處理的初始階段與鋸齒波形的初始階段相同。與鋸齒波形(見圖2.10)一樣，接收到的拍信號由(2.6)給出，重現如下:

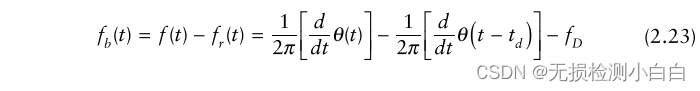
????????同樣，目標的距離和多普勒由(2.9)和(2.10)定義。然而，相似之處就到此為止了。當評估多個目標時，三角波形會產生問題。我們將從一個目標開始，就像處理鋸齒波形一樣。

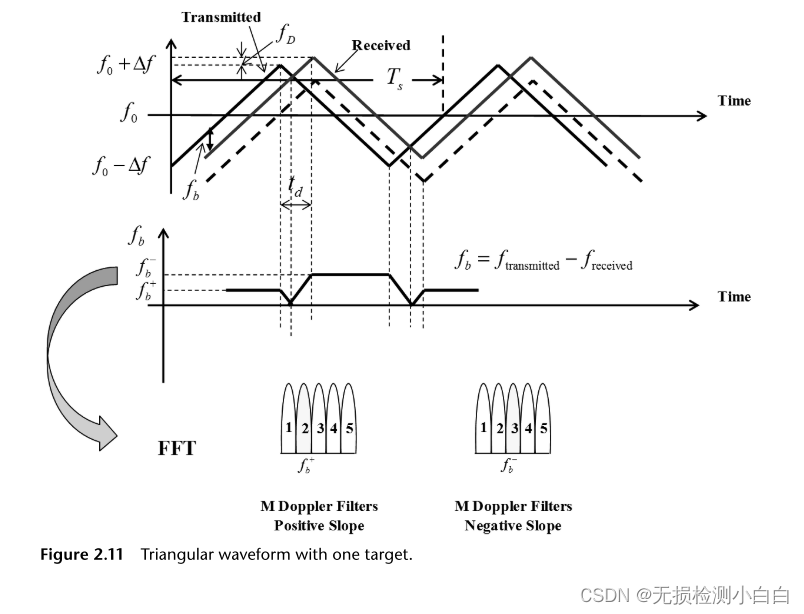
5.1? 單個目標

????????當我們對正斜率進行FFT時，我們得到 $f_{b}^{+}$ ，而在負斜率上，我們得到 $f_{b}^{-}$ 。如圖2.11所示。在這種情況下，R和fD由(2.9)和(2.10)定義。然而，如果有兩個目標，那就完全是另一回事了。

5.2? 兩個目標

????????在這種情況下，如圖2.12所示，當我們對每個正斜率和負斜率進行FFT時，我們在每個多普勒窗口得到兩個節拍，我們不能將哪個節拍與哪個目標相關聯。我們通過添加一個未調制的線段[1]來解決這個問題。

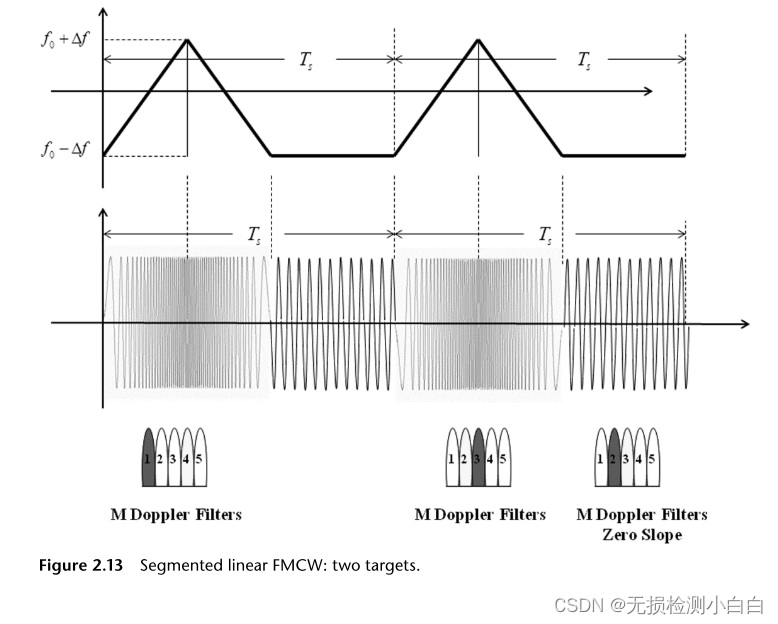
6? 分段線性FMCW

????????在圖2.13中，正斜率產生了兩個回波。同樣，負斜率也產生了另外兩個回聲。然而，為了解決歧義，我們使用一個零斜率的未調制截面。這能得到每個目標的準確多普勒信號。知道多普勒值后，我們將 $f_{b}^{+}$ 和 $f_{b}^{-}$ 代入(2.10)，直到滿足該方程。這意味著這個聯想是正確的。現在我們可以使用(2.9)來計算距離。另一種解決距離和多普勒模糊的方法是使用許多調制斜率(Δf 和 $T_{s}$ )。?

????????我們現在計算FMCW雷達的兩個主要參數:掃頻帶寬和到目標的距離。

7? 掃描帶寬的推導

????????載波頻率隨時間線性增加[1?5]。坡道坡度由Δf/Δt給出。在往返時間Tr = 2R/c后接收到回波，其中R為到目標的距離。

????????回波與部分發射信號混合(零拍混合)以產生輸出拍頻fb。

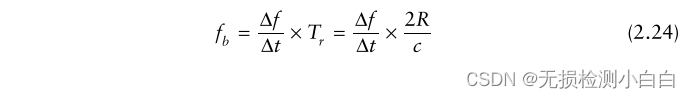
?????????從圖2.1可以看出，輸出將是一個恒定的頻率，除了在周轉時間的掃描的極端。

?????????如果所需的距離分辨率為ΔR，則所需的頻率分辨率為 $\Delta f_{b}$

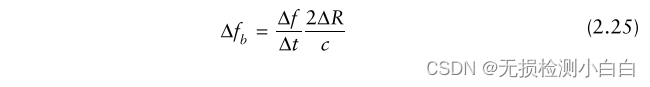
?????????對于 $\Delta f_{b}$ 的光譜分辨率，信號必須觀測到Td = 1/ $\Delta f_{b}$ 的最小駐留時間

? ??

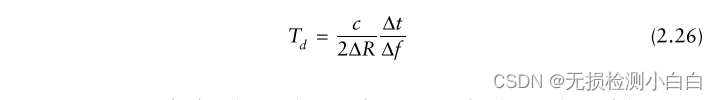
?????????在斜坡速度為Δf/Δt時，總掃頻 Δf 是掃頻和停留時間的乘積:

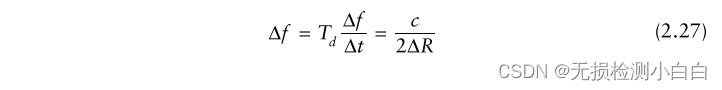
?????????式(2.27)表示所需距離分辨率越高，所需信號帶寬越大。這個推論與脈沖雷達的推論是一樣的。

8? 計算距離

????????一般來說，使用下面的關系從測量到的拍頻計算出距離

? ? ? ?

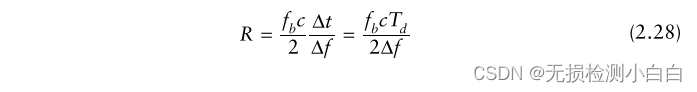
????????注意，Td是傳播到目標的時間(范圍)，也是所需光譜分辨率的最小駐留時間[見(2.26)]。掃描時間Ts是FMCW波形的總掃描時間，比Td大得多。原因將在2.16節稍后討論。

9? 匹配過濾器

????????匹配濾波器[1?4]是這樣一個濾波器，其脈沖響應由這樣一個特殊的信號決定，當信號和白噪聲都經過濾波器時，濾波器輸出的信噪比可達到最大。這種濾波器廣泛應用于雷達。

????????考慮一個帶有加性高斯白噪聲的雙側信號s(t)，其譜密度為N0/2，通過一個頻率傳遞函數H(ω)的線性濾波器。擺在我們面前的問題如下:

????????在給定的觀測時間tM下，輸出的信噪比最高的濾波器響應是什么?

????????因此，我們需要尋找這樣一個傳遞函數H(ω)來完成這項工作，并使所給的信噪比最大化

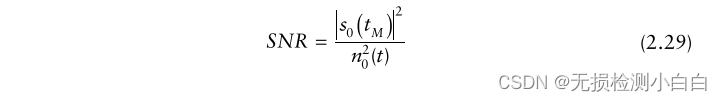
????????如果s(t)的傅里葉變換是s(ω)那么 tM 處的輸出信號由

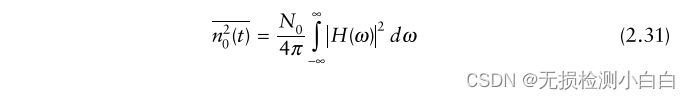
????????將(2.30)和式(2.31)代入(2.29)得到

????????我們現在使用Schwartz不等式，它說對于任意兩個復信號A(ω)和B(ω)，下面的不等式是成立的

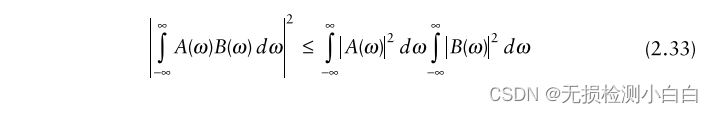
????????這個等式成立

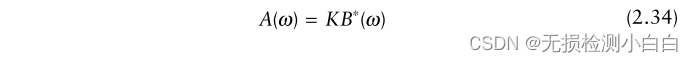
????????其中 * 為復共軛，K為任意常數。

????????將Schwartz不等式應用于(2.32)，我們得到

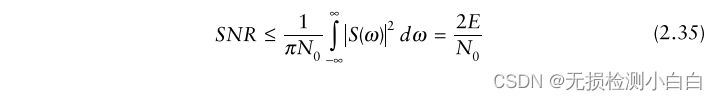
????????E是信號的能量。此時為相等，即最大信噪比

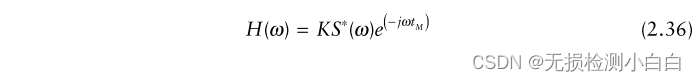????????由式(2.35)可知，2E/N0是可達到的最高峰值信噪比。H(ω)的傅里葉反變換將產生所需濾波器的脈沖響應

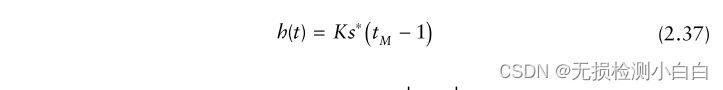
????????檢查(2.37)可知H(ω) = K?S(ω)?，這意味著濾波器根據信號的頻譜來衡量其頻率響應。脈沖響應表明它是信號共軛的延遲鏡像。對于因果濾波器，當t < 0時，h(t)必須為零。這只有在tM等于或大于信號的持續時間s(t)時才會發生。

????????如果我們將輸入信號與與之匹配的濾波器的脈沖響應卷積，我們得到

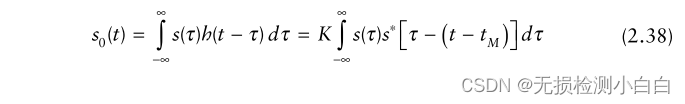
????????如果讓 t = tM ，就得到

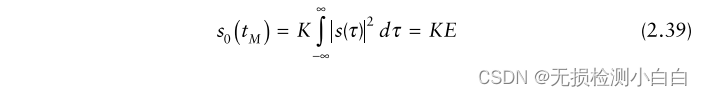
????????即在tM處，輸出信號與輸入信號的能量成正比。這適用于所有通過其匹配濾波器的信號。

????????因此，綜上所述[4,5]，在白噪聲存在的情況下，匹配濾波器的輸出信噪比是可達到的最高的:2E/N0。這個輸出信噪比是信號能量E的函數，但不是信號的形式。當噪聲是非白噪聲時，或者當分辨率、精度和檢測等其他因素很重要時，信號的形式就很重要了。

????????例子

????????當脈沖響應匹配到信號 $s(t) = exp(-t^2 / 2T)$ s(t) = exp(?t2/2T)時，線性濾波器輸出的最大瞬時信噪比是多少?

????????答案

????????信號能量為

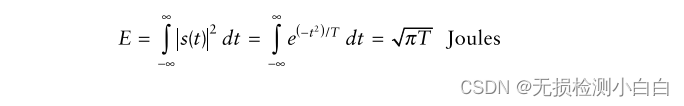
????????因此，最大瞬時信噪比為

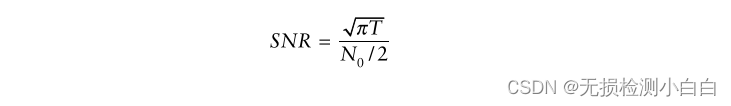
?????????式中，N0/2為輸入噪聲功率譜密度。

10? 存儲副本

????????匹配濾波器輸出可以從雷達接收信號和發射波形的延遲副本之間的互相關計算出來。在數學上和結構上，這與(2.37)中給出的表達式所定義的是一樣的。如果輸入信號與發射信號相同，則匹配濾波器的輸出為接收(或發射)信號的自相關函數。這是一種非常流行的實現這種濾波器的方法，在實踐中，傳輸波形的副本通常被計算并存儲在內存中，以供雷達信號處理器在需要時使用。

11? 時間-帶寬乘積

????????我們現在檢查一個匹配的濾波雷達接收機。濾波器具有前面討論過的雙側頻譜的白噪聲帶寬。這個噪聲功率由

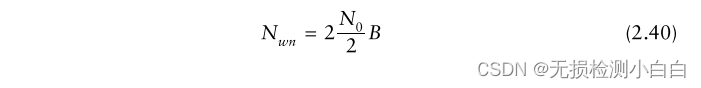
????????其中B是匹配的濾波器帶寬，用2的因子來考慮負頻段和正頻段，如圖2.14所示。

????????在信號持續時間T內的平均輸入信號功率為[2]

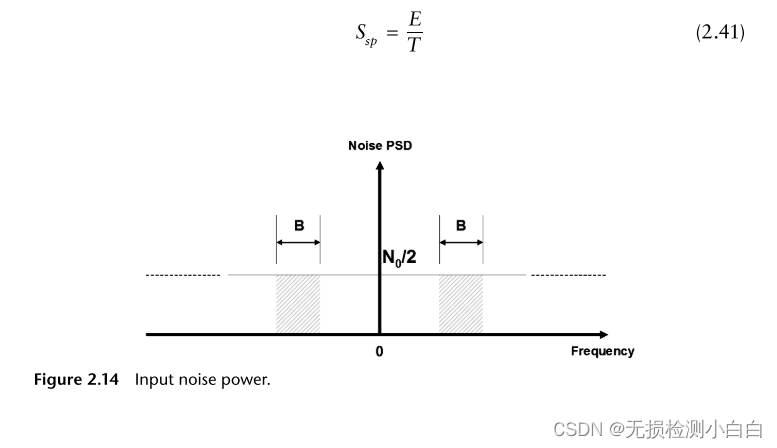
?????????其中E為信號能量。因此，匹配的濾波器輸入信噪比為

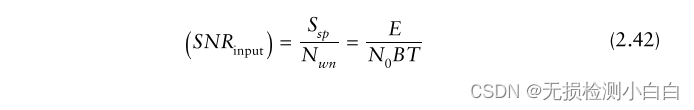
????????輸出峰值瞬時信噪比與輸入信噪比為

????????數量BT被稱為給定波形或其相應匹配濾波器的時間-帶寬乘積。輸出信噪比比輸入信噪比增加的因數BT稱為匹配濾波器增益，或壓縮增益。

????????未調制信號的時間帶寬乘積接近統一。我們可以通過使用頻率或相位調制，使信號的時間和帶寬乘積大于一個單位。如果雷達接收匹配濾波器與輸入波形完全匹配，壓縮增益等于BT，如果匹配濾波器頻譜偏離輸入信號的頻譜，壓縮增益成比例下降。

12? 波形壓縮

????????為了在雷達中獲得高分辨率，必須增加信號帶寬。這在非調制脈沖雷達中是通過發射非常短的脈沖來實現的。然而，如果我們使用短脈沖，我們也降低了平均發射功率，因此，雷達探測距離。因此，我們需要尋找一種方法，使我們能夠以較大的平均功率(通過使用長脈沖)發射，同時實現與短脈沖相同的距離分辨率。隨著線性調頻脈沖的出現，這種異常情況得到了解決。LFM脈沖利用寬帶寬和大平均功率發射一個長脈沖，然后使用下面討論的脈沖壓縮技術對接收的脈沖進行壓縮，以達到預期的距離分辨率。因此，脈沖壓縮可以讓我們獲得長脈沖的平均發射功率，同時獲得短脈沖對應的距離分辨率。在連續波雷達中，我們用波形壓縮來代替脈沖壓縮。從此以后，我們將在本書中使用這個術語。

????????有兩種著名的技術來實現波形壓縮:

????????????????相關處理;

????????????????拉伸加工。

12.1? 線性調頻波形壓縮

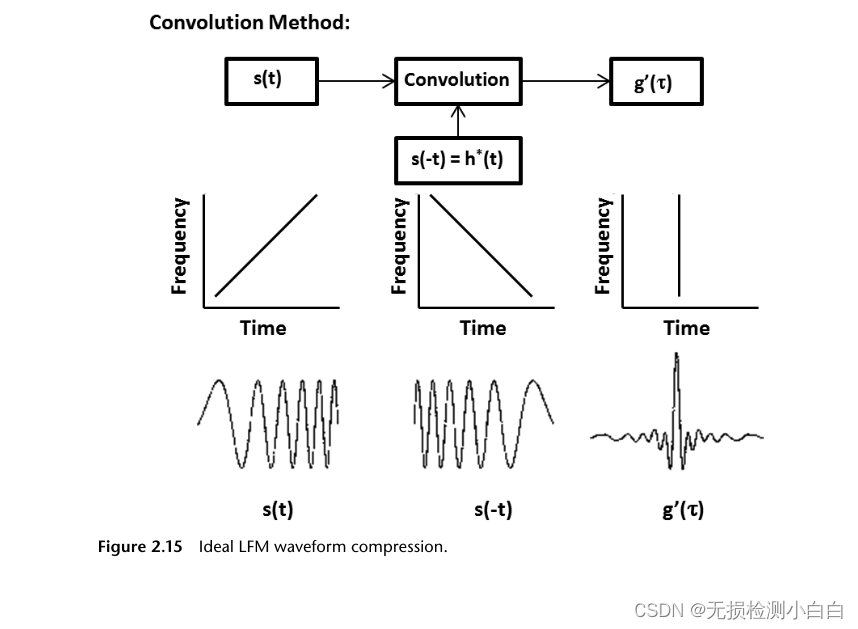
????????LFM波形壓縮是通過在傳輸時對長啁啾信號進行調頻和使用匹配的濾波器接收機來壓縮接收到的信號來實現的。因此，匹配的濾波器輸出被一個因子BT壓縮，其中T是未壓縮的信號寬度，B是LFM信號的帶寬。因此，我們可以使用長啁啾信號和LFM調制來實現大的壓縮比。圖2.15顯示了LFM波形壓縮過程。

????????圖2.15顯示了與匹配濾波器進行卷積的LFM波形。匹配的濾波器輸入/輸出波形也顯示出來。與頻率域的輸入波形相比，輸出在時域是一個壓縮脈沖。請注意，匹配濾波器的波形是輸入信號的鏡像逆。

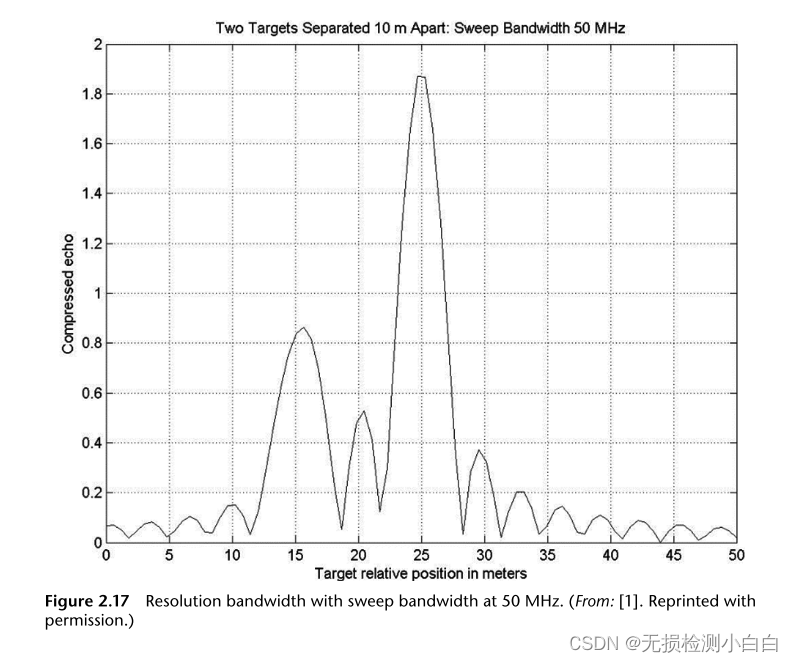
????????我們現在檢查波形壓縮帶寬的影響。我們假設在15m和25m處有兩個RCS 1 m2和2 m2的目標。在初始情況下，掃描帶寬為10 MHz。接收窗口為50m。掃描時間為10 μs。這種情況下的距離分辨率由

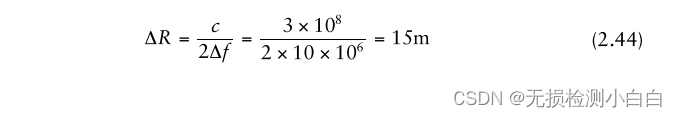
????????這也被稱為瑞利分辨率。由于帶寬不足，雷達無法分辨目標。如果我們現在把帶寬增加到50兆赫茲，那么

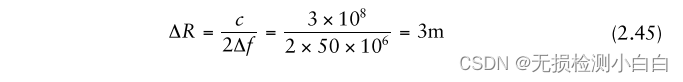
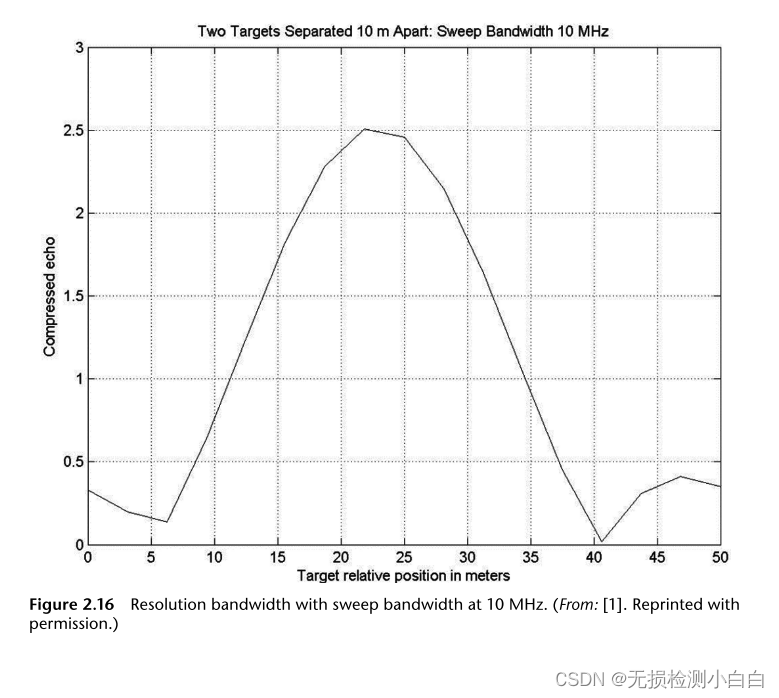
?????????很明顯，雷達現在可以分辨目標。該程序在附帶的軟件中給出，并命名為“LFM_resolve.m”。結果如圖2.16和2.17所示。

????????至此，我們已經看到了匹配濾波器是如何進行LFM波形壓縮的。但是這種匹配的過濾器是如何實現的呢?

12.2? 相關處理器

????????我們將雷達距離窗口定義為雷達最大和最小距離的差值。這也稱為接收窗口。收集接收窗口內的所有目標返回，并通過匹配的過濾器進行波形壓縮。這個匹配的過濾器可以通過多種方式實現。一是使用聲表面波(SAW)裝置[6]。另外，我們可以使用FFT進行數字相關處理。這種方法叫做快速卷積處理(FCP)。如圖2.18所示。為了使兩個長序列相關聯，必須進行傅里葉變換，然后將一個序列與另一個序列的復共軛乘積，最后進行傅里葉反變換完成這一過程。

????????將發射序列裝入參考寄存器，通過信號移位寄存器對輸入序列連續計時。在每個時鐘周期上，比較計數器形成匹配的總和，并減去移位寄存器的相應級之間的不匹配，以產生相關函數。這種方法也稱為FCP。????????

????????現在，我們參考FCP來研究這個過程背后的數學原理，如圖2.18所示。

????????定義的接收窗口

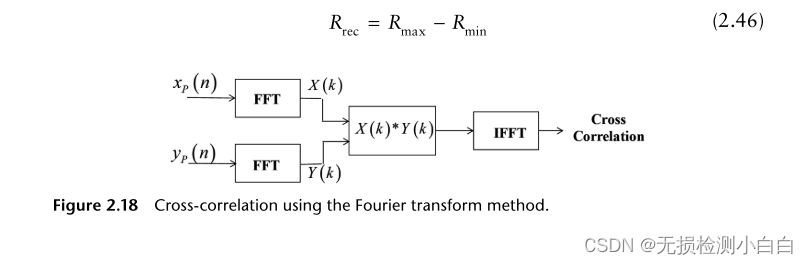
?????????其中Rmax和Rmin分別定義雷達探測距離的最大值和最小值。歸一化復發射信號的形式為[1]

?????????其中 T 為信號寬度，μ = B/T, B為帶寬。

????????雷達回波與發射信號相同，但有一個與目標RCS相對應的時間延遲和振幅變化。我們假設目標位于距離R1的位置。這時雷達接收到的回波

?????????其中a1與目標RCS、天線增益和距離衰減成正比。時間延遲 τ1 由

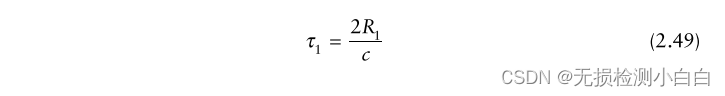
?????????最初，我們去除頻率fo。這是通過將接收信號srec(t)與相位為2πfot的參考信號混合來實現的。合成信號經過低通濾波后的相位由

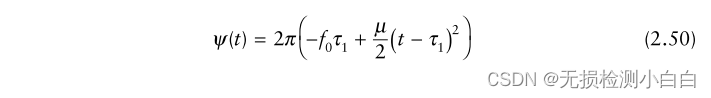
?????????瞬時頻率為

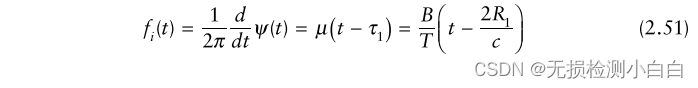
?????????正交分量是

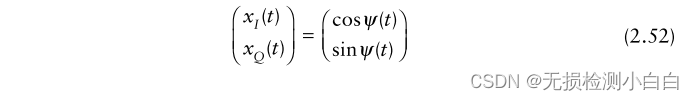
?????????接下來，我們通過選擇采樣頻率 fs >2b 對正交分量進行采樣(以滿足Nyquist準則，從而避免頻譜中的模糊性)。則采樣間隔為 Δt≤1/2B。由式(2.51)可知，FFT的頻率分辨率為

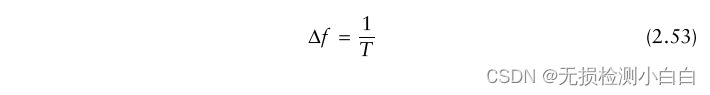
????????最低要求的采樣數量是

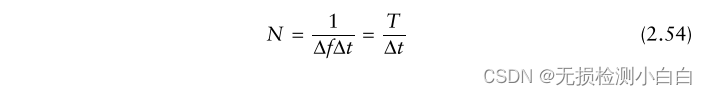
????????利用 Δt≤1/2B 代入(2.54)得到

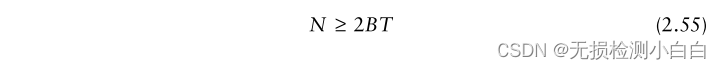
????????因此，我們需要總共 2BT 的實采樣或BT的復采樣來完整描述一個持續時間T和帶寬B的LFM波形。例如，一個持續時間T = 10 μsec，帶寬B = 4 MHz的LFM信號需要80個實采樣來確定輸入信號 (? i? 通道40個采樣，q? 通道40個采樣)。

????????假設接收窗口內有I個目標，范圍為R1、R2等，那么根據疊加定理，下轉換信號的相位為[7-9]

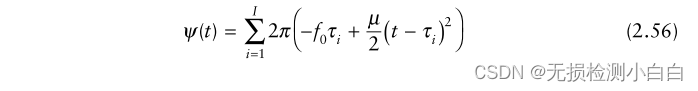
????????時間 {τi = (2Ri / c); i = 1,2，…，i} 為雙向時延，其中 τi 與接收窗口開始時間重合。該方法已在Simulink?中實現。它在隨附的程序中給出(參見FCP.mdl)。

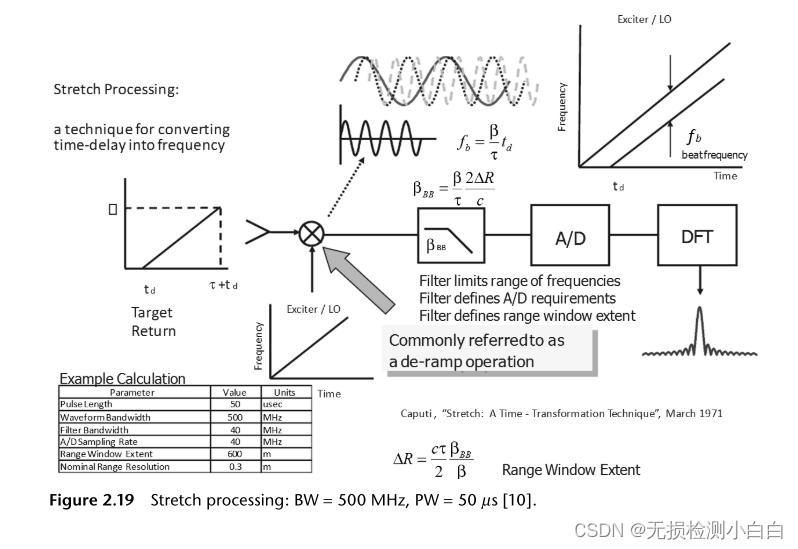
12.3拉伸處理器

????????伸縮處理，也稱為主動相關，是為了處理極寬帶寬的LFM波形。我們現在更詳細地研究這一重要技術，因為它在FMCW雷達中非常流行[1,5]。

????????我們現在用數學方法證明拉伸信號處理。這是基于[5,6]的推導。歸一化后的傳輸信號可以表示為

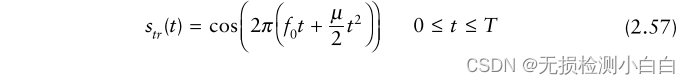
????????其中，μ = B/T為線性調頻系數，f0為調頻啟動頻率。假設距離R處有一個點散射體，雷達接收到的信號為

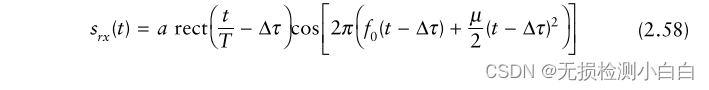
????????其中a與目標RCS、天線增益和距離衰減成正比。延遲時間為Δτ = 2R/c。參考信號為

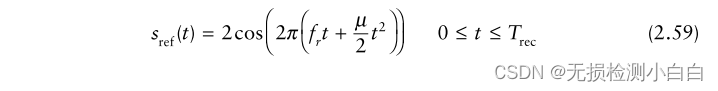
????????接收窗口為

?????????如果沒有傳播延遲(即Δt = 0)，則fr = f0，換句話說，fr和f0是相同的頻率，唯一的區別是前者屬于發射信號，后者屬于接收信號。因此，為了這個推導，我們可以聲明fr = f0。混頻器的輸出是接收到的信號和參考信號的乘積。經過低通濾波，

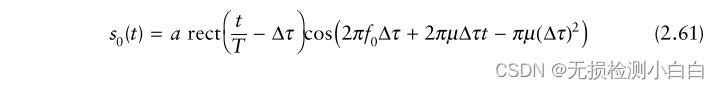
????????利用Δτ = 2R/c，代入(2.61)，得到

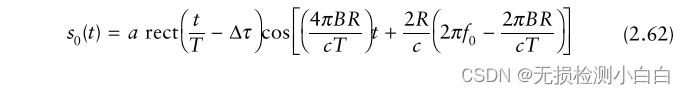
????????由于，T >> 2R/c，我們可以將(2.62)近似為

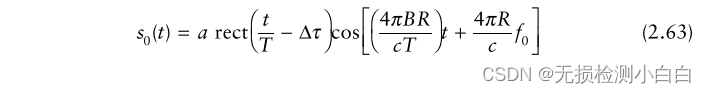
????????瞬時頻率為

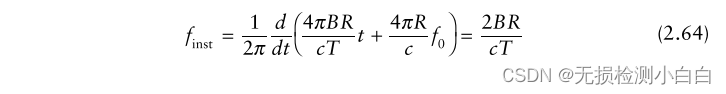
????????這清楚地表明了目標范圍與瞬時頻率成正比。因此，對LPF輸出進行采樣并進行FFT后，我們得到

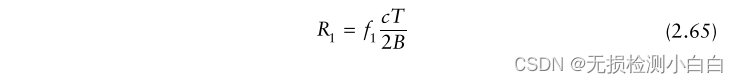
????????頻率為f1的R1的目標。

????????如果有 I 個距離為R1、R2等的近距離目標(R1 < R2 <…RI)，通過疊加得到，總信號為

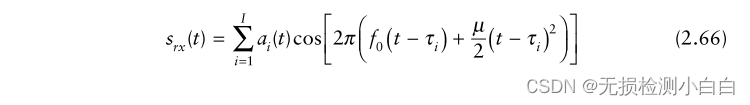
?????????其中 {ai(t);i = 1,2，…，i} 與目標的橫截面、天線增益、距離成正比。時間 {τi = (2Ri/c); i = 1,2，…，i} 為雙向時延，其中τi與接收窗口開始時間重合。使用(2.62)LPF輸出的整體信號可以描述為????????

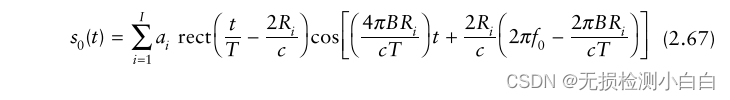
?????????因此，目標返回顯示為可以使用FFT分解的恒定頻率的音調。因此，確定適當的采樣率和FFT大小是關鍵。在[9]中證明了樣本個數N由

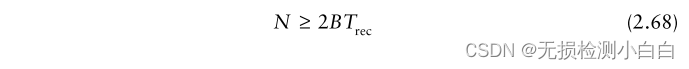
?????????如果我們用匹配濾波器來處理LFM脈沖，匹配濾波器的脈沖響應是，

?????????我們把rect(x)看成一個偶函數。

?????????由式(2.69)可知，匹配濾波器的帶寬要求為? $B = \mu \tau {_{T}}$ ?。這種寬帶信號處理器的成本很高。線性調頻匹配濾波器的常用方法是聲表面波壓縮器和數字信號處理器。聲表面波傳感器的有效頻率可達3ghz左右。如果我們使用數字信號處理器，我們會受到adc采樣速度的限制。這通常在3ghz左右。拉伸處理通過放棄整個雷達范圍的處理，而支持窄帶處理來解決這個難題。在匹配濾波器中，我們將在整個波形脈沖重復間隔(PRI)中尋找目標。另一方面，在拉伸處理中，我們被限制在一個通常小于未壓縮脈沖寬度的范圍內。因此，拉伸加工在求解距離較近的目標時得到了廣泛的應用。然而，必須記住，拉伸處理只能緩解匹配濾波器的帶寬要求，而不是整個雷達。例如，天線、發射機和接收機必須有較寬的帶寬來處理信號。圖2.19總結了拉伸處理中的問題[10,11]

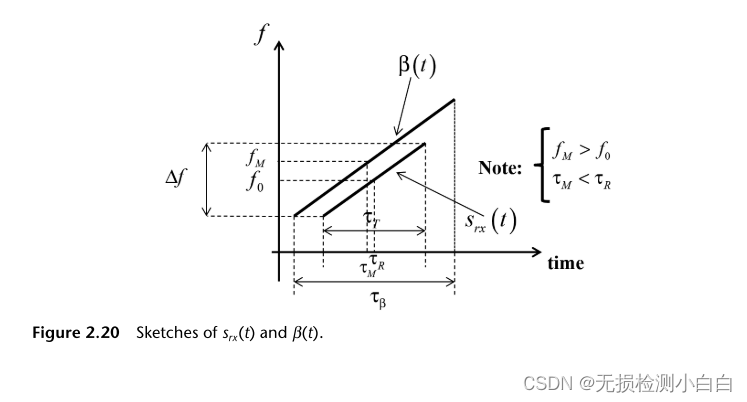
????????圖2.20給出了srx(t)和β(t)的概念草圖。兩者都是線性調頻信號。它們的頻率隨時間線性增加。然而，它們的持續時間是不同的。在信號持續時間方面，β(t)總是遠遠大于srx(t)。兩個信號的斜率都是μ。

????????圖2.20還告訴我們所需的 $\tau _{_{\beta }}$ 值，即外差信號的持續時間。對于所有τR的期望值，都需要保證srx(t)完全包含在β(t)內。這意味著，

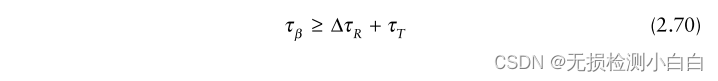
????????其中

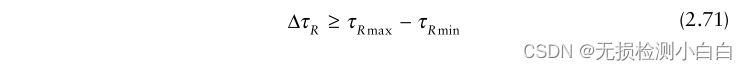
????????是我們想要執行拉伸處理的范圍延遲范圍。如果τβ滿足上述約束，則β(t)將完全重疊srx(t)，拉伸處理器將提供與匹配濾波器[5]幾乎相同的信噪比性能。否則，會有一定比例的信噪比損失。

?????????Budge[5]和許多作者已經將這種推理提高到一個更詳細的水平。如果參考信號β(t)在傳遞到拉伸處理器的過程中延遲 $\tau _{M}$ ，則有兩種情況，描述如下。

????????1. $\tau _{M}$ ?> $\tau _{R}$ :在這種情況下，參考信號的頻率比目標回波的頻率低。這意味著拍信號的頻率將低于其實際值，而 $\tau _{M}$ = $\tau _{R}$ 。

????????2. $\tau _{M}$ < $\tau _{R}$ :在這種情況下，參考信號的頻率高于目標回波的頻率。這就意味著當 $\tau _{M}$ = $\tau _{R}$ 時，拍信號的頻率將高于其實際值。這就是圖2.19所示的案例。

????????理想情況下，τM = τR，但這是不現實的。目標延遲和參考延遲將是接近的，大多數分析忽略了這是一個近似值。通常，使用延遲線[1]將參考延遲τM與雷達最近的距離相匹配，因此，幾乎總是τM < τR，且在該特定的距離拍信號會有一個高于正常值的值。然而，這種誤差是可以忽略的。

12.3.1拉伸處理器操作

????????(2.61)是經過低通濾波后的信號，再對其進行復現，

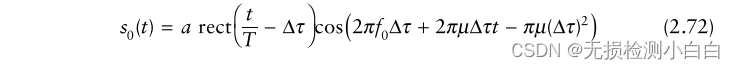
????????我們注意到(2.72)的第一項告訴我們混頻器的輸出是一個與目標范圍成比例的恒頻信號。因此，如果我們確定出混頻器的信號的頻率，我們就可以確定目標范圍。因為，fb = μτR，其中fb是拍頻，我們得到

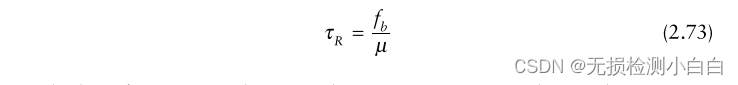
????????拍頻是用頻譜分析儀確定的。頻譜分析儀計算so(t)的傅里葉變換。

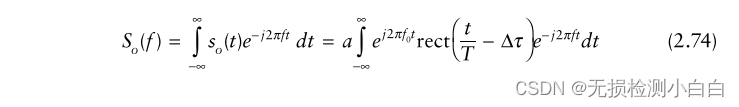
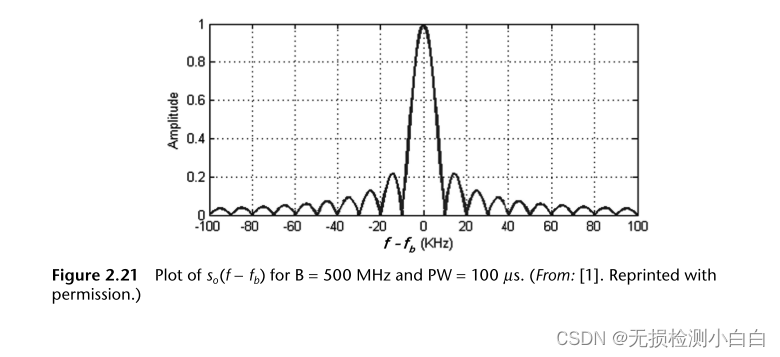
????????或者

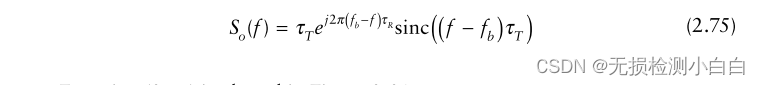
????????式(2.75)繪制在圖2.21中。

????????拉伸處理的距離分辨率是多少? 在圖2.21中，我們注意到脈沖寬度是100μs或10 KHz的倒數。這是sinc函數的標稱寬度。這也是頻譜分析儀的頻率分辨率。假定有一個 τR1 范圍內的靶，另一個τR2 > τR1范圍內的靶。與兩個目標相關聯的混頻器輸出頻率將為

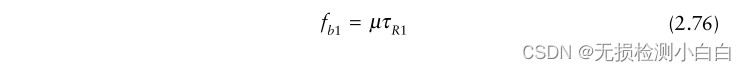
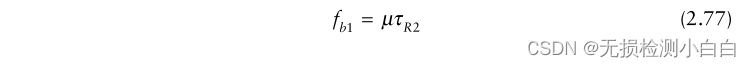
進一步假設 τR1 和 τR2 是這樣的

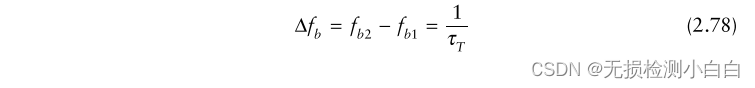
????????拍頻由拉伸處理器的分辨率單元分隔。然后我們可以寫

? ? ? ? ?或者

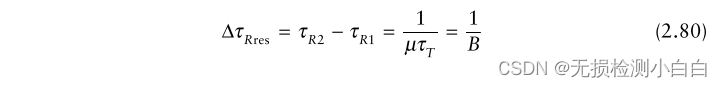
?????????這意味著拉伸處理器具有與匹配的過濾器[6]相同的分辨率。我們通常可以對輸出應用一個加權來減少距離旁瓣。在這種情況下，輸出脈沖寬度的寬度取決于所使用的加權類型。下面將對此進行討論。

????????可證明匹配濾波器的輸出信噪比與雷達距離方程中使用的信噪比相匹配，拉伸處理器的信噪比與匹配濾波器的 τβ/τT 成正比。有興趣的讀者可以向[5]尋求證據。

????????最后，請注意到這一點，我們假設目標是靜態的(即，不移動)。如果目標在移動，它就會產生多普勒頻移在雷達反射頻率中。這一偏移與它的徑向速度成正比，拍頻必須根據這一多普勒偏移進行相應的修正，如本章前面所討論的那樣。

????????關于拉伸加工的更多信息，讀者可以參考[1,2,5,7]。

????????現在我們檢查拉伸處理器的目標解析能力。有一個程序“stretch_processing.M”。我們有四個目標，RCS分別為1、2、1和2，分別位于15、20、23和25米的范圍內。假設有一個漢明窗口。假設發射脈沖寬度T為20ms，帶寬B為1ghz。圖2.22和2.23展示了這種效果。初始頻率為5.6 GHz，接收窗口為60m。

????????1 GHz帶寬的瑞利分辨率是15厘米。作為一個探索性的練習，讀者應該試著將目標的距離控制在15厘米以內。雷達將無法分辨目標，除非掃描帶寬適當地增加。

????????最后，請注意，像聲表面波濾波器這樣的技術通常會產生大約1000的處理增益，而拉伸處理通常會產生50000的增益。這種類型的處理特別適用于高帶寬信號，并利用高達100m的接收窗口。

????????必須記住，這種信號處理——盡管它產生了非常高的脈沖壓縮度(在啁啾脈沖系統中高達50000對1000)——要求接收信號的開始時間是已知的。在啁啾脈沖雷達中，雷達返回的開始時間是未知的，因為它取決于目標位置。來自不同范圍目標的回波具有不同的起始時間，且脈沖持續時間恒定。這使得信號處理變得困難。因此，使用FFT將目標返回值和參考值轉換為頻域是唯一的選擇(相關處理)。然而，在FMCW雷達中，信號是連續的，因此可以方便地應用拉伸處理(在時域工作)。這就是為什么FMCW雷達具有如此高的分辨率(遠高于啁啾脈沖雷達)，也解釋了FMCW雷達的普及。

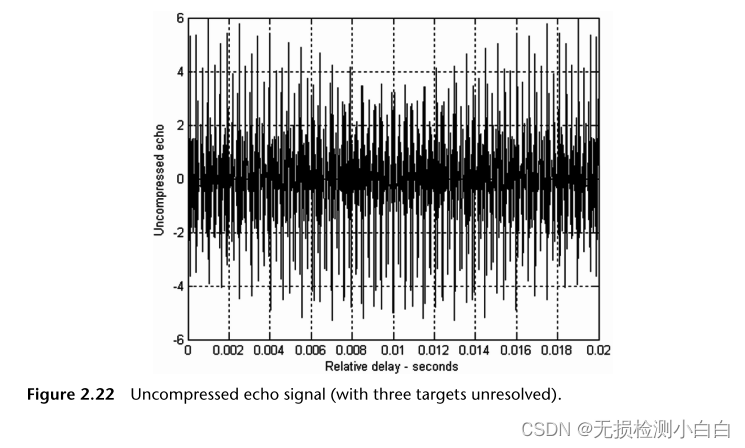
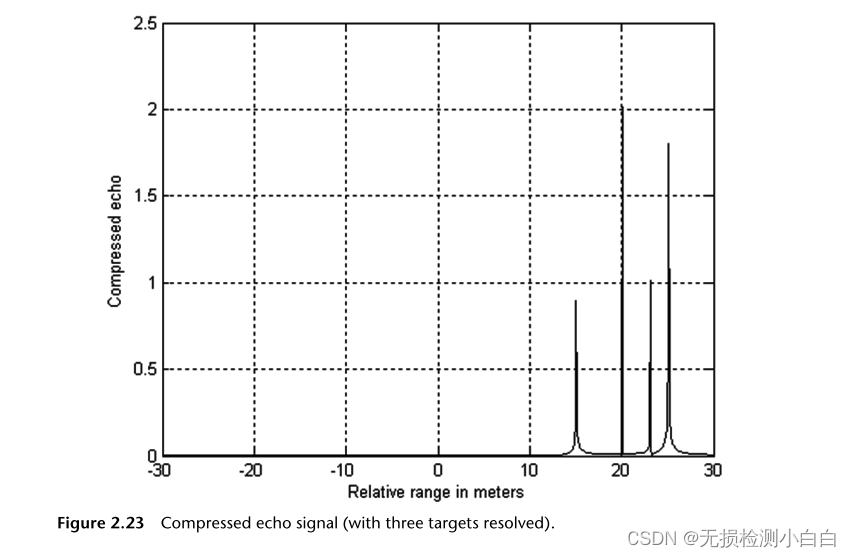
????????來自同一距離單元的所有返回值產生相同的恒定頻率。這種FFT有時也被稱為“距離FFT”，因為它處理的是目標距離。在前面的討論中，我們假設發射的啁啾和接收的啁啾具有相同的斜率。這只在目標是靜態的情況下才成立。如果它有多普勒值，那么接收到的回波將有一個遞增的頻率，這將給拍頻一個穩定的附加頻率差，與目標多普勒成正比。這將導致范圍錯誤。這種現象稱為距離-多普勒耦合，在線性調頻波形中表現突出。第3.3節更詳細地研究了距離-多普勒耦合。另一個原因是，由于目標徑向速度，接收到的脈沖寬度被時間膨脹因子擴大(或壓縮)。這種現象可以通過兩種流行的方式來糾正:

????????1. 我們可以對目標回波進行重復測量，然后確定多普勒值。然后我們調整下一個發射脈沖的啁啾斜率和脈沖寬度，以考慮估計的多普勒頻率和時間膨脹。

????????2. 我們選擇距離單元的寬度，這樣信號不會因為目標多普勒而改變距離單元。雷達設計者總是知道最大預期目標多普勒。通常，我們對測量目標多普勒不感興趣，而只對其距離感興趣。

??????如果要直接測量目標的多普勒，則需要MTD雷達。假設我們有來自同一個目標(在同一個距離bin中)的8個返回值，然后我們將這些返回值路由到一個稱為多普勒FFT的8點FFT。這個FFT的輸出將是目標多普勒，這將在第三部分進行檢查。我們還可以看看圖2.23壓縮后的回波信號(分解了三個目標)。存儲從單一信道返回的8個目標信號，然后將這些信號路由到一個8點多普勒FFT來提取多普勒值。

13? 線性調頻系統的旁瓣和加權

????????由FMCW雷達輸出的單目標截斷正弦波頻譜具有傅里葉理論預測的?sin(x)/x?特征。

????????這種情況下，距離旁瓣僅比主瓣低13.2 dB，這并不令人滿意，因為它會導致附近小目標的遮擋，并將雜波從鄰近的旁瓣引入到主瓣。為了克服匹配濾波器的這種不可接受的特性，時域信號被故意不匹配。這種失配通常以接收信號幅度加權的形式出現。更多信息請參見[1]。

14? FMCW雷達基本方程

?????????FMCW雷達的距離由以下關系[1]計算:????????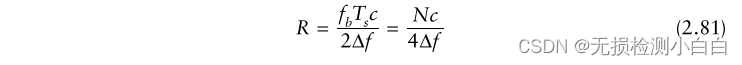

?????????????????R為目標距離;

????????????????Fb是拍頻;

????????????????t為掃描時間;

????????????????Δf是掃頻帶寬或頻率偏移;

????????????????C是光速;

????????????????N為所需的FFT大小(點數)。

????????我們引入了一個新的變量fmax，它是與最大距離對應的最大拍頻。令t = ΔT掃描時間。然后編寫FMCW雷達的最大探測距離為

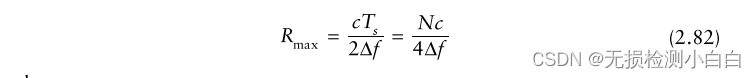
????????????????N為一次掃描時間內的樣本個數;

????????????????fmax = fs / 2，其中fs為滿足奈奎斯特采樣準則的采樣頻率。

????????從前面的章節中我們也知道

????????如果我們現在使用64點FFT和掃描時間Ts = 200 μs和Δf = 10 MHz，我們得到

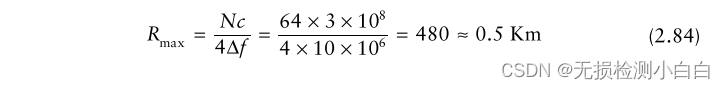
????????在這個最大距離下的距離分辨率由

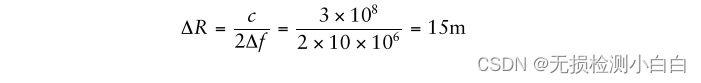
????????在掃頻時間為200 μs，掃頻帶寬為10 MHz的情況下，在0.5 km范圍內實現了15m的距離分辨率。與此相比，使用LFM脈沖的普通脈沖雷達需要壓縮脈沖寬度為100 ns才能實現相同的分辨率。這意味著我們的壓縮比是2000，這是非常高的。這是因為FMCW雷達常見的拉伸處理。讀者還應該注意，在(2.26)中，掃描帶寬在分母中。這意味著整個雷達接收窗口的距離分辨率是恒定的，因為接收窗口中的所有目標都將經歷相同的掃描帶寬。因此，我們可以預期，與脈沖雷達一樣，距離分辨率應該始終是一個常數，而與目標距離無關。然而，在現實中并非如此，因為在FMCW雷達中，距離分辨率是以下函數的函數:

? ? ? ? ? ? ? ?掃描時間;

? ? ? ? ? ? ? ? 非線性

????????為了在一次掃描中產生64個樣本(即進行64點FFT)，采樣頻率

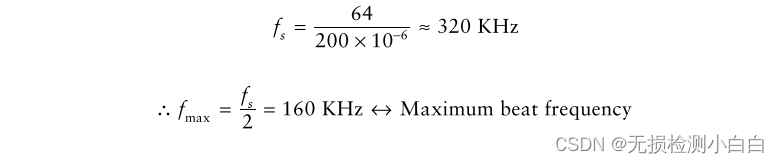
????????因為我們有64個采樣/掃描，所以我們使用64點FFT來確定距離。然而，實采樣的光譜是對稱的。因此，我們只需要使用光譜的一半(即在我們的示例中為32)。因此，距離單元格的數量是32。然而，我們需要處理兩個頻譜的一半，否則我們將失去一半的功率(即，我們進行復雜的處理)[1]。

14.1 FMCW方程

????????頻率偏差、調制周期、拍頻和轉換時間之間有直接關系。這種關系稱為FMCW方程[1]。

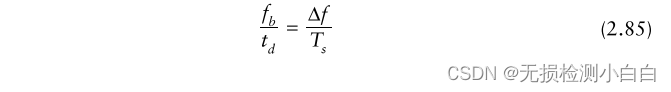
????????????????Fb是拍頻

????????????????td是往返傳播時間延遲= 2R/c，其中R是到目標的距離

????????????????Δf是掃描帶寬或頻率偏差

?????????????????Ts為調制周期(掃描時間)

????????鑒于距離-多普勒耦合固有的線性調頻波形態如前所述，上掃的拍頻取決于距離和速度。

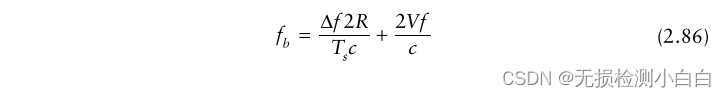
????????????????V 為目標相對于雷達的速度(即徑向速度)

? ? ? ? ? ? ? ? f 為標稱雷達頻率

????????(2.86)中的第二個表達式構成了目標的多普勒頻移。為了解決這種耦合，我們需要有兩個頻率轉換速率或斜率。或者，將距離-多普勒耦合控制在一個距離單元內。

15??FMCW雷達距離方程重估

????????雷達的距離是由

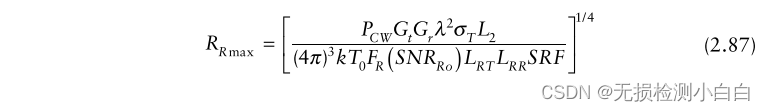
????????我們用輸出信噪比和掃描重復頻率來表示雷達距離方程。式(2.87)和(1.15)是該方程最常用的形式。就像在低噪聲放大器(LNA)的輸入端測量輸入信噪比一樣，輸出信噪比在最終中頻濾波器(標記RF級的末端)的輸出端或范圍FFT的輸出端測量。(這意味著距離FFT的處理增益也被考慮在內。)

16? 掃描時間對距離分辨率的影響

????????到達目標和返回的總時間延遲由兩個因素[1?3]造成，如下所示(見圖2.24):

????????????????1. 往返傳播延遲到最大距離;

????????????????2. 掃描恢復時間Tsr。這是在一次掃描結束和下一次掃描開始時所經過的時間。因此，如果Ts是掃描周期:

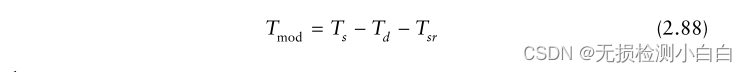
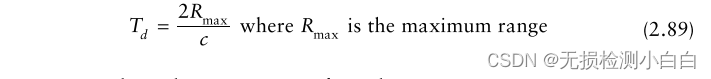
????????因此，在我們獲得最大范圍的返回值之前，我們無法處理范圍fft。這將導致Δfeff給出的有效處理帶寬減少

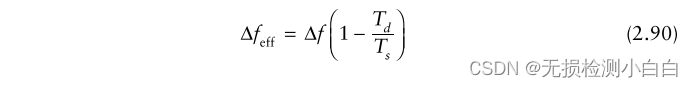
????????因此，降級的距離分辨率ΔRdeg由

????????例1

????????現在我們使用一個示例來更好地解釋流程[1]。假設我們有以下參數:

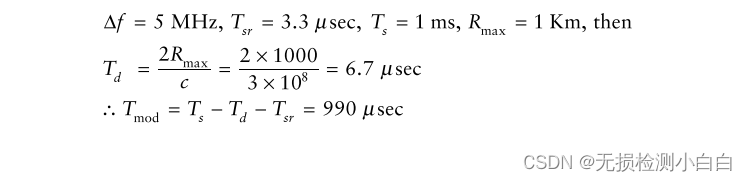
????????6.7 μs的切換時間加上3.3 μs的掃描恢復時間使掃描帶寬減少了0.05 MHz。這使得有效傳輸帶寬為4.95 MHz。

????????理想的距離分辨率是

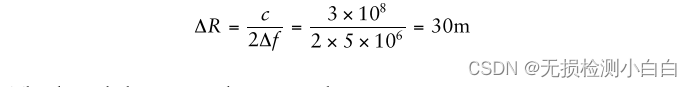
????????降級的距離分辨率現在變成

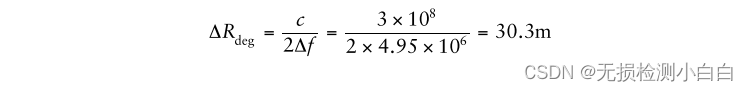
????????這是最壞的情況(即，在最大距離下，距離分辨率是最小的)。它在近距離變得越來越好，因為Td值隨著我們靠近雷達而減小。因此，通常情況下，調制周期Ts至少保持在最大范圍內傳輸時間的5倍，因此有效處理帶寬至少是總帶寬的80%[2,3]。

17? 儀器量程的概念

????????通常，雷達距離方程(2.87)和(1.22)給出的是雷達的能量范圍。在給定發射機功率水平和其他雷達參數，以及目標類型和傳播條件的情況下，這是一個人可以達到的距離。然而，我們通常允許顯示上的雷達距離刻度稍微超出這個能量范圍，通常多出30%。這個距離稱為雷達儀表距離。這是雷達設計的覆蓋范圍(也就是說，它是儀器化的)。例如，一種雷達的能量范圍可能是2公里，但儀器的距離可能是3公里。理想情況下，設計師應該努力使儀器測量范圍盡可能接近能量范圍，否則這是毫無意義的，因為雷達不會探測到超過能量范圍的東西。換句話說，雷達接收窗口變得過多。這將導致提供更高的拍頻，從而更高的中頻濾波器帶寬，比通常可以預期的基于雷達規格。這反過來又需要更高的采樣頻率。因此，應盡量避免過大的儀器測量范圍。

18? 非線性調頻波形

????????為了說明這個問題，我們利用(2.87)根據以下參數確定最大距離(也稱為能量距離):

????????所需距離分辨率:

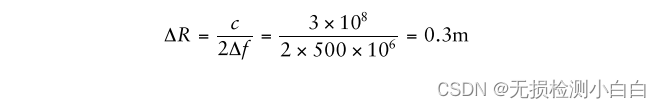
????????雷達參數為

????????使用(2.91)，我們實現了一個2平方米目標的能量距離Rmax為993米。

????????該雷達的拍頻由

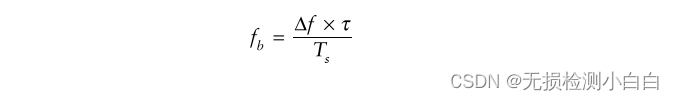
????????此Rmax的往返傳播時間為6.62 μs。

????????因此，

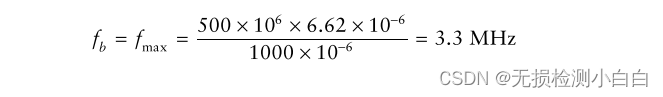
????????這產生3.3 mhz /993m或3323.3 hz /m拍頻率范圍比(比例因子，SF)。

????????這種雷達的理想距離分辨率是

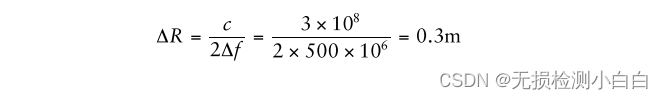
????????因此0.3 m距離分辨率需要996.98-Hz的接收頻率分辨率，因此頻率掃描線性為500-MHz頻率偏差的0.0002%。因此，這是需要的線性，以達到我們期望的0.3m的距離分辨率。讀者可以驗證較高的非線性，例如0.04%不滿足我們的要求。

????????這使得我們可以使用數字FMCW發生器，比如DDS[1]。這種發生器在掃描的末端不會有不連續，因為掃描的末端是門控的。這種方法叫做消隱。

19? 相干處理間隔

? ? ? ? 我們需要確定距離FFT的大小。我們將經過處理的采樣與調制周期進行匹配，條件是采樣的個數為2的冪。這就產生了

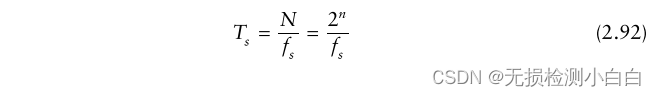
????????其中 $N = 2^{n}$ 是采樣，所以

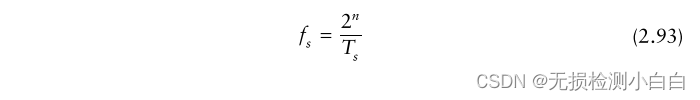
????????利用FMCW方程(2.85)，我們可以通過重新排列這些項，用拍頻來表示距離。

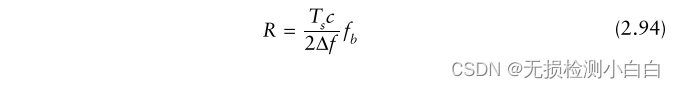
????????我們知道最大拍頻

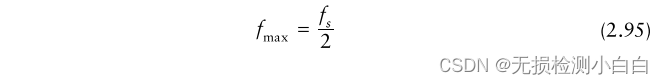
????????將(2.95)代入fmax，得到

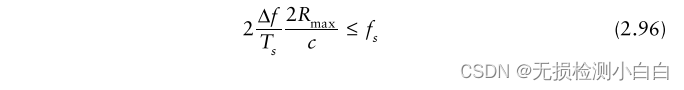
????????利用第18節的例子結果，我們得到fmax = 3.3 MHz。因此，fs必須至少是6.7 MHz。

????????現在將(2.93)代入(2.96)得到

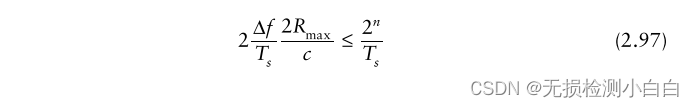
????????所以

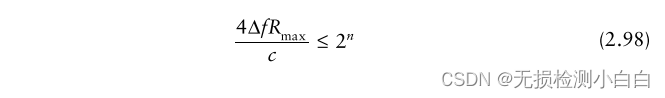
????????再一次，使用2.18節中的例子，(2.98)的左邊是6,620，所以右邊必須是8,192或 $2^{13}$ ; 8192個采樣在1毫秒內對應8.192兆赫茲采樣頻率。8192點FFT將覆蓋高達4.096 MHz的拍頻，對應距離高達1232米。拍頻采樣間隔為1khz，對應的距離間距為0.3m。漢明窗的頻率分辨率等于6 db帶寬1.81乘以1 KHz頻率采樣間隔或1.81 KHz，在距離內對應0.545m。

20? 小結

????????本章研究了FMCW雷達的基本設計理論，檢驗了FMCW雷達的方程。研究了目標多普勒對雷達性能的影響及其測量方法。接下來，本章研究了FMCW雷達距離方程，并從輸出信噪比和掃頻重復頻率(而不是掃頻帶寬)的角度推導出了它的新形式。這種形式在FMCW雷達設計中得到了廣泛的應用。隨后，我們研究了影響距離分辨率的因素(例如，掃描次數和拍頻分辨率)，特別是像目標返回光譜寬度和接收機頻率分辨率這樣的問題，它們在決定拍頻分辨率方面起著關鍵作用，從而導致最終的接收機距離分辨率。最后，通過實例，本章討論了FMCW波形的非線性問題及其控制。這需要在雷達沒有過度儀表化的距離的情況下完成。