435. 無重疊區間

我認為區間類的題型，大多數考驗的是思維能力，以及編碼能力，該類題型本身并無什么算法可言，主要是思維邏輯，比如本題實際上你只需要能夠總結出重疊與不重疊的含義，再加上一點編碼技巧，便可完成。

解題思路

正如前面所說，那么解題的關鍵思路就在于找到重疊區間的特性即可，我們不妨先按照start進行一次排序，再進行觀察，比如數組：[[1,2],[2,3],[3,4],[1,3]]，排序后為：[[1,2],[1,3],[2,3],[3,4]]，通過觀察我們很容易發現，如果前一個數組的end大于下一個數組的start，則這兩個數組一定發生了重疊，這個比較容易理解，如圖所示：分別有兩個數組[1,2]和[1,3]

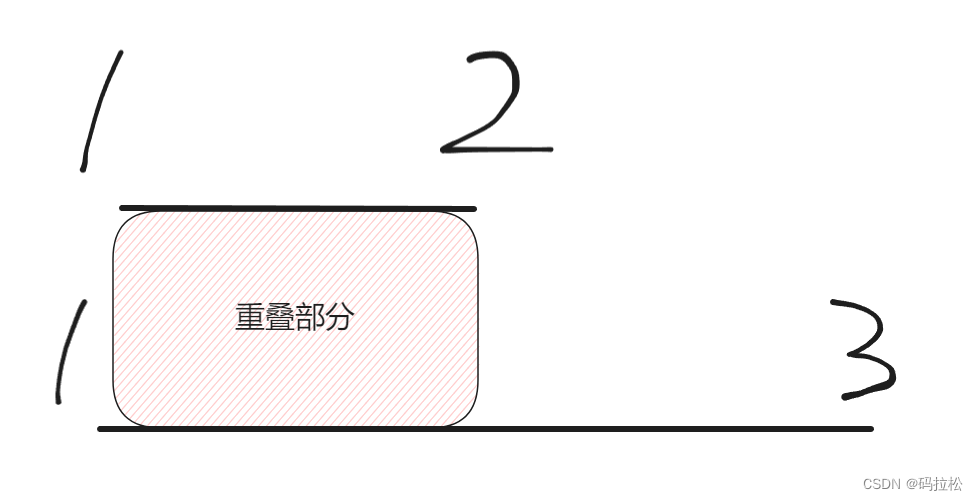
重疊部分一眼可見，但關鍵在于產生重疊后，應該留下誰？舍棄誰？我們不妨還是畫圖理解，按照題目示例，接下來一組數字是[2,3]

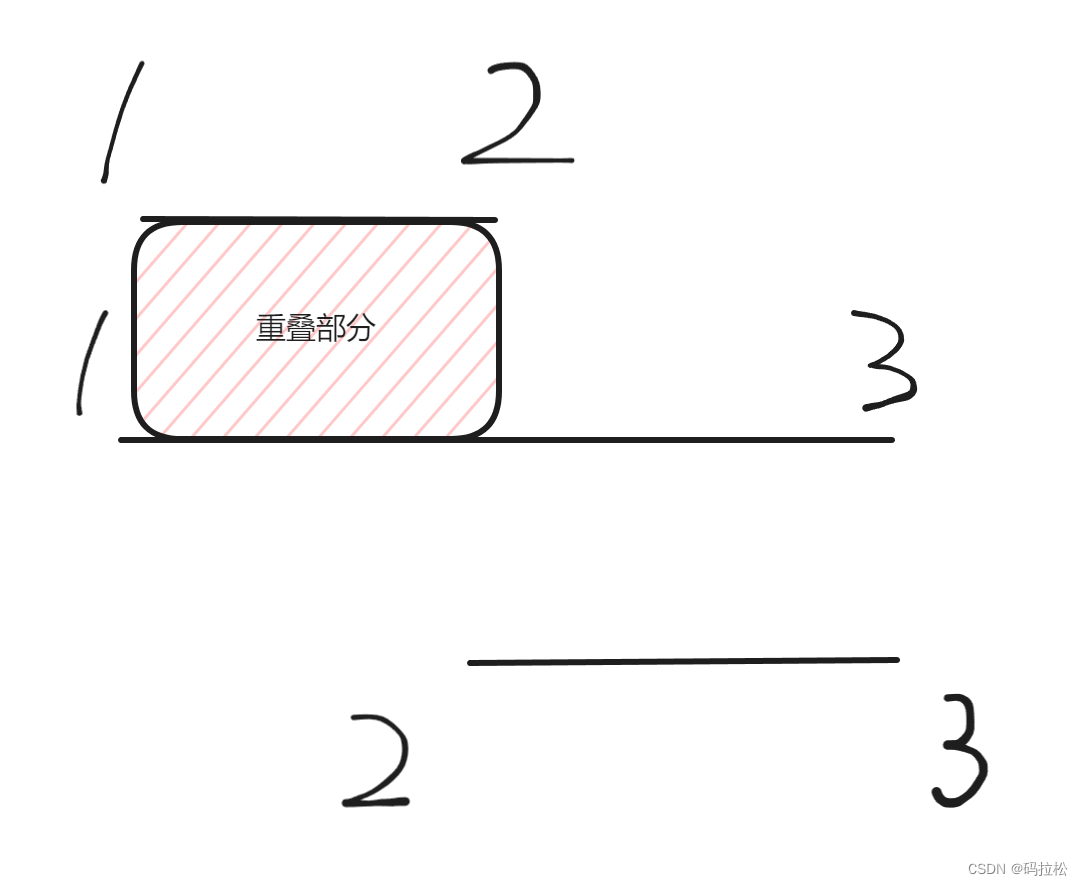
我們可以分開討論，假設我們選擇保留[1,3]，那么很明顯下一組[2,3]將變為重疊部分。

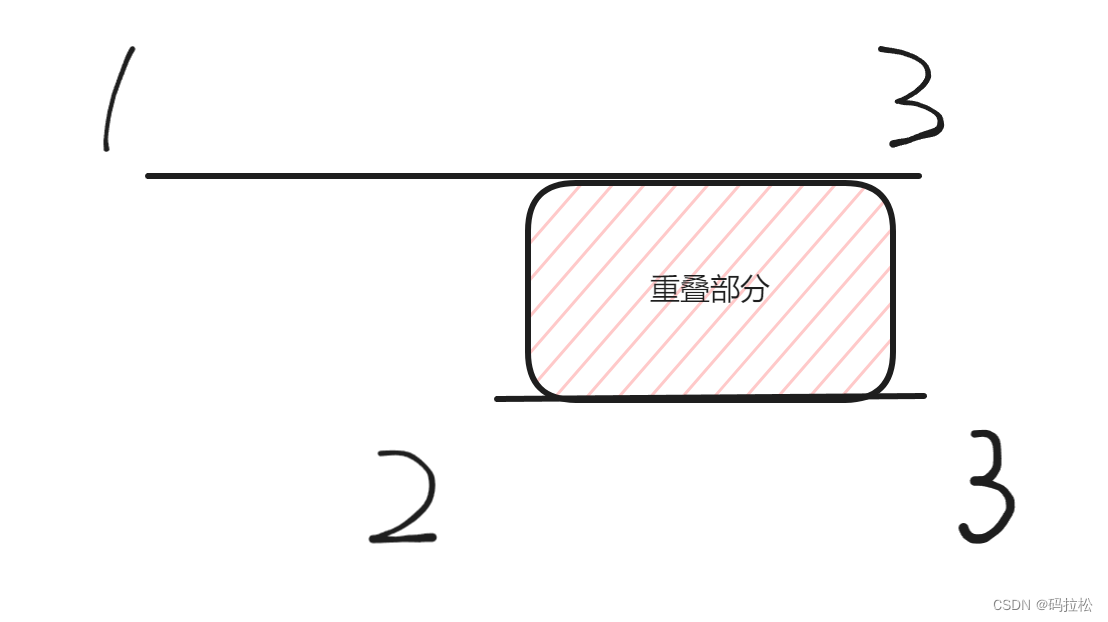
而如果我們選擇保留[1,2]，則不會再產生重疊部分。

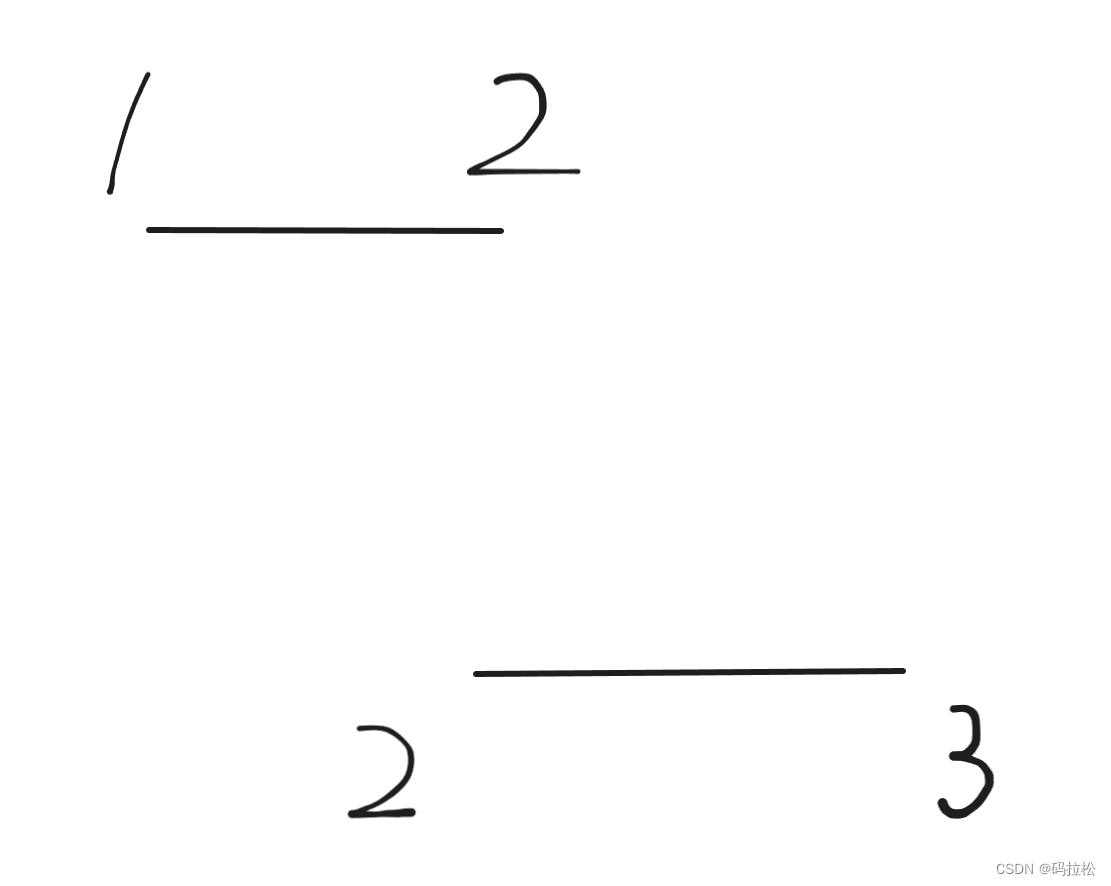
根據題目要求，需要我們通過移除最少的區間數量來實現區間互不重疊，因此應當使用第二種方案，從原理上來說，就是當兩個區間產生重疊后，我們應當保留區間范圍更小的一組，因為這樣更有可能避免與后面的區間再產生重疊（很容易理解的一點概念：區間范圍越大，越容易發生重疊）

結論，假設有[[s1, e1], [s2, e2], [s3, e3] ... [sn, en]]，如果e1 > s2，則將觸發[s1 ,e1],[s2, e2]合并，合并規則為：如果e1 > e2，合并為[s1, e2]，否則合并為[s1, e1]，如果e1 <= s2，則無需合并，直接檢查下一個區間即可。

代碼實現

public int eraseOverlapIntervals(int[][] intervals) {// 不要忘了，先按start進行排序Arrays.sort(intervals, (o1, o2) -> o1[0] - o2[0]);int ans = 0;int end = intervals[0][1];for(int i = 1; i < intervals.length; i++){int start = intervals[i][0];if(end > start){end = Math.min(end, intervals[i][1]);ans++;}else{end = intervals[i][1];}}return ans;
} 

56. 合并區間

解題思路

本題與上一題比較相似，都是處理重疊區間的問題，我們同樣可以畫圖理解，以題目示例1為例：[[1,3],[2,6],[8,10],[15,18]]。

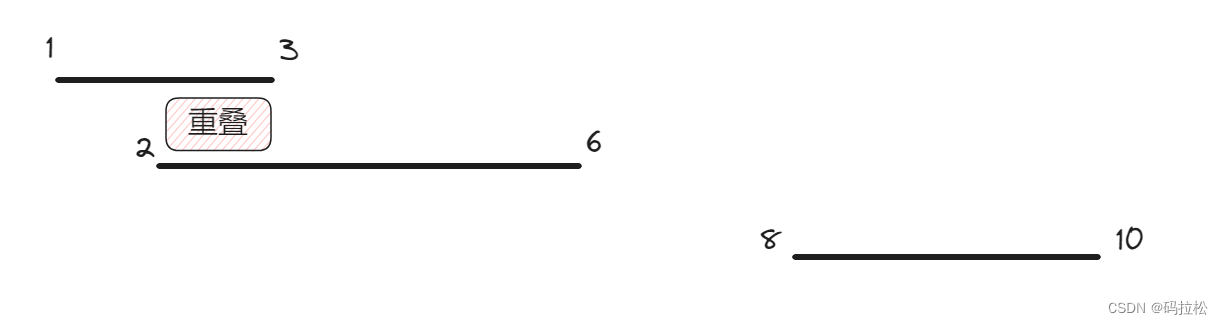
首先與前一題一樣，如果前一個數組的end大于下一個數組的start，則表示一定出現了重疊，而關于end部分的去留，則正好與前一題相反，前一題保留的是較小部分，本題則需要保留較大部分。

結論，假設有[[s1, e1], [s2, e2], [s3, e3] ... [sn, en]]，如果e1 >= s2，則將觸發[s1 ,e1],[s2, e2]合并，合并規則為：如果e1 > e2，合并為[s1, e1]，否則合并為[s1, e2]，如果e1 < s2，則無需合并，直接檢查下一個區間即可。

代碼實現

由于本題需要在原數組上進行修改，因此先借用一個list輔助記錄，實際處理邏輯并沒區別。

class Solution {public int[][] merge(int[][] intervals) {Arrays.sort(intervals, (o1, o2) -> o1[0] - o2[0]);List<int[]> list = new ArrayList<>();list.add(new int[]{intervals[0][0], intervals[0][1]});for(int i = 1; i < intervals.length; i++){int start = intervals[i][0];int end = intervals[i][1];if(list.get(list.size()-1)[1] < start){list.add(new int[]{start, end});}else{list.get(list.size()-1)[1] = Math.max(end, list.get(list.size()-1)[1]);}}return list.toArray(new int[list.size()][]);}
}

1288. 刪除被覆蓋區間

解題思路

前面兩題處理的都是數據范圍重疊的問題，本題要解決的則是數據范圍覆蓋問題，我們先要搞清楚符合覆蓋的條件有哪些？很明顯，當s1 <= s2 且 e2 <= e1時，則認為[s2, e2]區間被[s1, e1]區間覆蓋。

如下圖所示：

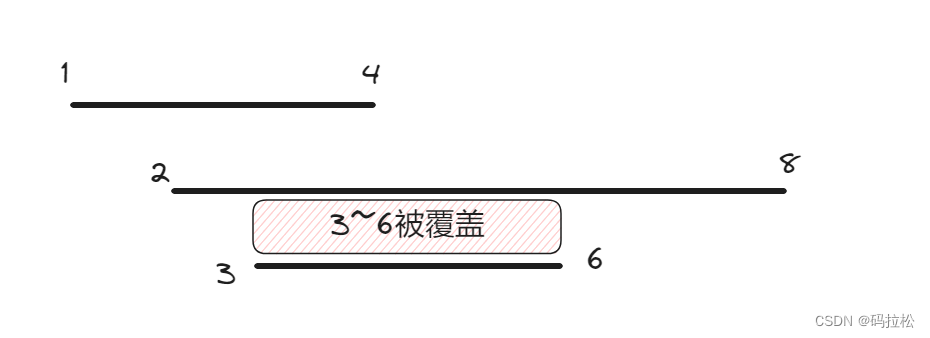
結論，假設有[[s1, e1], [s2, e2], [s3, e3] ... [sn, en]]，當s1 <= s2 且 e2 <= e1時，則可刪除區間[s2, e2]，這里需要注意的是，為了方便處理，我們可以讓start按照升序排序的同時，并讓end按照降序排序，這樣代碼實現時只要滿足e1 >= e2即可認為被覆蓋了。實際上就是為了方便進行判斷s1 <= s2 且 e2 <= e1

代碼實現

class Solution {public int removeCoveredIntervals(int[][] intervals) {Arrays.sort(intervals, (o1, o2) -> o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0]);int cnt = 0;int preEnd = intervals[0][1];for (int i = 1; i < intervals.length; i++) {int curEnd = intervals[i][1];if (preEnd >= curEnd) {cnt++;} else {preEnd = curEnd;}}return intervals.length - cnt;}
}