題目
測試鏈接
在一條環路上有 n 個加油站,其中第 i 個加油站有汽油 gas[i] 升。
你有一輛油箱容量無限的的汽車,從第 i 個加油站開往第 i+1 個加油站需要消耗汽油 cost[i] 升。你從其中的一個加油站出發,開始時油箱為空。
給定兩個整數數組 gas 和 cost ,如果你可以按順序繞環路行駛一周,則返回出發時加油站的編號,否則返回 -1 。如果存在解,則 保證 它是 唯一 的。
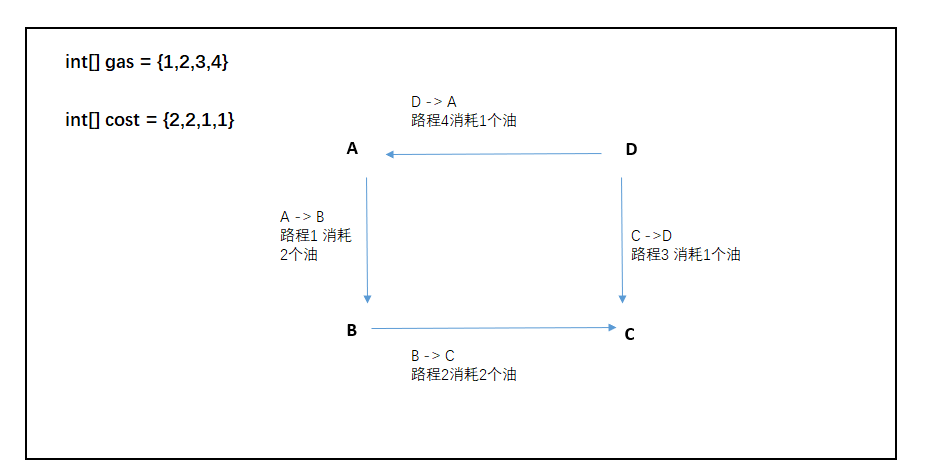
解釋一下這道題,如下圖所示:
路程數組gas和油耗數組cost,假設從A點出發,走到B點路程為1,消耗油量為2,1 - 2 = -1,油量不夠支撐走到B點,所以如果從A點出發,無法完整的繞完一圈,B、C、D同理,這道題就是看從哪個出發點出發后,可以順利的繞完一圈(gas和cost等長)。
滑動窗口
首先,先將給定的 gas[] 和 cost[] 稍稍加工一下,一次遍歷,用gas[i] - cost[i],得到的新數組中包含正負數,就是從每個點出發的路程和油耗的差值,看是否有能力到達下一個目的地。
此時如果用暴力方法解這道題的話,只需要從0 ~ N - 1每個位置循環遍歷,遍歷N個位置。看過程中是否出現負數,如果是負數,則說明不能完成循環,如果不是,結果 >= 0,則證明可以完成循環。
我們這里直接說用滑動窗口的解題思路:
依然是先加工gas[] 和 cost[],不同的是,我們要根據加工出來的gas[] - cost[],搞出來一個2倍gas[]長度的前綴和數組。
因為我們要看從 0 ~ N - 1位置中每個的出發點能否成功繞回來, gas[] - cost[] 加工出來的數組就是從每個點出發能否成功到達下一目的地的數組,所以當累加到N - 1位置時,下一步重新在加上 0 位置的值,來構造出這個2倍長度累加和數組。
這樣的做的目的是,我下圖中 double.length中下標4的位置,可以看做是從B點出發,又重新繞回A的0位置,下標5的位置,可以看做是從C點出發,重新繞回B點的1位置。一個數組全部可以搞定。
所有原始數組中出發的位置,在double.length中都可以將原始數組的累加和數組加工出來。
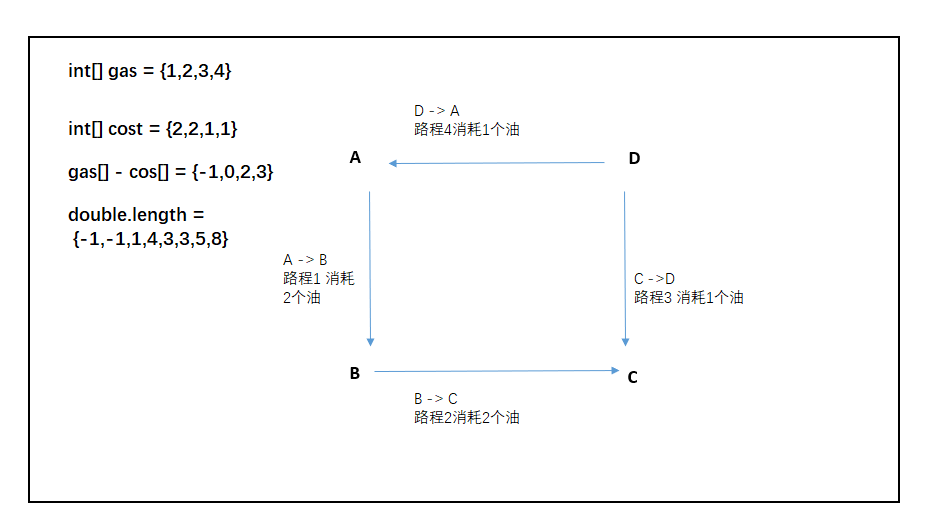
怎么加工?
假設我從D點出發,那么在gas - cost中求出來的累加和數組就是{3,2,2,4}(因為要重新往A點加繞回來),對應在double.length中就是劃線部分,怎么得出來的呢?
劃線數組中的每一個數,都減去劃線部分的前一個數(1)。
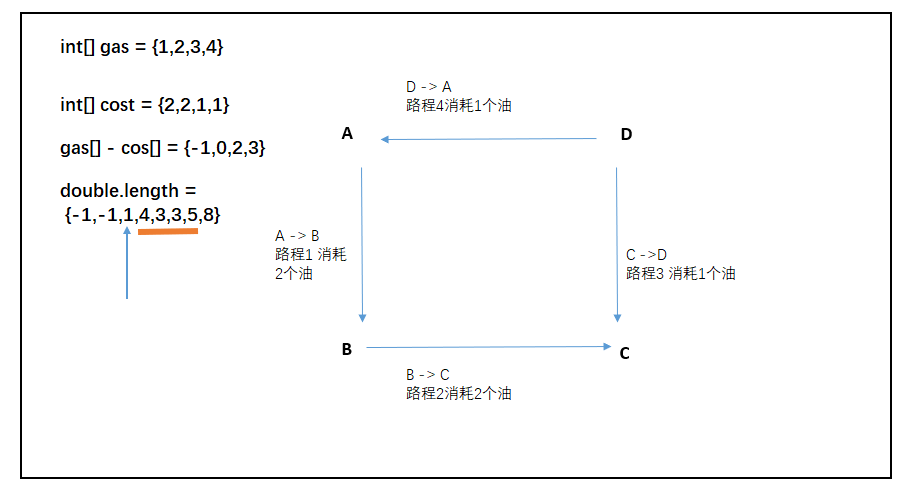
所以,綜上所述,此時我們維護一個窗口最小值,窗口范圍就是gos.length,每次窗口變化后,根據窗口內最小值 - 前一個值,如果此時已然 < 0,則說明該位置不是最佳出發點。否則就認為是最佳出發點。
代碼
public static int canCompleteCircuit(int[] gas, int[] cost) {boolean[] booleans = goodArray(gas, cost);for (int i = 0; i < booleans.length; i++) {if (booleans[i]) {return i;}}return -1;}public static boolean[] goodArray(int[] gas, int[] cost) {int N = gas.length;int M = N << 1;int[] arr = new int[M];for (int i = 0; i < N; i++) {arr[i] = gas[i] - cost[i];arr[N + i] = gas[i] - cost[i];}for (int j = 1; j < M; j++) {arr[j] += arr[j - 1];}LinkedList<Integer> w = new LinkedList<>();for (int i = 0; i < N; i++) {while (!w.isEmpty() && arr[w.peekLast()] >= arr[i]) {w.pollLast();}w.addLast(i);}boolean[] ans = new boolean[N];for (int offset = 0, i = 0, j = N; j < M; offset = arr[i++], j++) {if (arr[w.peekFirst()] - offset >= 0) {ans[i] = true;}if (w.peekFirst() == i) {w.pollFirst();}while (!w.isEmpty() && arr[w.peekLast()] >= arr[j]) {w.pollLast();}w.addLast(j);}return ans;}




)


的初步介紹)




)






