文章目錄
- 前言
- 一、OFDM 信號及模糊函數
- 1、OFDM 信號表達式
- 2、模糊函數表達式
- 二、MATLAB 仿真
- 1、MATLAB 核心源碼
- 2、仿真結果
- ①、OFDM 模糊函數
- ②、OFDM 距離模糊函數
- ③、OFDM 速度模糊函數
前言
本文進行 OFDM 的仿真，首先看一下 OFDM 的模糊函數仿真效果：
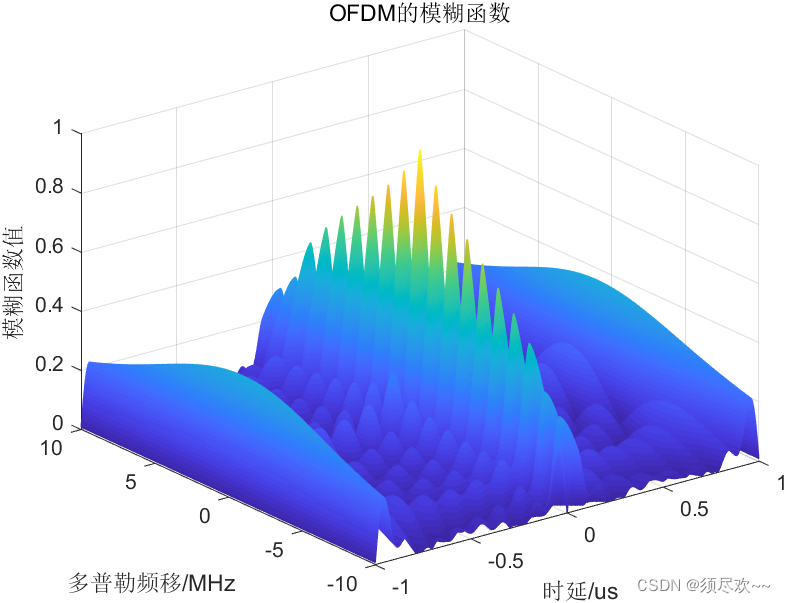
一、OFDM 信號及模糊函數
1、OFDM 信號表達式
OFDM 信號提供了一種在頻域上設計波形、時域上輸出波形的 DFT 數字調制方式。OFDM 信號的數學表達式為：
B ( t ) = ∑ k = 0 N ? 1 b k e j 2 π f k t = ∑ k = 0 N ? 1 b k e j 2 π ( f 0 + k Δ f ) t B(t)=\sum_{k=0}^{N-1}b_ke^{j2\pi f_kt}=\sum_{k=0}^{N-1}b_ke^{j2\pi (f_0+k\Delta f)t} B(t)=k=0∑N?1?bk?ej2πfk?t=k=0∑N?1?bk?ej2π(f0?+kΔf)t
- b k ：調制序列，為第 k 路子信道中的復輸入數據 b_k：調制序列，為第 k 路子信道中的復輸入數據 bk?：調制序列，為第k路子信道中的復輸入數據
- f k = f 0 + k Δ f f_k=f_0+k \Delta f fk?=f0?+kΔf， f 0 f_0 f0? 為起始頻率， Δ f \Delta f Δf 為頻率間隔
2、模糊函數表達式
模糊函數是雷達探測波形分析的重要工具，通過對信號波形的模糊函數分析，可以得到信號波形的距離分辨率、多普勒分辨率及多普勒容限特性。
為了分析在不同的時延和多普勒頻移條件下接收信號與匹配濾波器的不匹配程度，定義了模糊度函數。
連續時間信號模糊函數的定義為：
χ ( τ , f d ) = 1 E ∫ ? ∞ ∞ b ( t ) b ? ( t ? τ ) e j 2 π f d t d t \chi (\tau,f_d)=\frac{1}{E} \int_{-\infty}^{\infty} b(t)b^{*}(t-\tau)e^{j2\pi f_dt} \,dt χ(τ,fd?)=E1?∫?∞∞?b(t)b?(t?τ)ej2πfd?tdt
- 式中，E為信號的總能量；
離散時間序列的模糊函數表示為：
χ ( m , k d ) = 1 E c ∑ n e n e n ? m ? e j 2 π N k d n \chi (m,k_d)=\frac{1}{E_c}\sum_{n}e_ne^{*}_{n-m}e^{j\frac{2\pi}{N}k_dn} χ(m,kd?)=Ec?1?n∑?en?en?m??ejN2π?kd?n
- 式中， m = f s × τ m=f_s×\tau m=fs?×τ， f s f_s fs? 為采樣率；
- k d = f d × f s N k_d=\frac{f_d×f_s}{N} kd?=Nfd?×fs??，N為采樣點數
二、MATLAB 仿真
1、MATLAB 核心源碼
%% ofdm信號產生
for j = 0:N_symbol - 1 % 用于處理每個相位編碼for k = 0:M-1 % 用于處理每個子載波for n = 0:N-1 % 用于生成每個時刻的樣本x_tmp(k+1,n+1+j*N) = tx_data(k+1+j*N)*exp(1j*2*pi*k*n/N);endend
end
2、仿真結果
①、OFDM 模糊函數
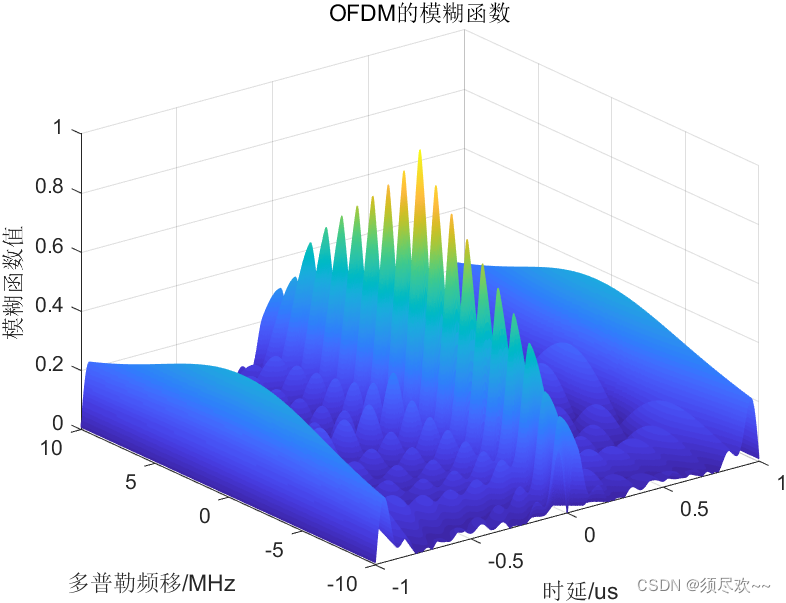
②、OFDM 距離模糊函數
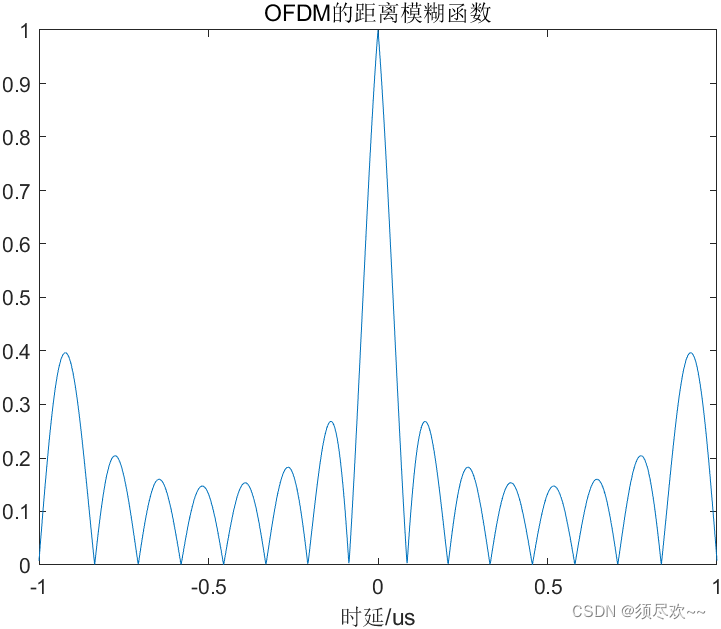
③、OFDM 速度模糊函數
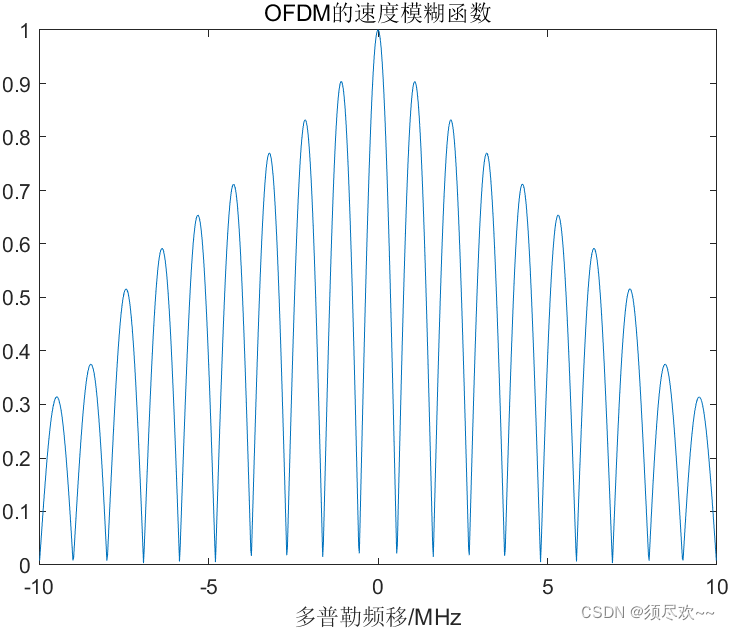
我的qq：2442391036，歡迎交流！
