dp
1、343. 整數拆分
題目：
給定一個正整數 n ，將其拆分為 k 個 正整數 的和（ k >= 2 ），并使這些整數的乘積最大化。
返回 你可以獲得的最大乘積 。
輸入: n = 10
輸出: 36
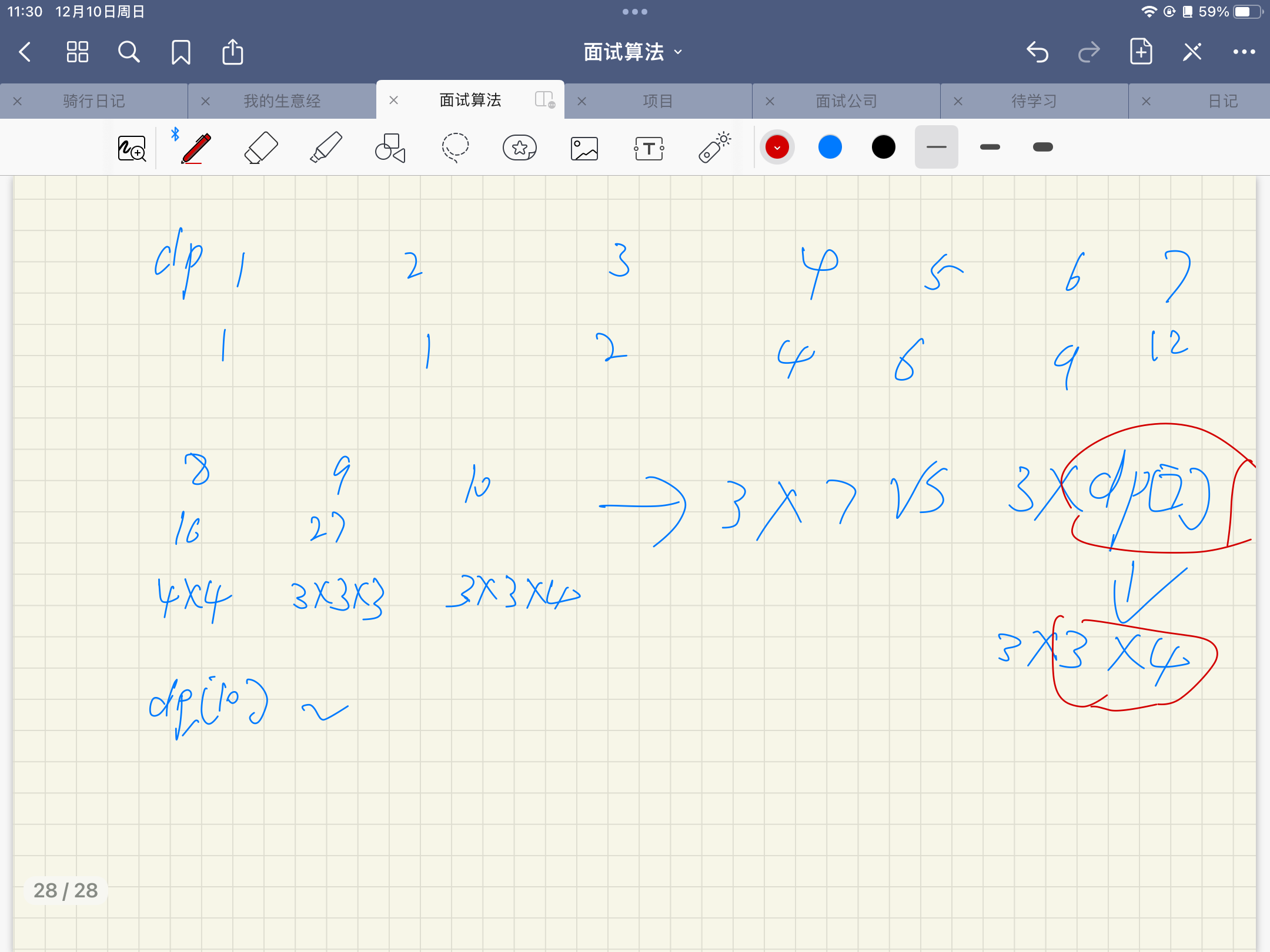
解釋: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
思路：
- 老辦法，畫圖理解
- 10是如何分為334，343，433，呢？這都是最大的值27，例如，i=3的時候，在遞推公式有一個jdp[i-j]，就是這一步，實現了334 or 343，因為dp[i-j] = dp[7] = 34 or 4*3
- 普及一個概念，在相同的總和下，例如長寬高，最近圓形的最完美，所得之積最大，體積也是如此，例如球形，這是我在初二左右時候寫數學題悟出來的
func integerBreak(n int) int {// 理解了寫dp := make([]int, n+1)dp[1]=1dp[2]=1for i:=3;i<n+1; i++ {for j:=1; j<i; j++ {dp[i] = max(dp[i], max(j*(i-j),j*dp[i-j]))}}return dp[n]
}
func max(a, b int) int {if a>b {return a}; return b}
2、96. 不同的二叉搜索樹
題目：
給你一個整數 n ，求恰由 n 個節點組成且節點值從 1 到 n 互不相同的 二叉搜索樹 有多少種？返回滿足題意的二叉搜索樹的種數。
輸入：n = 3
輸出：5
思路：
- i代表dp[i]有多少個不同的二叉搜索樹，j代表頭節點為j
- 同時是考慮了二叉搜索樹特性的情況
func numTrees(n int) int {// 代碼一刷，卡哥視頻講的很好，容易理解的dp := make([]int, n+1)dp[0] = 1for i:=1; i<n+1; i++ {for j:=1; j<=i; j++ {dp[i] += dp[i-j]*dp[j-1]}}return dp[n]
}
