題目描述：

如果Z既是X的子串，又是Y的子串，則稱Z為X和Y的公共子串。

如果給定X、Y，求出最長Z及其長度。

注意：這里求的不是子序列，兩者的意思并不相同。子串要求連續，子序列并不需要。

如果想要了解可以看這一篇最長子序列問題（LCS）--動態規劃解法

示例：

輸入

ABACCB

AACCAB

輸出

ACC

3

分析：

dp[i][j]表示X從0到i與Y從0到j之間公共子串的長度。

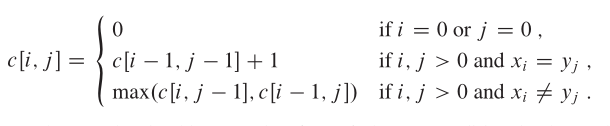
代碼：

?

//最長字串問題,不是最長子序列問題
#include<iostream>
#include<string>
using namespace std;const int N = 1000;
int dp[N][N] = { 0 };int  main()
{string a, b;cin >> a;cin >> b;int lena = a.size();int lenb = b.size();int maxLen = 0;//最長字串長度int start = 0;//最長字串在a中的初始下標//本來要將dp[i][0]和dp[0][j]全都初始化，但是因為是0，所以可以省略//直接dpfor (int i = 0; i <lena; i++){for (int j = 0; j <lenb; j++){if (a[i] == b[j]){if (i > 0 && j > 0){dp[i][j] = dp[i - 1][j - 1] + 1;}else{dp[i][j] = 1;}}//如果a[i]!=b[i]，則dp[i][j] = 0//這是因為子串要連續，走到i,j就斷了這個連續。else{dp[i][j] = 0;//這步可以省略，因為初始值就是0；}if (dp[i][j] > maxLen){maxLen = dp[i][j];//更新最長字串長度start = i - maxLen + 1;//記錄最長字串在a中的初始下標}}}cout << "dp數組為：" << endl;for (int i = 0; i < lena; i++){for (int j = 0; j < lenb; j++){cout << dp[i][j] << ' ';}cout << endl;}cout << "最長子串長度為：" << maxLen << endl;cout << "最長子串為" << a.substr(start, maxLen) << endl;system("pause");return 0;}