【數據結構(九)】線索化二叉樹（3）

文章目錄

  • 1. 前言——問題引出
  • 2. 線索二叉樹的基本介紹
  • 3. 線索二叉樹的應用案例
    • 3.1. 思路分析
    • 3.2. 代碼實現
  • 4. 遍歷線索化二叉樹
    • 4.1. 代碼實現

1. 前言——問題引出

????

問題：
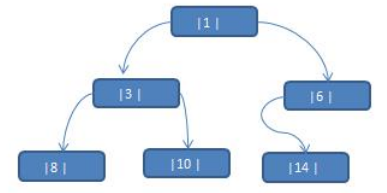
????將數列 {1, 3, 6, 8, 10, 14 } 構建成一顆二叉樹. （n+1=7個空指針域）

在這里插入圖片描述
????

問題分析:
1.當對上面的二叉樹進行中序遍歷時，數列為 {8, 3, 10, 1, 6, 14 }
2.但是 6 的 右指針，8、10、14 這幾個節點的 左右指針，并沒有完全的利用上（共7個空指針域）
3.如果希望充分的利用 各個節點的左右指針，讓各個節點可以指向自己的前后節點，怎么辦?
????
解決方案：線索二叉樹

2. 線索二叉樹的基本介紹

在這里插入圖片描述

  1. n n n 個結點的二叉鏈表中含有 n + 1 n+1 n+1 【公式 2 n ? ( n ? 1 ) = n + 1 2n-(n-1)=n+1 2n?(n?1)=n+1】 個空指針域。利用二叉鏈表中的空指針域，存放指向該結點在某種遍歷次序下的前驅和后繼結點的指針（這種附加的指針稱為"線索"）。
  2. 這種加上了線索的二叉鏈表稱為線索鏈表，相應的二叉樹稱為線索二叉樹(Threaded BinaryTree)。根據線索性質的不同，線索二叉樹可分為前序線索二叉樹、中序線索二叉樹和后序線索二叉樹三種。
  3. 一個結點的前一個結點，稱為前驅結點。
  4. 一個結點的后一個結點，稱為后繼結點。

3. 線索二叉樹的應用案例

應用案例說明：
????將下面的二叉樹，進行中序線索二叉樹。中序遍歷的數列為 {8, 3, 10, 1, 14, 6}

在這里插入圖片描述

3.1. 思路分析

中序遍歷的結果：{8, 3, 10, 1, 14, 6}

在這里插入圖片描述

說明:
當線索化二叉樹后，Node節點的 屬性 left 和 right ，有如下情況:
（1）left指向的是左子樹，也可能是指向的前驅節點，比如 “1節點” 的left 指向的左子樹, 而 “10節點” 的 left 指向的就是前驅節點.
（2）right指向的是右子樹，也可能是指向后繼節點，比如 “1節點” 的right 指向的是右子樹，而 “10節點” 的right 指向的是后繼節點.

3.2. 代碼實現

package tree.threadedbinarytree;//import tree.HeroNode;public class ThreadedBinaryTreeDemo {public static void main(String[] args) {HeroNode root = new HeroNode(1, "tom");HeroNode node2 = new HeroNode(3, "jack");HeroNode node3 = new HeroNode(6, "smith");HeroNode node4 = new HeroNode(8, "mary");HeroNode node5 = new HeroNode(10, "king");HeroNode node6 = new HeroNode(14, "dim");// 二叉樹，這里手動創建方法比較低級，后面要學習遞歸創建root.setLeft(node2);root.setRight(node3);node2.setLeft(node4);node2.setRight(node5);node3.setLeft(node6);// 測試線索化ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();threadedBinaryTree.setRoot(root);threadedBinaryTree.threadedNodes();// 測試,以10節點測試HeroNode leftNode = node5.getLeft();System.out.println("10號節點的前驅節點是：" + leftNode);HeroNode rightNode = node5.getRight();System.out.println("10號節點的前驅節點是：" + rightNode);}}//
//編寫一個ArrayBinaryTree,實現順序存儲二叉樹遍歷
//定義一個ThreadedBinaryTree，實現了線索化功能的二叉樹
class ThreadedBinaryTree {private HeroNode root;// 為了實現線索化，需要創建要指向當前節點的前驅節點的指針// 在遞歸進行線索化時，pre 總是保留前一個節點private HeroNode pre = null;public void setRoot(HeroNode root) {this.root = root;}// 重載public void threadedNodes() {this.threadedNodes(root);}// 編寫對二叉樹進行中序線索化的方法/*** * @param node 就是當前需要線索化的節點*/public void threadedNodes(HeroNode node) {// 如果node==null，不能線索化if (node == null) {return;}// 1. 先線索化左子樹threadedNodes(node.getLeft());// 2. 然后線索化當前節點[有難度]// 先處理當前節點的前驅節點// 以8節點來理解// 8節點的.left=null, 8節點的.leftType=1if (node.getLeft() == null) {// 讓當前節點的左指針指向前驅節點node.setLeft(pre);// 修改當前節點的左指針的類型node.setLeftType(1);}// 處理后繼結點if (pre != null && pre.getRight() == null) {// 讓前驅節點的有指針指向當前節點pre.setRight(node);// 修改前驅節點的有指針類型pre.setRightType(1);}// !!!每處理一個節點后，讓當前節點是下一個節點的前驅節點pre = node;// 3. 再線索化右子樹threadedNodes(node.getRight());}// 刪除節點public void delNode(int no) {if (root != null) {// 如果只有一個root節點，這里立即判斷root是不是就是要刪除的節點if (root.getNo() == no) {root = null;} else {// 遞歸刪除root.delNode(no);}} else {System.out.println("空數，不能刪除~");}}// 前序遍歷public void preOrder() {if (this.root != null) {this.root.preOrder();} else {System.out.println("二叉樹為空，無法遍歷");}}// 中序遍歷public void infixOrder() {if (this.root != null) {this.root.infixOrder();} else {System.out.println("二叉樹為空，無法遍歷");}}// 后序遍歷public void postOrder() {if (this.root != null) {this.root.postOrder();} else {System.out.println("二叉樹為空，無法遍歷");}}// 前序遍歷查找public HeroNode preOrderSearch(int no) {if (root != null) {return root.preOrderSearch(no);} else {return null;}}// 中序遍歷public HeroNode infixOrderSearch(int no) {if (root != null) {return root.infixOrderSearch(no);} else {return null;}}// 后序遍歷public HeroNode postOrderSearch(int no) {if (root != null) {return this.root.postOrderSearch(no);} else {return null;}}
}//創建HeroNode
//先創建HeroNode節點
class HeroNode {private int no;private String name;private HeroNode left;// 默認nullprivate HeroNode right;// 默認null// 說明// 1. 如果leftType == 0 表示指向的是左子樹，如果1 則表示指向前驅節點// 2. 如果rightType == 0 表示指向的是右子樹，如果1 則表示指向后繼結點private int leftType;private int rightType;public int getLeftType() {return leftType;}public void setLeftType(int leftType) {this.leftType = leftType;}public int getRightType() {return rightType;}public void setRightType(int rightType) {this.rightType = rightType;}public HeroNode(int no, String name) {super();this.no = no;this.name = name;}public int getNo() {return this.no;}public void setNo(int no) {this.no = no;}public String getName() {return this.name;}public void setName(String name) {this.name = name;}public HeroNode getLeft() {return this.left;}public void setLeft(HeroNode left) {this.left = left;}public HeroNode getRight() {return this.right;}public void setRight(HeroNode right) {this.right = right;}@Overridepublic String toString() {return "HeroNode [no=" + no + ", name=" + name + "]";}// 遞歸刪除節點// 1. 如果刪除的節點是葉子節點，則刪除該節點// 2. 如果刪除的節點是非葉子節點，則刪除該子樹public void delNode(int no) {// 思路/** 1.因為我們的二叉樹是單向的，所以我們是判斷當前節點的子節點是否需要刪除結點，而不能去判斷當前這個節點是不是需要刪除節點。* 2.如果當前節點的左子節點不為空，并且左子節點就是要刪除節點，就將this.left=null，并且就返回(結束遞歸刪除)* 3.如果當前節點的右子節點不為空，并且右子節點就是要刪除節點，就將this.right=null，并且就返回(結束遞歸刪除)* 4.如果第2和第3步沒有刪除節點，那么就需要向左子樹進行遞歸刪除 5.如果第4步也沒有刪除節點，則應當向右子樹進行遞歸刪除*/// 2.如果當前節點的左子節點不為空，并且左子節點就是要刪除節點，就將this.left=null，并且就返回(結束遞歸刪除)if (this.left != null && this.left.no == no) {this.left = null;return;}// 3.如果當前節點的右子節點不為空，并且右子節點就是要刪除節點，就將this.right=null，并且就返回(結束遞歸刪除)if (this.right != null && this.right.no == no) {this.right = null;return;}// 4.如果第2和第3步沒有刪除節點，那么就需要向左子樹進行遞歸刪除if (this.left != null) {this.left.delNode(no);}// 5.如果第4步也沒有刪除節點，則應當向右子樹進行遞歸刪除if (this.right != null) {this.right.delNode(no);}}// 編寫前序遍歷的方法public void preOrder() {System.out.println(this);// 先輸出父節點// 遞歸向左子樹前序遍歷if (this.left != null) {this.left.preOrder();}// 遞歸向右子樹前序遍歷if (this.right != null) {this.right.preOrder();}}// 編寫中序遍歷的方法public void infixOrder() {// 遞歸向左子樹中序遍歷if (this.left != null) {this.left.infixOrder();}// 輸出父節點System.out.println(this);// 遞歸向右子樹中序遍歷if (this.right != null) {this.right.infixOrder();}}// 編寫后序遍歷的方法public void postOrder() {if (this.left != null) {this.left.postOrder();}if (this.right != null) {this.right.postOrder();}System.out.println(this);}// 前序遍歷查找/*** * @param no 查找的編號* @return 如果找到就返回該Node，如果沒有找到就返回null*/public HeroNode preOrderSearch(int no) {System.out.println("進入了前序查找一次~~");// 比較當前節點是不是if (this.no == no) {return this;}// 1. 判斷當前節點的左子節點是否為空，如果不為空，則遞歸前序查找// 2. 如果左遞歸前序查找，找到節點，則返回HeroNode resNode = null;if (this.left != null) {resNode = this.left.preOrderSearch(no);}if (resNode != null) {// 說明我們左子樹找到return resNode;}// 1. 左遞歸前序查找，找到節點，則返回，否繼續判斷，// 2.當前的節點的右子節點是否為空,如果不空，則繼續向右遞歸前序查找if (this.right != null) {resNode = this.right.preOrderSearch(no);}return resNode;}// 中序遍歷查找public HeroNode infixOrderSearch(int no) {// 判斷當前節點的左子節點是否為空，如果不為空，則遞歸中序查找HeroNode resNode = null;if (this.left != null) {resNode = this.left.infixOrderSearch(no);}if (resNode != null) {return resNode;}System.out.println("進入了中序查找一次~~");// 如果找到，則返回，如果沒有找到，就和當前結點比較，如果是則返回當前節點if (this.no == no) {return this;}// 否則繼續進行右遞歸的中序查找if (this.right != null) {resNode = this.right.infixOrderSearch(no);}return resNode;}// 后序遍歷查找public HeroNode postOrderSearch(int no) {// 判斷當前節點的左節點是否為空，如果不為空，則遞歸后序查找HeroNode resNode = null;if (this.left != null) {resNode = this.left.postOrderSearch(no);}if (resNode != null) {// 說明在左子樹找到return resNode;}// 如果左子樹沒有找到，則向右子樹遞歸進行后序遍歷查找if (this.right != null) {resNode = this.right.postOrderSearch(no);}if (resNode != null) {return resNode;}System.out.println("進入了后序查找一次~~");// 如果左右子樹都沒有找到，就比較當前節點是不是if (this.no == no) {return this;}return resNode;}}

運行結果：

在這里插入圖片描述

4. 遍歷線索化二叉樹

????

問題：
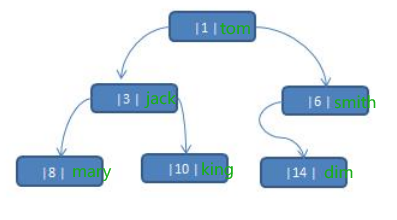
????對前面的中序線索化的二叉樹， 進行遍歷
在這里插入圖片描述

分析：
????因為線索化后，各個結點指向有變化，因此原來的遍歷方式不能使用，這時需要使用新的方式遍歷線索化二叉樹，各個節點可以通過線型方式遍歷，因此無需使用遞歸方式，這樣也提高了遍歷的效率。 遍歷的次序應當和中序遍歷保持一致。

4.1. 代碼實現

package tree.threadedbinarytree;//import tree.HeroNode;public class ThreadedBinaryTreeDemo {public static void main(String[] args) {HeroNode root = new HeroNode(1, "tom");HeroNode node2 = new HeroNode(3, "jack");HeroNode node3 = new HeroNode(6, "smith");HeroNode node4 = new HeroNode(8, "mary");HeroNode node5 = new HeroNode(10, "king");HeroNode node6 = new HeroNode(14, "dim");// 二叉樹，這里手動創建方法比較低級，后面要學習遞歸創建root.setLeft(node2);root.setRight(node3);node2.setLeft(node4);node2.setRight(node5);node3.setLeft(node6);// 測試線索化ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();threadedBinaryTree.setRoot(root);threadedBinaryTree.threadedNodes();// 測試,以10節點測試HeroNode leftNode = node5.getLeft();System.out.println("10號節點的前驅節點是：" + leftNode);HeroNode rightNode = node5.getRight();System.out.println("10號節點的前驅節點是：" + rightNode);// 當線索化二叉樹后，不能再使用原來的遍歷方法(threadedBinaryTree.infixOrder();)System.out.println("使用線索化的方式遍歷 線索化二叉樹");threadedBinaryTree.threadedList();}}//編寫一個ArrayBinaryTree,實現順序存儲二叉樹遍歷
//定義一個ThreadedBinaryTree，實現了線索化功能的二叉樹
class ThreadedBinaryTree {private HeroNode root;// 為了實現線索化，需要創建要指向當前節點的前驅節點的指針// 在遞歸進行線索化時，pre 總是保留前一個節點private HeroNode pre = null;public void setRoot(HeroNode root) {this.root = root;}// 重載public void threadedNodes() {this.threadedNodes(root);}// 遍歷線索化二叉樹的方法public void threadedList() {// 定義一個變量，存儲當前遍歷的節點，從root開始HeroNode node = root;while (node != null) {// 循環的找到leftType==1的節點，第一個找到的就是8節點// 后面隨著遍歷而變化，因為當leftType==1時，說明該節點是按照線索化處理后的有效節點while (node.getLeftType() == 0) {node = node.getLeft();}// 打印當前這個節點System.out.println(node);// 如果當前節點的右指針指向的是后繼節點，就一直輸出while (node.getRightType() == 1) {// 獲取到當前節點的后繼節點node = node.getRight();System.out.println(node);}// 替換遍歷的節點node = node.getRight();}}// 編寫對二叉樹進行中序線索化的方法/*** * @param node 就是當前需要線索化的節點*/public void threadedNodes(HeroNode node) {// 如果node==null，不能線索化if (node == null) {return;}// 1. 先線索化左子樹threadedNodes(node.getLeft());// 2. 然后線索化當前節點[有難度]// 先處理當前節點的前驅節點// 以8節點來理解// 8節點的.left=null, 8節點的.leftType=1if (node.getLeft() == null) {// 讓當前節點的左指針指向前驅節點node.setLeft(pre);// 修改當前節點的左指針的類型node.setLeftType(1);}// 處理后繼結點if (pre != null && pre.getRight() == null) {// 讓前驅節點的有指針指向當前節點pre.setRight(node);// 修改前驅節點的有指針類型pre.setRightType(1);}// !!!每處理一個節點后，讓當前節點是下一個節點的前驅節點pre = node;// 3. 再線索化右子樹threadedNodes(node.getRight());}// 刪除節點public void delNode(int no) {if (root != null) {// 如果只有一個root節點，這里立即判斷root是不是就是要刪除的節點if (root.getNo() == no) {root = null;} else {// 遞歸刪除root.delNode(no);}} else {System.out.println("空數，不能刪除~");}}// 前序遍歷public void preOrder() {if (this.root != null) {this.root.preOrder();} else {System.out.println("二叉樹為空，無法遍歷");}}// 中序遍歷public void infixOrder() {if (this.root != null) {this.root.infixOrder();} else {System.out.println("二叉樹為空，無法遍歷");}}// 后序遍歷public void postOrder() {if (this.root != null) {this.root.postOrder();} else {System.out.println("二叉樹為空，無法遍歷");}}// 前序遍歷查找public HeroNode preOrderSearch(int no) {if (root != null) {return root.preOrderSearch(no);} else {return null;}}// 中序遍歷public HeroNode infixOrderSearch(int no) {if (root != null) {return root.infixOrderSearch(no);} else {return null;}}// 后序遍歷public HeroNode postOrderSearch(int no) {if (root != null) {return this.root.postOrderSearch(no);} else {return null;}}
}//創建HeroNode
//先創建HeroNode節點
class HeroNode {private int no;private String name;private HeroNode left;// 默認nullprivate HeroNode right;// 默認null// 說明// 1. 如果leftType == 0 表示指向的是左子樹，如果1 則表示指向前驅節點// 2. 如果rightType == 0 表示指向的是右子樹，如果1 則表示指向后繼結點private int leftType;private int rightType;public int getLeftType() {return leftType;}public void setLeftType(int leftType) {this.leftType = leftType;}public int getRightType() {return rightType;}public void setRightType(int rightType) {this.rightType = rightType;}public HeroNode(int no, String name) {super();this.no = no;this.name = name;}public int getNo() {return this.no;}public void setNo(int no) {this.no = no;}public String getName() {return this.name;}public void setName(String name) {this.name = name;}public HeroNode getLeft() {return this.left;}public void setLeft(HeroNode left) {this.left = left;}public HeroNode getRight() {return this.right;}public void setRight(HeroNode right) {this.right = right;}@Overridepublic String toString() {return "HeroNode [no=" + no + ", name=" + name + "]";}// 遞歸刪除節點// 1. 如果刪除的節點是葉子節點，則刪除該節點// 2. 如果刪除的節點是非葉子節點，則刪除該子樹public void delNode(int no) {// 思路/** 1.因為我們的二叉樹是單向的，所以我們是判斷當前節點的子節點是否需要刪除結點，而不能去判斷當前這個節點是不是需要刪除節點。* 2.如果當前節點的左子節點不為空，并且左子節點就是要刪除節點，就將this.left=null，并且就返回(結束遞歸刪除)* 3.如果當前節點的右子節點不為空，并且右子節點就是要刪除節點，就將this.right=null，并且就返回(結束遞歸刪除)* 4.如果第2和第3步沒有刪除節點，那么就需要向左子樹進行遞歸刪除 5.如果第4步也沒有刪除節點，則應當向右子樹進行遞歸刪除*/// 2.如果當前節點的左子節點不為空，并且左子節點就是要刪除節點，就將this.left=null，并且就返回(結束遞歸刪除)if (this.left != null && this.left.no == no) {this.left = null;return;}// 3.如果當前節點的右子節點不為空，并且右子節點就是要刪除節點，就將this.right=null，并且就返回(結束遞歸刪除)if (this.right != null && this.right.no == no) {this.right = null;return;}// 4.如果第2和第3步沒有刪除節點，那么就需要向左子樹進行遞歸刪除if (this.left != null) {this.left.delNode(no);}// 5.如果第4步也沒有刪除節點，則應當向右子樹進行遞歸刪除if (this.right != null) {this.right.delNode(no);}}// 編寫前序遍歷的方法public void preOrder() {System.out.println(this);// 先輸出父節點// 遞歸向左子樹前序遍歷if (this.left != null) {this.left.preOrder();}// 遞歸向右子樹前序遍歷if (this.right != null) {this.right.preOrder();}}// 編寫中序遍歷的方法public void infixOrder() {// 遞歸向左子樹中序遍歷if (this.left != null) {this.left.infixOrder();}// 輸出父節點System.out.println(this);// 遞歸向右子樹中序遍歷if (this.right != null) {this.right.infixOrder();}}// 編寫后序遍歷的方法public void postOrder() {if (this.left != null) {this.left.postOrder();}if (this.right != null) {this.right.postOrder();}System.out.println(this);}// 前序遍歷查找/*** * @param no 查找的編號* @return 如果找到就返回該Node，如果沒有找到就返回null*/public HeroNode preOrderSearch(int no) {System.out.println("進入了前序查找一次~~");// 比較當前節點是不是if (this.no == no) {return this;}// 1. 判斷當前節點的左子節點是否為空，如果不為空，則遞歸前序查找// 2. 如果左遞歸前序查找，找到節點，則返回HeroNode resNode = null;if (this.left != null) {resNode = this.left.preOrderSearch(no);}if (resNode != null) {// 說明我們左子樹找到return resNode;}// 1. 左遞歸前序查找，找到節點，則返回，否繼續判斷，// 2.當前的節點的右子節點是否為空,如果不空，則繼續向右遞歸前序查找if (this.right != null) {resNode = this.right.preOrderSearch(no);}return resNode;}// 中序遍歷查找public HeroNode infixOrderSearch(int no) {// 判斷當前節點的左子節點是否為空，如果不為空，則遞歸中序查找HeroNode resNode = null;if (this.left != null) {resNode = this.left.infixOrderSearch(no);}if (resNode != null) {return resNode;}System.out.println("進入了中序查找一次~~");// 如果找到，則返回，如果沒有找到，就和當前結點比較，如果是則返回當前節點if (this.no == no) {return this;}// 否則繼續進行右遞歸的中序查找if (this.right != null) {resNode = this.right.infixOrderSearch(no);}return resNode;}// 后序遍歷查找public HeroNode postOrderSearch(int no) {// 判斷當前節點的左節點是否為空，如果不為空，則遞歸后序查找HeroNode resNode = null;if (this.left != null) {resNode = this.left.postOrderSearch(no);}if (resNode != null) {// 說明在左子樹找到return resNode;}// 如果左子樹沒有找到，則向右子樹遞歸進行后序遍歷查找if (this.right != null) {resNode = this.right.postOrderSearch(no);}if (resNode != null) {return resNode;}System.out.println("進入了后序查找一次~~");// 如果左右子樹都沒有找到，就比較當前節點是不是if (this.no == no) {return this;}return resNode;}}

運行結果：

在這里插入圖片描述

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/210504.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/210504.shtml
英文地址，請注明出處：http://en.pswp.cn/news/210504.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

1688API接口系列，商品詳情數據丨搜索商品列表丨商家訂單類丨1688開放平臺接口使用方案

1688API接口系列，商品詳情數據丨搜索商品列表丨商家訂單類丨1688開放平臺接口使用方案

1688商品詳情接口是指1688平臺提供的API接口，用于獲取商品詳情信息。通過該接口，您可以獲取到商品的詳細信息，包括商品標題、價格、庫存、描述、圖片等。 要使用1688商品詳情接口，您需要先申請1688的API權限，并獲取ac…
閱讀更多...
老有所依：TSINGSEE青犀養老院智能視頻監管方案

老有所依：TSINGSEE青犀養老院智能視頻監管方案

養老院智能監控方案是為了提高養老院內老人的安全和護理質量，利用智能技術與監控設備進行全方位的監控和管理，可以加強對老人的監護和護理，提高養老院的服務質量和安全性。 旭帆科技基于視頻技術與AI智能分析技術構建的養老院智能視頻監控方…
閱讀更多...
[動態規劃]最長公共子序列

[動態規劃]最長公共子序列

題目六 最長公共子序列 題目描述 我們稱一個字符的數組S為一個序列。對于另外一個字符數組Z,如果滿足以下條件，則稱Z是S的一個子序列：（1）Z中的每個元素都是S中的元素（2）Z中元素的順序與在S中的順序一致。…
閱讀更多...
22 FlexSPI—讀寫外部 SPI NorFlash

22 FlexSPI—讀寫外部 SPI NorFlash

文章目錄 22.1 SPI 協議簡介22.1.1 SPI物理層22.1.2 協議22.1.3 CPOL/CPHA 及通訊模式22.1.4 擴展 SPI 協議22.1.5 SDR 和 DDR 模式 22.2 RT1052 的 FlexSPI 特性及架構22.2.1 RT1052 的 FlexSPI 外設簡介22.2.2 RT1052 的 FlexSPI 架構剖析22.2.2.1 通訊引腳22.2.2.2 指令查找…
閱讀更多...
如何將html網頁免費轉為excel？

如何將html網頁免費轉為excel？

一、直接復制。 直接復制是最簡單有效、快捷的解決方案，操作方法如下： 1、用鼠標像平常復制文本一樣，將整個網頁表格選中。 2、點擊右鍵，點擊“復制”。 3、打開excel軟件，鼠標點擊任意單元格。 4、點擊右鍵&#…
閱讀更多...
Power BI - 5分鐘學習拆分列

Power BI - 5分鐘學習拆分列

每天5分鐘，今天介紹Power BI拆分列功能。 什么是拆分列？ 有時導入Power BI的數據表中，某列內容都包含同樣的特殊字符如 /&/-/_等，可以利用這個特殊字符進行拆分列的操作，獲得我們想要的信息。 操作舉例&#xf…
閱讀更多...
【從編譯器的角度看多態的底層實現原理】

【從編譯器的角度看多態的底層實現原理】

系列文章目錄 歡迎讀者訂閱《計算機底層原理》、《從JVM看Java》系列文章、能夠幫助到大家就是對我最大的鼓勵！ 文章目錄 目錄 系列文章目錄 文章目錄 前言 一、編譯器做了什么？ 1.詞法分析 2.語法分析 3.語義分析 4.中間代碼生成 5.優化 6.目標代碼生成…
閱讀更多...
SugarCRM 任意文件上傳漏洞復現(CVE-2023-22952)

SugarCRM 任意文件上傳漏洞復現(CVE-2023-22952)

0x01 產品簡介 SugarCRM是美國SugarCRM公司的一套開源的客戶關系管理系統（CRM）。該系統支持對不同的客戶需求進行差異化營銷、管理和分配銷售線索，實現銷售代表的信息共享和追蹤。 0x02 漏洞概述 SugarCRM index.php接口存在安全漏洞，該漏洞源于安裝組件中存在授權繞過和P…
閱讀更多...
在線人數（oj題）

在線人數（oj題）

題目不少于5個字，所以整了個括號湊字數 首先我想到的是用一個數組來記錄每一秒的在線人數 但是即使是short類型（2字節），也會用到60 * 60 * 24 * 30 * 12 * 60 * 2 / 1024 / 1024 3,559.5703125 MB 而題目上限是256MB&#xff0…
閱讀更多...
UE小：UE5性能分析

UE小：UE5性能分析

開始錄制性能追蹤 要開始錄制性能追蹤，您可以簡單地點擊界面上的“開始錄制”按鈕。 查看追蹤數據 錄制完成后，點擊“Trace”菜單中的“UnrealInsights”選項來查看追蹤數據。 使用命令行進行追蹤 如果點擊錄制按鈕沒有反應，您可以通過命令…
閱讀更多...
【頭歌系統數據庫實驗】實驗4 MySQL單表查詢

【頭歌系統數據庫實驗】實驗4 MySQL單表查詢

目錄 第1關. 在users表中新增一個用戶，user_id為2019100904學號，name為2019-物聯網-李明 第2關. 在users表中更新用戶 user_id為robot_2 的信息，name設為 機器人二號 第3關. 將solution表中所有 problem_id 為1003 題目的解答結果&#xf…
閱讀更多...
python源碼，在線讀取傳奇列表，并解析為需要的JSON格式

python源碼，在線讀取傳奇列表，并解析為需要的JSON格式

python源碼，在線讀取傳奇列表，并解析為需要的JSON格式 [Server] ; 使用“/”字符分開顏色，也可以不使用顏色，支持以前的舊格式，只有標題和服務器標題支持顏色 ; 標題/顏色代碼(0-255)|服務器標題/顏色代碼(0-255)|服務…
閱讀更多...
使用醫學數據集MIMIC，常見的問題記錄

使用醫學數據集MIMIC，常見的問題記錄

目錄 MIMIC數據庫安裝及數據導入教程1.postgresql安裝第一步：error running考慮到是不是不同的sql的沖突從報錯信息出發重啟之后可以安裝了 2.打開navicate153.7z 不是內部或外部命令，也不是可運行的程序4.在postgreSQL中輸入**\i xxx**命令后遇到提示pe…
閱讀更多...
2023年9月26日 Go生態洞察：深入解析類型參數

2023年9月26日 Go生態洞察：深入解析類型參數

🌷🍁 博主貓頭虎（🐅🐾）帶您 Go to New World?🍁 🦄 博客首頁——🐅🐾貓頭虎的博客🎐 🐳 《面試題大全專欄》 🦕 文章圖文…
閱讀更多...
2023第十二屆“認證杯”D題：CMOS黃昏系數|數學中國數學建模國際賽（小美賽）| 建模秘籍文章代碼思路大全

2023第十二屆“認證杯”D題：CMOS黃昏系數|數學中國數學建模國際賽（小美賽）| 建模秘籍文章代碼思路大全

鐺鐺！小秘籍來咯！ 小秘籍希望大家都能輕松建模呀，數維杯也會持續給大家放送思路滴~ 抓緊小秘籍，我們出發吧~ 來看看認證杯（D題）！ 完整內容可以在文章末尾領取！ 問題重述&#x…
閱讀更多...
【小紅書運營指南1】賽道選擇 + 賬號運營全周期

【小紅書運營指南1】賽道選擇 + 賬號運營全周期

小紅書運營指南1 寫在最前面11.23標簽一級標簽二級標簽 網絡資源整理1. 賽道選擇近2年小紅書女性人群畫像 2. 基礎認知階段3. 賬號啟動階段4. 選題規劃階段5. 爆款打造階段6. 漲粉變現階段漲粉變現階段粉絲發展階段 寫在最前面 最近做的一個項目調研，調研和實際有一…
閱讀更多...
每日移到算法題 1

每日移到算法題 1

借鑒文章：Java-敏感字段加密 - 嗶哩嗶哩 題目描述 給定一個由多個命令字組成的命令字符串； 1、字符串長度小于等于127字節，只包含大小寫字母，數字，下劃線和偶數個雙引號 2、命令字之間以一個或多個下劃線_進行分割…
閱讀更多...
設計模式-工廠模式(Factory)

設計模式-工廠模式(Factory)

Factory模式是一種創建型設計模式&#xff0c;用于封裝對象的實例化過程。它提供了一個統一的接口來創建不同類型的對象&#xff0c;而無需暴露具體的實例化邏輯給客戶端。 #include <iostream> #include <memory>// AbstractProduct&#xff08;抽象產品類&#…
閱讀更多...
mybatis-plus處理blob字段

mybatis-plus處理blob字段

轉載自&#xff1a;www.javaman.cn 在 Spring Boot 項目中使用 MyBatis-Plus 處理 longblob 字段時&#xff0c;我們可以按照以下步驟進行操作。假設 longblob 存儲的是字符串數據。以下是完整的示例代碼&#xff1a; 添加依賴&#xff1a;在你的項目的 pom.xml 文件中添加 My…
閱讀更多...
js判斷上傳的文件是GBK編碼還是UTF-8

js判斷上傳的文件是GBK編碼還是UTF-8

1、獲取文件二進制數據&#xff0c;這里只做示例&#xff0c;例如element-ui中文件上傳的beforeUpload方法&#xff0c;返回的file對象&#xff0c;然后使用FileReader對其進行轉換&#xff0c;再進行后續判斷 function beforeUpload(file: File) { const reader new FileRea…
閱讀更多...
最新文章

Copyright @ 2022~2023