1.引入

2.概念

3.解決方法

4.例題

5.回顧

1.引入

經典的七橋問題

哥尼斯堡是位于普累格河上的一座城市，它包含兩個島嶼及連接它們的七座橋，如下圖所示。

可否走過這樣的七座橋，而且每橋只走過一次？

你怎樣證明？

后來大數學家歐拉把它轉化成一個幾何問題——一筆畫問題。

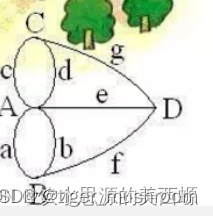
我們的大數學家歐拉，找到了它的重要條件

1.奇點的數目不是0個就是2個

奇點：就是度為奇數（有向圖是判斷出度與入度是否相等），反之為偶點

有向圖1、連通 2、所有點出度等于入度或者一個點入度-出度=1，另外一個點出度-入度=1

2.圖是聯通的

2.概念

歐拉路：對于一個圖，每條邊可以且只能訪問一次

歐拉回路：在歐拉圖的情況下，最后要回到原點。也就是說歐拉路不一定是歐拉回路，但歐拉回路一定是歐拉路

3.解決方法：
1.dfs

第一步：判斷圖是否連通

第二步：判斷奇點個數

很簡單，但是使用dfs的話，就需要很多數組，并且用鄰接矩陣是最方便的，所以費空間

2.并查集

分為G1和G2兩個集合，G1表示已經聯通的，G2表示未聯通的

利用父親表示法合并集合效率最高，也是上面那兩步

4.例題

（1）

一筆畫問題

題目描述

如果一個無向圖存在一筆畫，則一筆畫的路徑叫做歐拉路，如果最后又回到起點，那這個路徑叫做歐拉回路。

輸入

第一行n，m，0 < n <=20，表示有n個點，m條邊，以下m行描述每條邊連接的兩點。

輸出

如果有歐拉路或歐拉回路，輸出一條路徑即可，頂點之間由空格隔開。

如果沒有，輸出NO
?

樣例輸入1

5?5
1?2
2?3
3?4
4?5
5?1

樣例輸出1

1?5?4?3?2?1

解法

1.dfs

簡單，實用

費空間費時間

2.并查集

效率高，快速，不費時間不費空間

難，費勁

本蒟蒻用的是DFS

1、判斷連通性，沒有判斷
就是要判斷所有點都是連通的（dfs或者并查集）
如果不連通輸出NO

2、如果連通，統計奇點的個數
如果奇點個數為0則為歐拉回路
如果奇點個數為2則為歐拉路
其他情況則輸出NO

3、輸出一個路徑

dfs:

void dfs(int i)
{for(int j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++reckon]=i;return;
}

調題過程很坎坷

40分：（未判斷NO)

#include<bits/stdc++.h>
using namespace std;
#define N 510
int g[N][N],d[N],c[N],n,m,p;
int dfs(int i)
{int j;for(j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++p]=i;return 0;
}int main()
{cin>>n>>m;int x,y;memset(g,0,sizeof(g));for(int i=1;i<=m;i++){cin>>x>>y;g[x][y]=1;g[y][x]=1;d[x]++;d[y]++;}int z=1;for(int i=1;i<=n;i++){if(d[i]%2==1){z=i;}}dfs(z);for(int i=1;i<=p;i++){cout<<c[i]<<" ";}return 0;
}//40分

60分：（未判斷連通性）

#include<bits/stdc++.h>
using namespace std;
#define N 510
int g[N][N],d[N],c[N],n,m,reckon,oddity_point;
void dfs(int i)
{for(int j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++reckon]=i;return;
}int main()
{cin>>n>>m;int x,y;memset(g,0,sizeof(g));for(int i=1;i<=m;i++){cin>>x>>y;g[x][y]=1;g[y][x]=1;d[x]++;d[y]++;}int z=1;for(int i=1;i<=n;i++){if(d[i]%2==1){z=i;oddity_point++;}}dfs(z);if(oddity_point!=2&&oddity_point!=0){cout<<"NO";return 0;}for(int i=1;i<=reckon;i++){cout<<c[i]<<" ";}return 0;
}//60分

100分AC：

#include<bits/stdc++.h>
using namespace std;
#define N 510
int g[N][N],d[N],c[N],n,m,reckon,oddity_point,lt;
void dfs(int i)
{for(int j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++reckon]=i;return;
}int main()
{cin>>n>>m;int x,y;memset(g,0,sizeof(g));for(int i=1;i<=m;i++){cin>>x>>y;g[x][y]=1;g[y][x]=1;d[x]++;d[y]++;}int z=1;for(int i=1;i<=n;i++){if(d[i]%2==1){z=i;oddity_point++;}if(d[i]==0){lt++;}}dfs(z);if(oddity_point!=2&&oddity_point!=0){cout<<"NO";return 0;}if(lt!=0){cout<<"NO";return 0;}for(int i=1;i<=reckon;i++){cout<<c[i]<<" ";}return 0;
}//AC

5.回顧

因為我的測試點沒有測出來問題所在：

問題：

如果1-2-3-4四個點一個環，5-6兩個點連通，奇點個數為2，但整個圖不連通

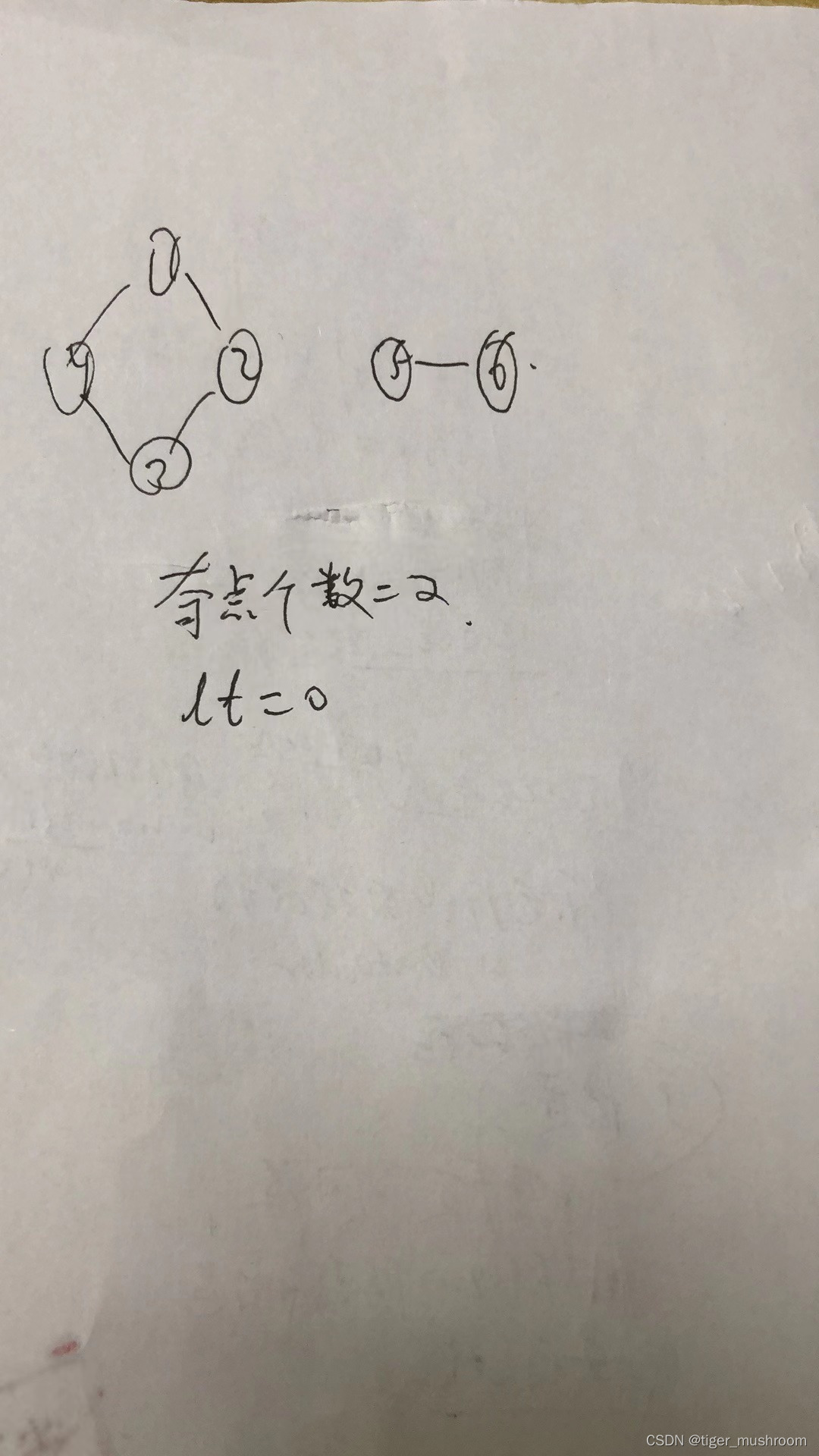
我的程序會說YES

可是根本不連通

輸出5 6

碰上這樣的就必須用DFS，并查集了

本蒟蒻偷了個小懶

因為碰上這樣的（錯誤）輸出一定不會是m+1個

所以判斷一下輸出個數是不是不等于m+1

如果不等于，輸出NO。

#include<bits/stdc++.h>
using namespace std;
#define N 510
int g[N][N],d[N],c[N],n,m,reckon,oddity_point,lt;
void dfs(int i)
{for(int j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++reckon]=i;return;
}
int main()
{cin>>n>>m;int x,y;memset(g,0,sizeof(g));for(int i=1;i<=m;i++){cin>>x>>y;g[x][y]=1;g[y][x]=1;d[x]++;d[y]++;}int z=1;for(int i=1;i<=n;i++){if(d[i]%2==1){z=i;oddity_point++;}if(d[i]==0){lt++;}}dfs(z);if(oddity_point!=2&&oddity_point!=0){cout<<"NO";return 0;}if(lt!=0){cout<<"NO";return 0;}if(reckon!=m+1){cout<<"NO";return 0;}for(int i=1;i<=reckon;i++){cout<<c[i]<<" ";}return 0;
}

最終，我們把無用的代碼段刪掉，調試結束

#include<bits/stdc++.h>
using namespace std;
#define N 510
int g[N][N],d[N],c[N],n,m,reckon,oddity_point,lt;
void dfs(int i)
{for(int j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++reckon]=i;return;
}
int main()
{cin>>n>>m;int x,y;memset(g,0,sizeof(g));for(int i=1;i<=m;i++){cin>>x>>y;g[x][y]=1;g[y][x]=1;d[x]++;d[y]++;}int z=1;for(int i=1;i<=n;i++){if(d[i]%2==1){z=i;oddity_point++;}}dfs(z);//判斷連通性if(reckon!=m+1){cout<<"NO";return 0;}//判斷奇點個數if(oddity_point!=2&&oddity_point!=0){cout<<"NO";return 0;}for(int i=1;i<=reckon;i++){cout<<c[i]<<" ";}return 0;
}