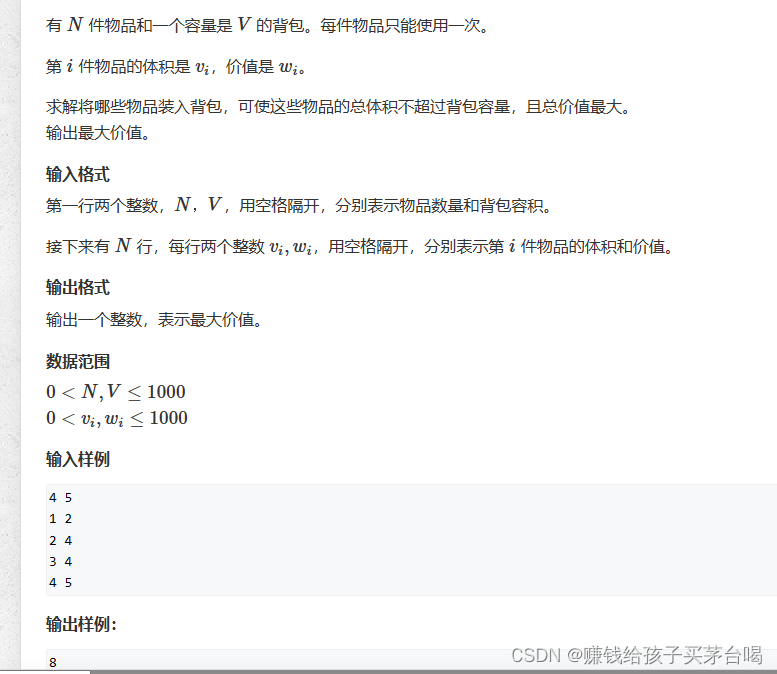
二維版:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;public class Main {static int N = 1010;static int[][] dp = new int[N][N]; //dp[i][j] 只選前i件物品,體積 <= j的最優解static int[] w = new int[N]; //存儲價值static int[] v = new int[N]; //存儲體積static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));public static void main(String[] args) throws IOException{String[] init = in.readLine().split(" ");int n = Integer.parseInt(init[0]);int Vmax = Integer.parseInt(init[1]);for(int i = 1;i <= n;i ++) {init = in.readLine().split(" ");v[i] = Integer.parseInt(init[0]);w[i] = Integer.parseInt(init[1]);}for(int i = 1;i <= n;i ++) {for(int j = 1;j <= Vmax;j ++) {if (v[i] > j) { //當前背包裝不下.最優解就是上一層的數據dp[i][j] = dp[i - 1][j];} else {//裝得下的話,背包的價值會變成dp[i - 1][j - v[i]] + w[i]// j - v[i] 體積下的最優解 + w[i] 不一定會勝過dp[i - 1][j]dp[i][j] = Math.max(dp[i-1][j], dp[i - 1][j - v[i]] + w[i]);}}}System.out.print(dp[n][Vmax]);in.close();}
}f[i][j]:只從前i個物品全,總體積<=j的最優解。局部最優=>全局最優

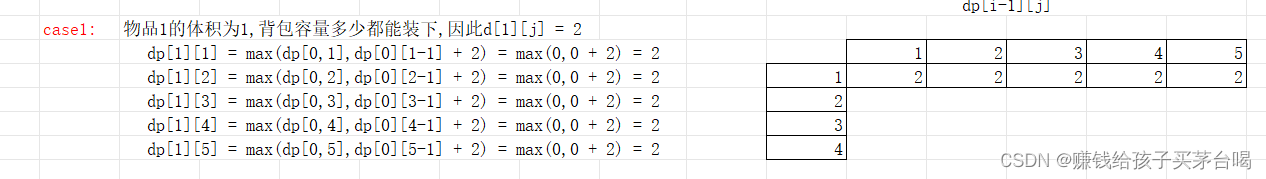



一維版
由模擬二維的過程可知,通過不斷覆蓋前一維的狀態,只一維數組也能實現
并且,并不是一維里的所有數據都需要更新,所以可以更新二維起始下標
二維更改一維需要滿足條件,在決策dp[i][j]時,要能夠知道dp[i - 1][j - v[i]]的狀態
要用的是一行的數據,不能用當前行的數據
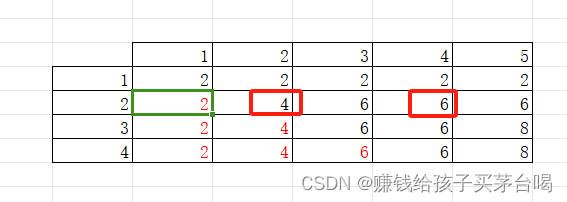
如表格中在決策第二件物品(v=2)時,dp[2]計算時,會把2更新成4,dp[4]計算時,需要用到上一次的2,而不是被更新過的4。所以決策時,每次都要用到前面的數據,但前面的數據又不能被改過。所以可以從后往前,可以確保你要決策的數,只被決策一次。
?
import java.io.*;
public class Main
{static int N = 1010;static int V;static int n;static int[] f = new int[N]; //只選前i件物品,背包容量為j的最優解static int[] v = new int[N]; //存體積static int[] w = new int[N]; //存價值static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));public static void main(String[] args)throws IOException{String[] init = in.readLine().split(" ");n = Integer.parseInt(init[0]);V = Integer.parseInt(init[1]);for(int i = 1;i <= n;i++){String[] data = in.readLine().split(" "); v[i] = Integer.parseInt(data[0]);w[i] = Integer.parseInt(data[1]);}for(int i = 1;i <= n;i++){ //從后往前決策, j < v[i] 的地方不需要更新,直接用上一次的數據for(int j = V;j >= v[i];j--){f[j] = Math.max(f[j],f[j-v[i]]+w[i]);}}System.out.println(f[V]);in.close();}
}?
?
?





)













