今天我們來看看常用的算法，開干。。。。。

算法

二叉樹左右變換數據

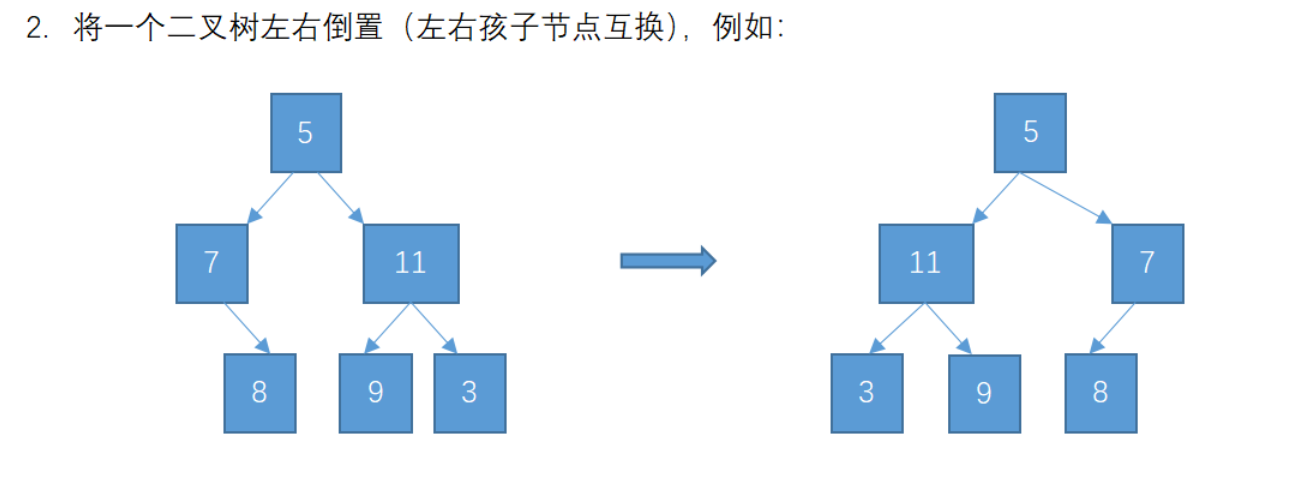
實現的代碼如下：以下定義的類是內部類

//    2. 講一個做二叉樹左右替換
//    1. 先給一個二叉樹的內部類，類里面分出左右的對象的變量public static class Tree {private Object data;public Object getData() {return data;}public void setData(Object data) {this.data = data;}public Tree getLeft() {return left;}public void setLeft(Tree left) {this.left = left;}public Tree getRight() {return right;}public void setRight(Tree right) {this.right = right;}// 給出左右的樹private Tree left;private Tree right;// 構造方法public Tree(Object data, Tree left, Tree right) {this.data = data;this.left = left;this.right = right;}/*** 獲取二叉樹的深度* @param root root* @return int*/public static int getMaxDepth(Tree root) {if (root == null) return 0;// 需要遞歸獲取深度return Math.max(getMaxDepth(root.left), getMaxDepth(root.right)) + 1;}/*** 二叉樹的交換方法OK，經過驗證* @param root Tree*/public static void swap(Tree root) {if (root == null) return;// 交換Tree tmp = root.left;root.left = root.right;root.right = tmp;// 遞歸交換swap(root.left);swap(root.right);}/***  二叉樹的左右交換* @param root*/public static void swapAgin(Tree root) {if (root == null) return;Stack<Tree> statck = new Stack<>();statck.push(root);while (!statck.isEmpty()) {Tree node = statck.pop();Tree tmp = node.left;node.left = node.right;node.right = tmp;if (node.left != null) {statck.push(node.left);}if (node.right != null) {statck.push(node.right);}}}public static void main(String[] args) {// 以下模擬的二叉樹圖片地址在此： https://img-blog.csdnimg.cn/1ae454d94ab04d8e8fb6f313248beb3a.pngTree left9 = new Tree(9, null, null);Tree right3 = new Tree(3, null, null);Tree right8 = new Tree(8, null, null);Tree left7 = new Tree(7, null, right8);Tree right11 = new Tree(11, left9, right3);Tree root5 = new Tree(5, left7, right11);System.out.println("原始的二叉樹結果：" + root5);
//       交換swap(root5);
//            swapAgin(root5);System.out.println("swap()方法交換之后的二叉樹結構為：" + root5);}}

二分法

概念：

• 二分法（Bisection method） 即一分為二的方法，又叫折半查找方法。
• 把一組有序數列分為左右兩部分，從這組數字的中間位置開始找：
• 如果中間位置的數等于目標數，則直接返回；
• 如果中間位置的數大于目標數，則從左邊部分查找；
• 如果小于目標數，則從右邊部分查找；
• 重復以上過程，直到找到滿足條件的記錄，使查找成功。

時間復雜度：
都是 O(log2 N)

空間復雜度：
非遞歸方式： 空間復雜度是O(1);
遞歸方式： 空間復雜度：O(log2N )

實現

1. 遞歸方式

 public static int binarySearchRecursive(int[] arr, int low, int high, int key) {//邊界條件：如果目標數沒有在數組范圍內（即比最左邊的數小，比最右邊的數大）if (arr == null || arr.length == 0 || arr[low] > key || arr[high] < key || low > high) {return -1;}// 獲取中間位置下標int mid = (low + high) / 2;// 將中間位置的數和目標數作比較，如果中間位置的數等于目標數，則直接返回下標，// 如果中間位置的數大于目標數，則將左邊部分用遞歸方法繼續查找；如果小于目標數，則從右邊部分用遞歸方法繼續查找if (arr[mid] == key) {return mid;} else if (arr[mid] > key) {return binarySearch(arr, low, mid - 1, key);} else {return binarySearch(arr, mid + 1, high, key);}}// 測試下：從一組數中找3，輸出數組下標public static void main(String[] args) {int[] arr = {2, 3, 5, 7, 9, 78, 90, 167};System.out.println(binarySearchRecursive(arr, 0, (arr.length) - 1, 3));}

2. 非遞歸方式

 public static int binarySearch(int[] arr, int key) {int low = 0;int high = arr.length - 1;while (low <= high) {int middle = (low + high) / 2;if (key < arr[middle]) {high = middle - 1;} else if (key > arr[middle]) {low = middle + 1;} else {return middle;}}return -1;}// 測試下：從一組數中找3，輸出數組下標public static void main(String[] args) {int[] arr = {2, 3, 5, 7, 9, 78, 90, 167};System.out.println("數組下標："+binarySearch(arr, 3));}

3.非遞歸

/*** 二分查找* @param srcArray 源數組* @param des 目標元素* @return 如果找到則返回索引位置，找不到則返回-1*/
public static int binarySearch(int[] srcArray, int des) {//定義初始最小、最大索引int start = 0;int end = srcArray.length - 1;//確保不會出現重復查找，越界while (start <= end) {//計算出中間索引值  >>> 邏輯右移 也就是 int middle = (end + start)/2int middle = (end + start)>>>1 ;//防止溢出if (des == srcArray[middle]) {return middle;//判斷下限} else if (des < srcArray[middle]) {end = middle - 1;//判斷上限} else {start = middle + 1;}}//若沒有，則返回-1return -1;
}

冒泡排序算法

算法原理：
比較相鄰的元素。如果第一個比第二個大，就交換他們兩個。
對每一對相鄰元素做同樣的工作，從開始第一對到結尾的最后一對。在這一點，最后的元素應該會是最大的數。
針對所有的元素重復以上的步驟，除了最后一個。
持續每次對越來越少的元素重復上面的步驟，直到沒有任何一對數字需要比較。

示例代碼：

public static void bubbleSort(int arr[]) {for (int i = 0; i < arr.length - 1; i++) {for (int j = 0; j < arr.length - 1 - i; j++) {if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}

示例代碼2：

public static void bubbleSort2(int[] a, int n) {int i, j;for (i = 0; i < n; i++) {//表示 n 次排序過程。for (j = 1; j < n - i; j++) {if (a[j - 1] > a[j]) {//前面的數字大于后面的數字就交換//交換 a[j-1]和 a[j]int temp;temp = a[j - 1];a[j - 1] = a[j];a[j] = temp;}}}
}

插入排序算法

（1）概念：通過構建有序序列，對于未排序數據，在已排序序列中從后向前掃描，找到相應的位置并插入。

（2）一個通俗的比喻：

插入排序就類似于斗地主時，整理撲克牌的情況。第一次摸牌時，左收是空的，之后每次摸牌插入到左手的牌時，都會將這張牌和左手中已經排好序的牌，從右到左比較，確認這張牌該放的位置。

示例代碼：

public static void insertionSort(int arr[]) {for (int i = 1; i < arr.length; i++) {//插入的數int insertVal = arr[i];//被插入的位置(準備和前一個數比較)int index = i - 1;//如果插入的數比被插入的數小while (index >= 0 && insertVal < arr[index]) {//將把 arr[index] 向后移動arr[index + 1] = arr[index];//讓 index 向前移動index--;}//把插入的數放入合適位置arr[index + 1] = insertVal;}
}

快速排序算法

（1）概念：快速排序是指通過一趟排序將要排序的數據分割成獨立的兩部分，其中一部分的所有數據都比另外一部分的所有數據都要小，然后再按此方法對這兩部分數據分別進行快速排序。整個排序過程可以遞歸進行，以此達到整個數據變成有序序列。

（2）快速排序的的過程簡圖：

選擇一個關鍵值作為基準值。比基準值小的都在左邊序列（一般是無序的），比基準值大的都在右邊（一般是無序的）。

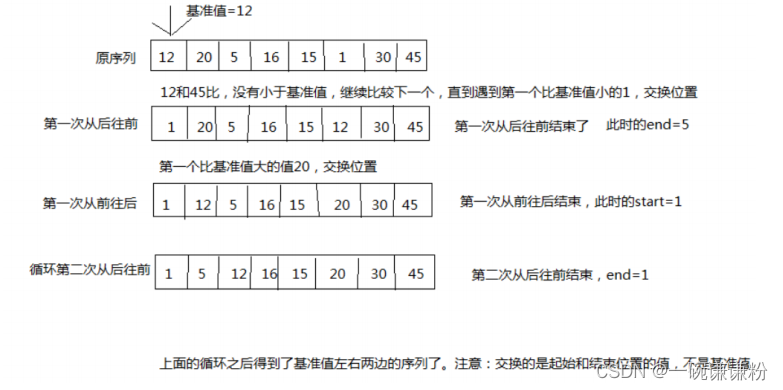
示例代碼：

/*** 快速排序** @param arr   需要排序的數組* @param start 數組的最小索引： 0* @param end   數組的最大索引： arr.length - 1* @return 排序好的數組*/
public static int[] quickSort(int arr[], int start, int end) {int pivot = arr[start];int i = start;int j = end;while (i < j) {while ((i < j) && (arr[j] > pivot)) {j--;}while ((i < j) && (arr[i] < pivot)) {i++;}if ((arr[i] == arr[j]) && (i < j)) {i++;} else {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}if (i - 1 > start) arr = quickSort(arr, start, i - 1);if (j + 1 < end) arr = quickSort(arr, j + 1, end);return (arr);
}

示例代碼2：

/*** 快速排序（無返回值）* @param a 需要排序的數組* @param low 數組的最小索引： 0* @param high 數組的最大索引： arr.length - 1*/
public static void quickSort2(int[] a, int low, int high) {int start = low;int end = high;int key = a[low];while (end > start) {//從后往前比較while (end > start && a[end] >= key)//如果沒有比關鍵值小的，比較下一個，直到有比關鍵值小的交換位置，然后又從前往后比較end--;if (a[end] <= key) {int temp = a[end];a[end] = a[start];a[start] = temp;}//從前往后比較while (end > start && a[start] <= key)//如果沒有比關鍵值大的，比較下一個，直到有比關鍵值大的交換位置start++;if (a[start] >= key) {int temp = a[start];a[start] = a[end];a[end] = temp;}//此時第一次循環比較結束，關鍵值的位置已經確定了。左邊的值都比關鍵值小，右邊的值都比關鍵值大，但是兩邊的順序還有可能是不一樣的，進行下面的遞歸調用}//遞歸if (start > low) quickSort2(a, low, start - 1);//左邊序列。第一個索引位置到關鍵值索引-1if (end < high) quickSort2(a, end + 1, high);//右邊序列。從關鍵值索引+1 到最后一個
}

希爾排序算法

（1）基本思想：先將整個待排序的記錄序列分割成為若干子序列分別進行直接插入排序，待整個序列中的記錄“基本有序”時，再對全體記錄進行依次直接插入排序。

/*** 希爾排序* @param a */
private static void shellSort(int[] a) {int dk = a.length / 2;while (dk >= 1) {//類似插入排序，只是插入排序增量是 1，這里增量是 dk,把 1 換成 dk 就可以了for (int i = dk; i < a.length; i++) {if (a[i] < a[i - dk]) {int j;int x = a[i];//x 為待插入元素a[i] = a[i - dk];for (j = i - dk; j >= 0 && x < a[j]; j = j - dk) {//通過循環，逐個后移一位找到要插入的位置。a[j + dk] = a[j];}a[j + dk] = x;//插入}}dk = dk / 2;}
}

歸并排序算法

（1）基本思想：歸并（Merge）排序法是將兩個（或兩個以上）有序表合并成一個新的有序表，即把待排序序列分為若干個子序列，每個子序列是有序的。然后再把有序子序列合并為整體有序序列。

（2）歸并排序：是建立在歸并操作上的一種有效，穩定的排序算法。

什么是歸并操作？

歸并操作，也叫歸并算法，指的是將兩個順序序列合并成一個順序序列的方法。
如　設有數列{6，202，100，301，38，8，1}
初始狀態：6,202,100,301,38,8,1
第一次歸并后：{6,202},{100,301},{8,38},{1}，比較次數：3；
第二次歸并后：{6,100,202,301}，{1,8,38}，比較次數：4；
第三次歸并后：{1,6,8,38,100,202,301},比較次數：4；
總的比較次數為：3+4+4=11；
逆序數為14；

示例代碼：

/*** 歸并排序* @param nums 待排序數組* @param l 開始索引：0* @param h 最大索引：nums.length - 1* @return 排序好的數組*/
public static int[] mergeSort(int[] nums, int l, int h) {if (l == h)return new int[]{nums[l]};int mid = l + (h - l) / 2;int[] leftArr = mergeSort(nums, l, mid); //左有序數組int[] rightArr = mergeSort(nums, mid + 1, h); //右有序數組int[] newNum = new int[leftArr.length + rightArr.length]; //新有序數組int m = 0, i = 0, j = 0;while (i < leftArr.length && j < rightArr.length) {newNum[m++] = leftArr[i] <= rightArr[j] ? leftArr[i++] : rightArr[j++];}while (i < leftArr.length)newNum[m++] = leftArr[i++];while (j < rightArr.length)newNum[m++] = rightArr[j++];return newNum;
}

桶排序算法

（1）基本思想：把數組 arr 劃分為 n 個大小相同子區間（桶），每個子區間各自排序，最后合并 。計數排序是桶排序的一種特殊情況，可以把計數排序當成每個桶里只有一個元素的情況。

（2）排序過程：

• 找出待排序數組中的最大值 max、最小值 min
• 我們使用 動態數組 ArrayList 作為桶，桶里放的元素也用 ArrayList 存儲。桶的數量為(maxmin)/arr.length+1
• 遍歷數組 arr，計算每個元素 arr[i] 放的桶
• 每個桶各自排序

示例代碼：

/*** 桶排序** @param data 待排序數組*/
public static void bucketSort(int data[]){int n = data.length;int bask[][] = new int[10][n];int index[] = new int[10];int max = Integer.MIN_VALUE;for (int i = 0; i < n; i++) {max = max > (Integer.toString(data[i]).length()) ? max : (Integer.toString(data[i]).length());}String str;for (int i = max - 1; i >= 0; i--) {for (int j = 0; j < n; j++) {str = "";if (Integer.toString(data[j]).length() < max) {for (int k = 0; k < max - Integer.toString(data[j]).length(); k++)str += "0";}str += Integer.toString(data[j]);bask[str.charAt(i) - '0'][index[str.charAt(i) - '0']++] = data[j];}int pos = 0;for (int j = 0; j < 10; j++) {for (int k = 0; k < index[j]; k++) {data[pos++] = bask[j][k];}}for (int x = 0; x < 10; x++) index[x] = 0;}
}

基數排序算法

（1）基本思想：將整數按位數切割成不同的數字，然后按每個位數分別比較。

（2）排序過程：將所有待比較數值（正整數）統一為同樣的數位長度，數位較短的數前面補零。然后，從最低位開始，依次進行一次排序。這樣從最低位排序一直到最高位排序完成以后,數列就變成一個有序序列。

（3）代碼示例：

/*** 基數排序* @param number 待排序的數組* @param d 表示最大的數有多少位*/
public static void sort(int[] number, int d) 
{int k = 0;int n = 1;int m = 1; //控制鍵值排序依據在哪一位int[][] temp = new int[10][number.length]; //數組的第一維表示可能的余數0-9int[] order = new int[10]; //數組order[i]用來表示該位是i的數的個數while (m <= d) {for (int i = 0; i < number.length; i++) {int lsd = ((number[i] / n) % 10);temp[lsd][order[lsd]] = number[i];order[lsd]++;}for (int i = 0; i < 10; i++) {if (order[i] != 0)for (int j = 0; j < order[i]; j++) {number[k] = temp[i][j];k++;}order[i] = 0;}n *= 10;k = 0;m++;}
}

分治算法

分治算法基本介紹
分治法（Divide-and-Conquer）是一種很重要的算法。字面上的解釋是"分而治之"，就是把一個復雜的問題分成兩個或更多的相同或相似的子問題，再把子問題分成更小的子問題……直到最后子問題可以簡單的直接求解，原問題的解即子問題的解的合并。

這個技巧是很多高效算法的基礎，如排序算法(快速排序，歸并排序)，傅立葉變換(快速傅立葉變換)…

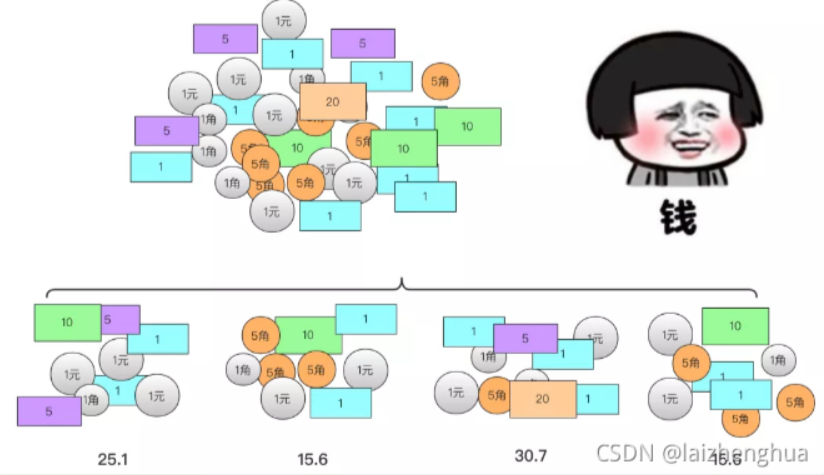
分治算法的基本實現步驟（分治法在每一層遞歸上都有三個步驟）：

1. **分解：**將原問題分解為若干個規模較小，相互獨立，與原問題形式相同的子問題
2. **解決：**若子問題規模較小而容易被解決則直接解，否則遞歸地解各個子問題
3. **合并：**將各個子問題的解合并為原問題的解

漢諾塔問題

分治算法經典問題：漢諾塔問題

漢諾塔的傳說

漢諾塔：漢諾塔（又稱河內塔）問題是源于印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著 64 片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。并且規定，在小圓盤上不能放大圓盤，在三根柱子之間一次只能移動一個圓盤。

假如每秒鐘一次，共需多長時間呢？移完這些金片需要 5845.54 億年以上，太陽系的預期壽命據說也就是數百億年。真的過了 5845.54 億年，地球上的一切生命，連同梵塔、廟宇等，都早已經灰飛煙滅。

體驗完后，我們來整理下移動盤子的思路（假設有A、B、C柱子）：

1、如果只有一個盤，直接可以A->C

2、如果盤子的數量 n >= 2，我就可以看做是兩個盤子。。

• 最下邊（最大）的盤
• 上面的盤

因此就可以走三部曲

先把最上面的盤A->B
把最下邊的盤A->C
把B塔的所有盤從B->C

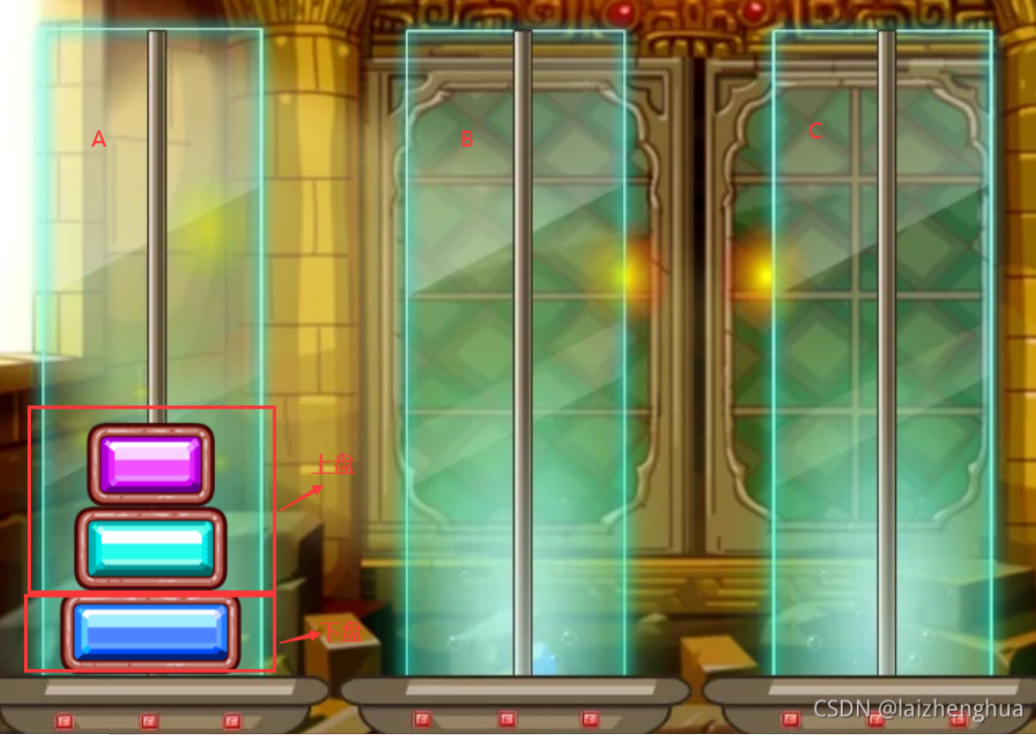
代碼示例：

/*** 漢諾塔問題解決* @param discNum 盤子數量* @param a A柱子* @param b B柱子* @param c C柱子*/
public static void towerOfHanoi(int discNum, char a, char b, char c) {// 如果只有一個盤if (discNum == 1) {System.out.println("第1個盤" + a + "->" + c);} else {// 盤的數量 >= 2// 1.上盤A->BtowerOfHanoi(discNum - 1, a, c, b);// 2.下盤A->CSystem.out.println("第" + discNum + "個盤" + a + "->" + c);// 3.把B柱子的所有盤子移至C柱子towerOfHanoi(discNum - 1, b, a, c);}
}

動態規劃算法

引子

背包問題：現有一個背包，容量為4磅。現有如下物品：

1、要求達到的目標為裝入的背包的總價值最大，并且重量不超出

2、要求裝入的物品不能重復

3.2、動態規劃算法基本介紹
1、動態規劃(Dynamic Programming)算法（簡稱DP算法）的核心思想是：將大問題劃分為小問題進行解決，從而一步步獲取最優解的處理算法

2、動態規劃算法與分治算法類似，其基本思想也是將待求解問題分解成若干個子問題，先求解子問題，然后從這些子問題的解得到原問題的解

3、與分治法不同的是，適合于用動態規劃求解的問題，經分解得到子問題往往不是互相獨立的。 ( 即下一個子階段的求解是建立在上一個子階段的解的基礎上，進行進一步的求解 )

4、動態規劃可以通過填表的方式來逐步推進，得到最優解

代碼實現背包問題

1、背包問題主要是指一個給定容量的背包、若干具有一定價值和重量的物品，如何選擇物品放入背包使物品的價值最大。其中又分 01 背包和完全背包(完全背包指的是：每種物品都有無限件可用)

2、這里的問題屬于 01 背包，即每個物品最多放一個。而無限背包可以轉化為 01 背包。

3、算法的主要思想：利用動態規劃來解決。每次遍歷到的第 i 個物品，根據w[i] 和 v[i] 來確定是否需要將該物品放入背包中。即對于給定的 n 個物品，設 v[i]、w[i]分別為第 i 個物品的價值和重量，C 為背包的容量。再令 v[i][j]表示在前 i 個物品中能夠裝入容量為 j 的背包中的最大價值。

基于以上設定我們得出：

/*
(1) v[i][0]=v[0][j]=0; //表示 填入表 第一行和第一列是 0
(2) 當 w[i]> j時：v[i][j]=v[i-1][j] // 當準備加入新增的商品的容量大于 當前背包的容量時，就直接使用上一個單元格的裝入策略
(3) 當 j>=w[i]時： v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} // 當準備加入的新增的商品的容量小于等于當前背包的容量,裝入的方式:1. v[i-1][j]： 就是上一個單元格的裝入的最大值2. v[i]: 表示當前商品的價值3. v[i-1][j-w[i]]： 裝入 i-1 商品，到剩余空間 j-w[i]的最大值4. 當 j>=w[i]時： v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
*/

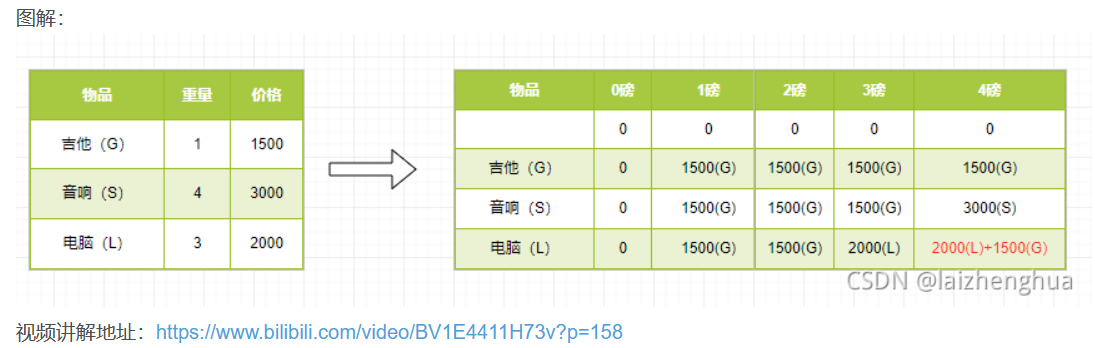
代碼示例：

public static void main(String[] args) {int[] wight = new int[]{1, 4, 3}; // 物品的重量int[] price = new int[]{1500, 3000, 2000}; // 物品的價格int m = 4; // 背包的容量int n = price.length; // 物品的個數// 創建一個二維數組// v[i][j] 表示在前i個物品中能夠裝入容量為j的背包中的最大價值int[][] v = new int[n + 1][m + 1];// 初始化第一行和第一列，這里在本程序中，可以不去處理，因為默認就是0for (int i = 0; i < v.length; i++) {v[i][0] = 0; // 將第一列設置為0}for (int i = 0; i < v.length; i++) {v[0][i] = 0; // 將第一行設置為0}// 為了記錄放入商品的情況，我們定一個二維數組int[][] path = new int[n + 1][m + 1];// 動態規劃處理背包問題// i和j初始都等于1，目的是不處理第一行第一列for (int i = 1; i < v.length; i++) {for (int j = 1; j < v[i].length; j++) {// 公式if (wight[i - 1] > j) { // 因為我們程序i是從1開始的，因此原理公式中的w[i]修改成[i-1]v[i][j] = v[i - 1][j];} else {// 因為 i 是從1開始的，因此公式需要做出調整，如下所示// v[i][j] = Math.max(v[i - 1][j], price[i - 1] + v[i - 1][j - wight[i - 1]]);if (v[i - 1][j] < price[i - 1] + v[i - 1][j - wight[i - 1]]) {v[i][j] = price[i - 1] + v[i - 1][j - wight[i - 1]];// 把當前的情況記錄到pathpath[i][j] = 1;} else {v[i][j] = v[i - 1][j];}}}}// 輸出vfor (int i = 0; i < v.length; i++) {for (int j = 0; j < v[i].length; j++) {System.out.print(v[i][j] + " ");}System.out.println();}// 輸出放入的商品情況int i = path.length - 1; // 行的最大下標int j = path[0].length - 1; // 列的最大下標while (i > 0 && j > 0) {if (path[i][j] == 1) {System.out.printf("第%d個商品放入到背包\n", i);j -= wight[i - 1];}i--;}
}

KMP算法

什么是KMP算法

KMP是Knuth、Morris和Pratt首字母的縮寫，KMP也是由這三位學者發明（1977年聯合發表論文）。

KMP主要應用在字符串的匹配，是一個解決模式串在文本串是否出現過，如果出現過，得出最早出現的位置的經典算法。其主要思想是：當出現字符串不匹配時，可以知道之前已經匹配的文本內容，可以利用這些信息避免從頭再去匹配，從而提高匹配效率。

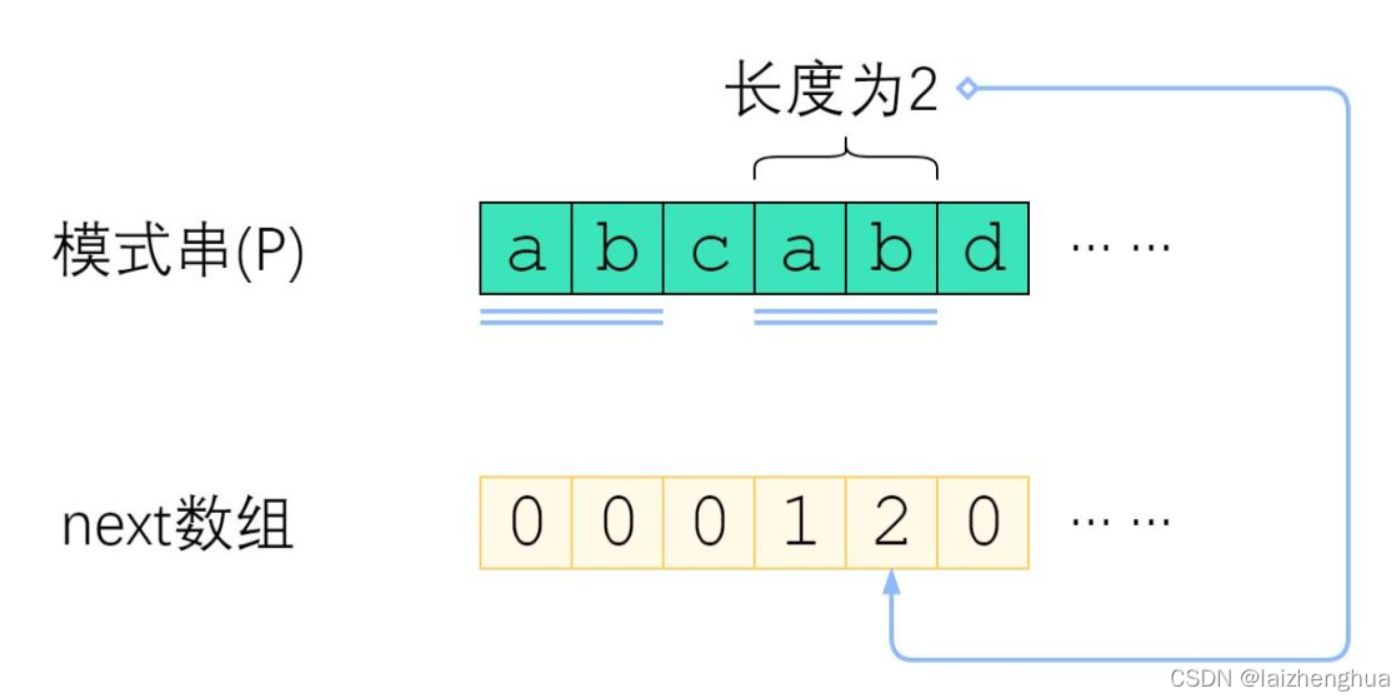
因此如何記錄已經匹配的文本內容，才是KMP的重點~這也使得next數組派上了用場。

KMP算法就利用之前判斷過信息，通過一個 next 數組，保存模式串中前后最長公共子序列的長度，每次回溯時，通過 next 數組找到前面匹配過的位置，省去了大量的計算時間。

暴力匹配

現給出一段字符串str1：“硅硅谷 尚硅谷你尚硅 尚硅谷你尚硅谷你尚硅你好”，和一段子字符串str2：“尚硅谷你”。

要求寫出判斷str1是否含有str2的代碼，如果存在就返回第一次出現的位置，如果沒有則返回-1。

說到字符串匹配，我們第一時間想到的是直接遍歷字符串，看看是否存在。這種方法稱為暴力匹配，拋開效率不說，這種方式是最直接，最簡單的方式。

然而暴力匹配也是一種算法，一種解決方案，針對上述問題，我們可以得出暴力匹配算法的思路（假設現在 str1 匹配到 i 位置，子串 str2 匹配到 j 位置）：

• 如果當前字符匹配成功（即 str1[i] == str2[j]），則 i++，j++，繼續匹配下一個字符
• 如果失配（即 str1[i] != str2[j]），令 i = i - (j - 1)，j = 0。相當于每次匹配失敗時，i 回溯，j 被置為 0
• 用暴力方法解決的話就會有大量的回溯，每次只移動一位，若是不匹配，移動到下一位接著判斷，浪費了大量的時間(不可行!)

代碼示例：

/*** 暴力匹配算法* @param str1* @param str2* @return 返回str2首次出現在str1的位置，匹配不到則返回-1*/
public static int violenceMatch(String str1, String str2) {char[] s1 = str1.toCharArray();char[] s2 = str2.toCharArray();int i = 0; // 指向s1int j = 0; // 指向s2while (i < s1.length && j < s2.length) {if (s1[i] == s2[j]) {i++;j++;} else {// 只要有一個沒有匹配上i = i - (j - 1);j = 0;}}// 判斷是否匹配成功if (j == s2.length) {return i - j;}return -1;
}

在main方法中測試暴力匹配：

public class AlgorithmUtils {public static void main(String[] args) {String str1 = "硅硅谷 尚硅谷你尚硅 尚硅谷你尚硅谷你尚硅你好";String str2 = "尚硅谷你";int index = AlgorithmUtils.violenceMatch(str1, str2);if (index != -1) {System.out.printf("第一次出現的位置是%d", index);}}
}

KMP算法實現

前面呢我們已經使用暴力匹配算法，完成了上述問題的求解！也知道了暴力匹配存在效率問題，那么KMP算法又是怎樣實現呢？

為方便闡述，這里我們換個案例：現有兩組字符串

str1 = “BBC ABCDAB ABCDABCDABDE”;
str2 = “ABCDABD”;

要求使用 KMP算法 完成判斷，str1 是否含有 str2，如果存在，就返回第一次出現的位置，如果沒有，則返回-1。

備注：不能使用簡單的暴力匹配算法！！！