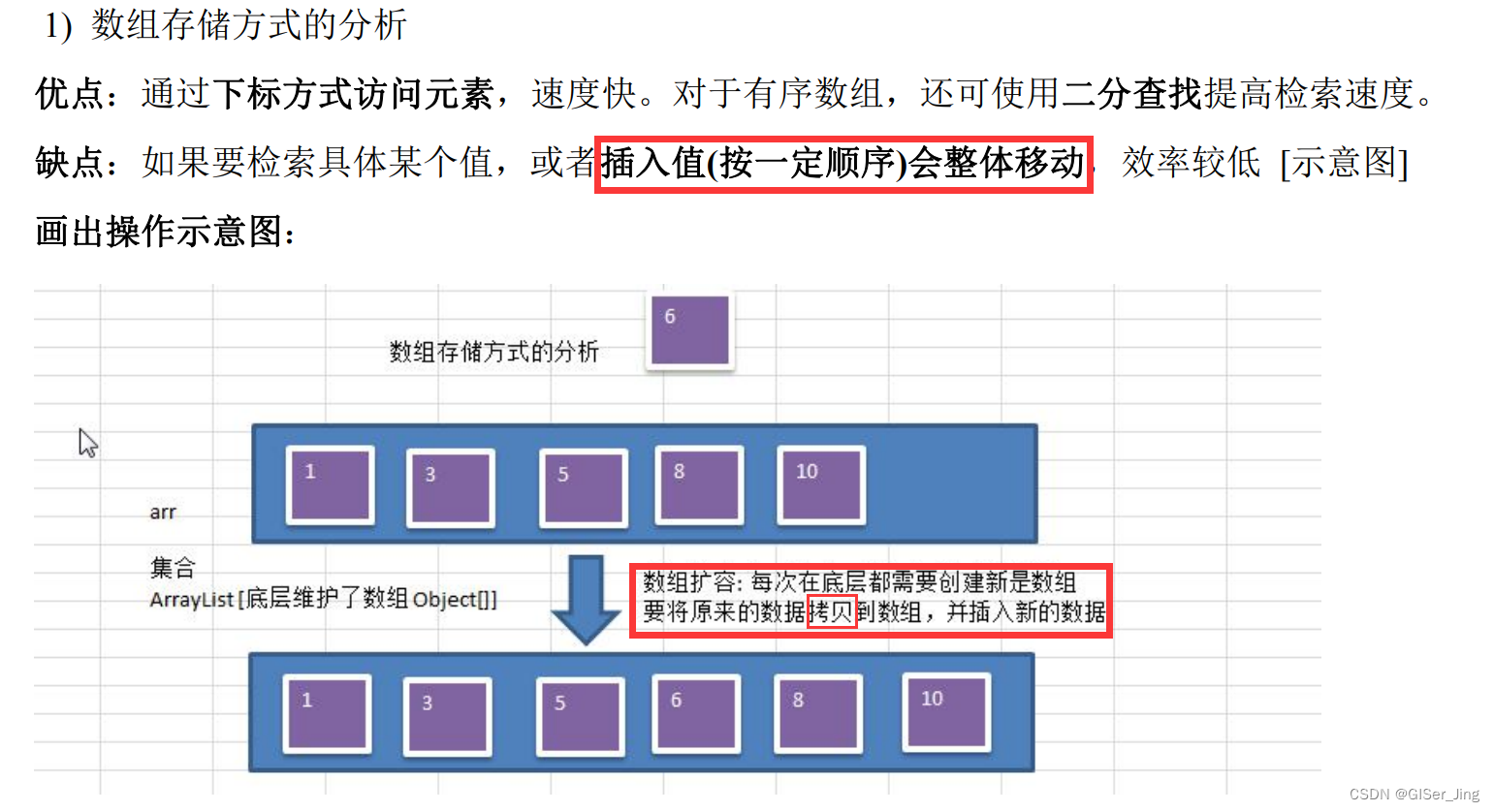
1.why:

數組&鏈表&樹

?

?

2. 大綱

?

2.1前中后序

public class HeroNode {private int no;private String name;private  HeroNode left;//默認為nullprivate HeroNode right;//默認為nullpublic HeroNode(int no, String name) {this.no = no;this.name = name;}public int getNo() {return no;}public void setNo(int no) {this.no = no;}public String getName() {return name;}public void setName(String name) {this.name = name;}public HeroNode getLeft() {return left;}public void setLeft(HeroNode left) {this.left = left;}public HeroNode getRight() {return right;}public void setRight(HeroNode right) {this.right = right;}@Overridepublic String toString() {return "HeroNode{" +"no=" + no +", name='" + name + '\'' +'}';}//遍歷//編寫前序遍歷方法,被誰調用this就是誰public void preOrder(){System.out.println(this);//先輸出父節點//遞歸先左子樹前遍歷if(this.left!=null){this.left.preOrder();}//遞歸向右子樹前序遍歷if (this.right!=null){this.right.preOrder();}};//編寫中序遍歷方法public void infixOrder(){//遞歸先左子樹前遍歷if(this.left!=null){this.left.infixOrder();}//再輸出父節點System.out.println(this);//遞歸向右子樹前序遍歷if (this.right!=null){this.right.infixOrder();}};//編寫后序遍歷方法public void postOrder(){//遞歸先左子樹前遍歷if(this.left!=null){this.left.postOrder();}//遞歸向右子樹前序遍歷if (this.right!=null){this.right.postOrder();}//最后輸出父節點System.out.println(this);};}

2.2查找節點

 //查找//前序查找public HeroNode preSearch(int HeroNo){//判斷當前節點是不是if (this.getNo()==HeroNo){return this;};//左子樹前序查找//如果左遞歸前序查找節點，找到結點，則返回HeroNode resNode = null;//輔助節點if (this.getLeft()!=null) {resNode =this.getLeft().preSearch(HeroNo);}//resNode不為空才返回，因為右子樹仍未查找if (resNode!=null){return resNode;}if (this.getRight()!=null){resNode = this.getRight().preSearch(HeroNo);}return resNode;}//中序查找public HeroNode infixSearch(int HeroNo){//左子樹前序查找//如果左遞歸前序查找節點，找到結點，則返回HeroNode resNode = null;//輔助節點if (this.getLeft()!=null) {resNode =this.getLeft().preSearch(HeroNo);}//resNode不為空才返回，因為右子樹仍未查找if (resNode!=null){return resNode;};//判斷當前節點是不是if (this.getNo()==HeroNo){return this;}//查找右子樹if (this.getRight()!=null){resNode = this.getRight().preSearch(HeroNo);}return resNode;}//后序查找public HeroNode postSearch(int HeroNo){//左子樹前序查找//如果左遞歸前序查找節點，找到結點，則返回HeroNode resNode = null;//輔助節點if (this.getLeft()!=null) {resNode =this.getLeft().preSearch(HeroNo);}//resNode不為空才返回，因為右子樹仍未查找if (resNode!=null){return resNode;};if (this.getRight()!=null){resNode = this.getRight().preSearch(HeroNo);}if (resNode!=null){return resNode;};//最后判斷當前節點是不是if (this.getNo()==HeroNo){return this;};return resNode;}

2.3刪除節點（基本）?

//刪除public void deleteNode(int HeroNo){//判斷左子節點if (this.left!=null && this.left.getNo()==HeroNo){this.left=null;return;}//判斷右子節點if (this.right!=null&&this.right.getNo()==HeroNo){this.right=null;return;}//遍歷左子樹if (this.left!=null){this.left.deleteNode(HeroNo);}if(this.right!=null){this.right.deleteNode(HeroNo);}}

2.4二叉樹 （root節點）

public class BinaryTree {//rootprivate HeroNode root;public void setRoot(HeroNode root) {this.root = root;};//遍歷二叉樹//前序遍歷public void preOrder(){if (this.root!=null){this.root.preOrder();}else {System.out.println("二叉樹為空");}}//中序遍歷public void infixOrder(){if (this.root!=null){this.root.infixOrder();}else {System.out.println("二叉樹為空");}}//后續遍歷public void postOrder(){if (this.root!=null){this.root.postOrder();}else {System.out.println("二叉樹為空");}}//查找二叉樹指定節點//前序查找public HeroNode preSearch(int HeroNo){if (this.root!=null){return this.root.preSearch(HeroNo);}else {return null;}}//中序查找public HeroNode infixSearch(int HeroNo){if (this.root!=null){return this.root.infixSearch(HeroNo);}else {return null;}}//后序查找public HeroNode postSearch(int HeroNo){if (this.root!=null){return this.root.postSearch(HeroNo);}else {return null;}}public void delNode(int HeroNo){if(root!=null){if (root.getNo()==HeroNo){root=null;}else {root.deleteNode(HeroNo);}}else {System.out.println("空樹，無法刪除");}}
}

2.5順序存儲二叉樹??（為完全二叉樹，公式）

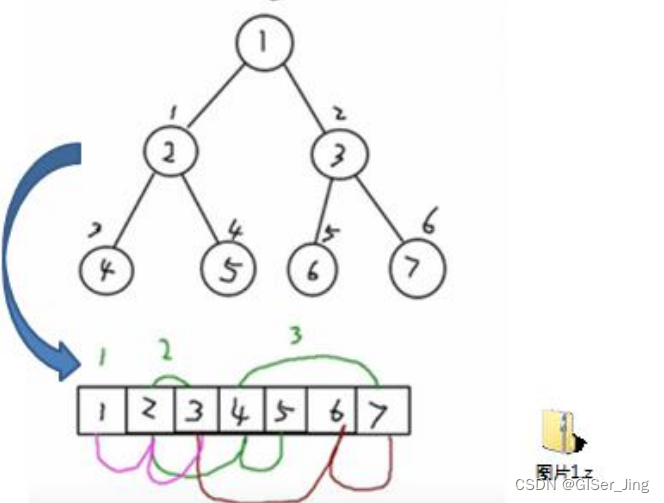
public class ArrBinaryTree {private int [] arr;//存儲結點的數組public ArrBinaryTree(int[] arr) {this.arr = arr;}//重載public void preOrder(){preOrder(0);}public void infixOrder(){infixOrder(0);}/**** @param index  arr[index]=i*///前序public void preOrder(int index){if(arr == null ||arr.length==0){System.out.println("數組為空");}System.out.println(arr[index]);//向左遞歸遍歷if ((index*2+1)<arr.length){preOrder(2*index+1);}//向右遞歸遍歷if ((index*2+2)<arr.length){preOrder(2* index+2);}}//中序public void infixOrder(int index){if(arr == null ||arr.length==0){System.out.println("數組為空");}//向左遞歸遍歷if ((index*2+1)<arr.length){infixOrder(index*2+1);}System.out.println(arr[index]);//向右遞歸遍歷if ((index*2+2)<arr.length){infixOrder(2* index+2);}}
}

?2.6線索化二叉樹（節點左右節點類型、前驅指針）

?

?

public class ThreadBinaryTree {private HeroNode root;//為了實現線索化，需要創建要給指向當前結點的前驅結點的指針// 在遞歸進行線索化時，pre總是保留前一個結點//pre指針private HeroNode pre =null;public HeroNode getRoot() {return root;}public HeroNode getPre() {return pre;}public void setPre(HeroNode pre) {this.pre = pre;}public void setRoot(HeroNode root) {this.root = root;};//重載threadNodes()public void threadedNodes(){this.threadedNodes(root);}/*多回顧*/
//    //中序線索化二叉樹public void threadedNodes(HeroNode node){//遞歸找到最左節點，然后返回if (node == null) {return;}//先線索化左子樹threadedNodes(node.getLeft());//線索化當前節點if (node.getLeft()==null){node.setLeft(pre);node.setLeftType(1);}//key！！！if (pre!=null&&pre.getRight()==null){pre.setRight(node);pre.setRightType(1);}pre=node;//線索化右子樹threadedNodes(node.getRight());};//***提高：中序、后序***//遍歷線索化二叉樹public void threadedList(){HeroNode node = root;while (root!=null){while(node!=null){//循環的找到leftType ==1的結點，第一個找到就是8結點// 后面隨著遍歷而變化,因為當leftType==1時，說明該結點是按照線索化// 處理后的有效結點while (node.getLeftType()==0){node=node.getLeft();}System.out.println(node);while (node.getRightType()==1){node=node.getRight();System.out.println(node);}//替換這個遍歷點（對于原本就有右結點的）!!!node=node.getRight();}}}//遍歷二叉樹//前序遍歷public void preOrder(){if (this.root!=null){this.root.preOrder();}else {System.out.println("二叉樹為空");}}//中序遍歷public void infixOrder(){if (this.root!=null){this.root.infixOrder();}else {System.out.println("二叉樹為空");}}//后續遍歷public void postOrder(){if (this.root!=null){this.root.postOrder();}else {System.out.println("二叉樹為空");}}//查找二叉樹指定節點//前序查找public HeroNode preSearch(int HeroNo){if (this.root!=null){return this.root.preSearch(HeroNo);}else {return null;}}//中序查找public HeroNode infixSearch(int HeroNo){if (this.root!=null){return this.root.infixSearch(HeroNo);}else {return null;}}//后序查找public HeroNode postSearch(int HeroNo){if (this.root!=null){return this.root.postSearch(HeroNo);}else {return null;}}public void delNode(int HeroNo){if(root!=null){if (root.getNo()==HeroNo){root=null;}else {root.deleteNode(HeroNo);}}else {System.out.println("空樹，無法刪除");}}
}

?