目錄

• 棧的概念及結構
• 棧的實現
• • 初始化棧
  • 入棧
  • 出棧
  • 其他一些棧函數
• 小結
• 棧相關的題目

棧的概念及結構

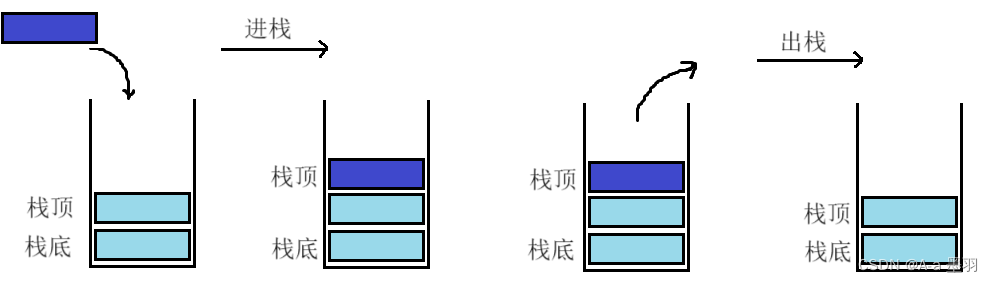
棧是一種特殊的線性表。相比于鏈表和順序表，棧只允許在固定的一端進行插入和刪除元素操作。進行數據插入和刪除操作的一端稱為棧頂，另一端稱為棧底。棧中的數據元素遵守后進先出LIFO（Last In First Out）的原則。

• 壓棧：棧的插入操作叫做進棧/壓棧/入棧，入數據在棧頂。
• 出棧：棧的刪除操作叫做出棧。出數據也在棧頂。

聯想一下，其實棧就相當于手槍的彈夾，將子彈壓入彈夾的操作就相當于壓棧，打出子彈的操作就相當于出棧，每次先打出的子彈都是我們最后壓入彈夾的子彈，最后一顆子彈就是我們最先壓入的那一顆了，這就是后進先出。棧也如此，結構大致如下：

基于這樣的結構，那么如果我們想要拿到棧的某個元素，就必須要先把此元素以上的元素依次出棧，然后才能取出。

棧的實現

有兩種方式可以實現棧結構-數組棧，鏈式棧：

1. 鏈式棧
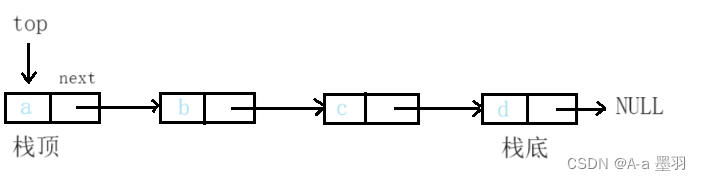
   如果用單鏈表實現：若棧底就指向頭節點，棧頂就指向尾節點。這樣設計入棧很方便，相當于頭插，時間復雜度為O(1)；但出棧操作就必須要先遍歷鏈表找到棧頂的前一個，然后再出棧，并修改棧頂，相當于尾刪，時間復雜度達到O(N)。于是乎我們一般將棧頂指向頭節點，棧底指向尾節點，這樣入棧出棧就都是O(1)了，即頭插/頭刪。

如果用雙向鏈表實現：棧頂為鏈表的頭和尾都可以，入棧和出棧時間復雜度都為O(1)，但雙向鏈表結構較為復雜，一般不選用此結構

2. 數組棧
   數組棧的入棧和出棧的實現較為簡單，且時間復雜度為O(1)

相較于鏈式棧，數組棧訪問數據時cpu緩存命中率比較高，但鏈式棧相較于數組棧也會節省一定的空間。下面棧的實現主要用的是數組棧。
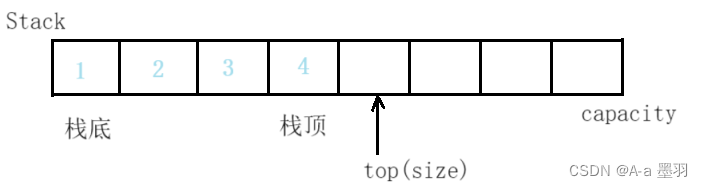
通常我們標識棧頂位置的下一個位置為top(即下標為size的位置)。與標識棧頂位置為top相比較，這樣可以減少棧為空，棧容量判斷等函數的難度，且若標識棧頂位置為top，當棧里面沒有元素時top的指向也較為尷尬。
我們可以如下定義棧結構：

typedef int STDataType;
//數組棧
typedef struct stack
{STDataType* a;int top;//標識棧頂下一個元素下標（同為棧元素個數）int capacity;
}ST;

初始化棧

通過上面對棧的介紹進行初始化。

//初始化
void StackInit(ST* pst)
{assert(pst);pst->top = 0;pst->capacity = 0;pst->a = NULL;
}

入棧

入棧操作就是向數組內增加一個數，首先要判斷棧（數組）容量pst->capacity是否需要增容，然后向top位置（即pst->a[top]）增加一個數，最后重新變換top指向（即pst->top++），具體如下：

//入棧
void StackPush(ST* pst, STDataType x)
{assert(pst);//判斷增容if (pst->top == pst->capacity){int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;STDataType* newnode = (STDataType*)realloc(pst->a, sizeof(ST) * newcapacity);if (newnode == NULL){perror("check_ST_capacity()::malloc");return;}pst->a = newnode;pst->capacity = newcapacity;}//目標數x入棧pst->a[pst->top] = x;//變換top指向pst->top++;
}

出棧

出棧操作就相對簡單了，直接改變top指向就可以了（即pst->top--）。如果棧里面已經沒有元素了，那執行此操作top指向就會錯誤，于是乎我們需要斷言一下來確保棧里面有元素可以刪除（即assert(ps->top != 0);）。

//出棧
void StackPop(ST* pst)
{assert(pst);assert(pst->top != 0);pst->top--;
}

其他一些棧函數

1. 獲得棧頂元素：
   pst->top指向的是棧頂的下一個元素的下標，那么只需要讓他--即可（即pst->a[pst->top-1]），在使用前確保棧中有元素，不然程序會崩潰（越界訪問）。

// 獲取棧頂元素 
STDataType StackTop(ST* pst)
{assert(pst);assert(pst->top != 0);return pst->a[pst->top - 1];
}

2. 獲得棧有效元素個數：
   pst->top指向的既是指向棧頂下一個元素的下標也是整個棧里面有效數據的個數，所以此函數返回pet->top即可。

// 獲取棧中有效元素個數
int StackSize(ST* pst)
{assert(pst);return pst->top;
}

3. 檢查棧是否為空：
   同理只要棧里面有效元素個數為0，那么棧就是空棧，如下：

// 檢測棧是否為空，如果為空返回非零結果，如果不為空返回0 
bool StackEmpty(ST* pst)
{assert(pst);return pst->top == 0;
}

4. 棧的銷毀：
   棧的銷毀本質上是釋放先前realloc()開辟的數組，再將容量和棧頂置0即可。

// 銷毀棧 
void StackDestroy(ST* pst)
{assert(pst);assert(pst->capacity != 0);free(pst->a);pst->a = NULL;pst->top = pst->capacity = 0;
}

---

小結

• 棧是一種后進先出的結構，這一點恰與我們后面要講的隊列相反；

• 順序表和鏈表都可以用來實現棧，不過一般都使用順序表，因為棧想當于是閹割版的順序表，只用到了順序表的尾插和尾刪操作，順序表的尾插和尾刪不需要搬移元素,因此效率非常高O(1)，故一般都是使用順序表實現；

• 棧結構中的top一般為要插入位置的下標（即棧頂元素下一個位置），這是為了方便區分棧為空棧的情況，且后續函數更好實現；

• 棧只能在棧頂進行輸入的插入和刪除操作，不支持隨機訪問；

---

棧相關的題目

1. 關于入棧和出棧順序，如下：

若進棧序列為 1,2,3,4 ，進棧過程中可以出棧，則下列不可能的一個出棧序列是（）
A 1,4,3,2
B 2,3,4,1
C 3,1,4,2
D 3,4,2,1

不難看出是c選項錯了，因為如果第一個出棧的是3，那么在3之前壓棧的1和2就都還沒有出棧，所以接下來出棧的只能有兩種情況：

• 1.4接著入棧然后出棧，即為D選項；
• 2.直接出先前壓棧的2。

對于C選項，此時的1還在棧底，在它上面還有2，所以不能直接出1。

2. LeetCode OJ題： 有效的括號

題目描述：給定一個只包括 '('，')'，'{'，'}'，'['，']'的字符串s ，判斷字符串是否有效。
有效字符串需滿足：

• 左括號必須用相同類型的右括號閉合。
• 左括號必須以正確的順序閉合。
• 每個右括號都有一個對應的相同類型的左括號。

這題主要考察我們對棧特性的應用，即后進先出，那么我們便可這樣設計：循環遍歷字符串s中的每個字符，滿足以下條件的對棧進行入/出棧操作：

1. 遇到左括號，直接入棧；
2. 遇到右括號，取棧頂元素進行匹配，若不匹配直接返回false，若匹配就將此括號出棧，并繼續循環。

另外我們還要對如下兩種情況做出判斷：

1. 當遍歷到右括號時，此時棧中是否還有元素？（QueueEmpty()?）為空直接返回false；
2. 當字符串s遍歷結束時，棧中是否還有剩余元素？（QueueEmpty()?）不為空直接返回false，為空返回true。

其中一些棧的接口函數就不展示了，上面內容都有，代碼實現如下：

bool isValid(char* s)
{ST st;//創建棧StackInit(&st);//初始化棧//遍歷字符串swhile(*s){if(*s == '(' || *s == '[' || *s == '{'){StackPush(&st,*s);}else{//棧為空判斷，為空返回false，如上講解1處if(StackEmpty(&st)){StackDestroy(&st);return false;}char ch = StackTop(&st);//左右括號匹配判斷，匹配錯誤返回falseif((*s == ')' && ch != '(') || (*s == ']' && ch != '[') ||(*s == '}' && ch != '{')){StackDestroy(&st);return false;}StackPop(&st);}s++;}//棧為空判斷，不為空返回false,與上面判斷處區分，如上講解2處if(!StackEmpty(&st)){StackDestroy(&st);return false;}return true;
}