優質博文：IT-BLOG-CN

一、題目

給你二叉樹的根節點root，返回其節點值的 層序遍歷 。（即逐層地，從左到右訪問所有節點）。

示例 1：

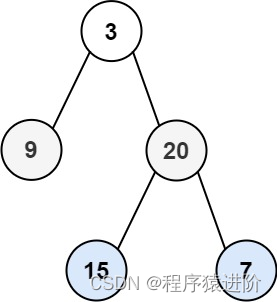
輸入：root = [3,9,20,null,null,15,7]
輸出：[[3],[9,20],[15,7]]

示例 2：
輸入：root = [1]
輸出：[[1]]

示例 3：
輸入：root = []
輸出：[]

樹中節點數目在范圍[0, 2000]內
-1000 <= Node.val <= 1000

二、代碼

廣度優先搜索： 我們可以用廣度優先搜索解決這個問題。我們可以想到最樸素的方法是用一個二元組(node, level)來表示狀態，它表示某個節點和它所在的層數，每個新進隊列的節點的level值都是父親節點的level值加一。最后根據每個點的level對點進行分類，分類的時候我們可以利用哈希表，維護一個以level為鍵，對應節點值組成的數組為值，廣度優先搜索結束以后按鍵level從小到大取出所有值，組成答案返回即可。

考慮如何優化空間開銷：如何不用哈希映射，并且只用一個變量node表示狀態，實現這個功能呢？

我們可以用一種巧妙的方法修改廣度優先搜索：
1、首先根元素入隊
2、當隊列不為空的時候：求當前隊列的長度si；依次從隊列中取si個元素進行拓展，然后進入下一次迭代；

它和普通廣度優先搜索的區別在于，普通廣度優先搜索每次只取一個元素拓展，而這里每次取si個元素。在上述過程中的第i次迭代就得到了二叉樹的第i層的si個元素。

為什么這么做是對的呢？我們觀察這個算法，可以歸納出這樣的循環不變式：第i次迭代前，隊列中的所有元素就是第i層的所有元素，并且按照從左向右的順序排列。證明它的三條性質（你也可以把它理解成數學歸納法）：
【1】初始化： i=1的時候，隊列里面只有root，是唯一的層數為1的元素，因為只有一個元素，所以也顯然滿足「從左向右排列」；
【2】保持： 如果i=k時性質成立，即第k輪中出隊sk的元素是第k層的所有元素，并且順序從左到右。因為對樹進行廣度優先搜索的時候由低k層的點拓展出的點一定也只能是k+1層的點，并且k+1層的點只能由第k層的點拓展到，所以由這sk個點能拓展到下一層所有的sk+1個點。又因為隊列的先進先出（FIFO）特性，既然第k層的點的出隊順序是從左向右，那么第k+1層也一定是從左向右。至此，我們已經可以通過數學歸納法證明循環不變式的正確性。
【3】終止： 因為該循環不變式是正確的，所以按照這個方法迭代之后每次迭代得到的也就是當前層的層次遍歷結果。至此，我們證明了算法是正確的。

class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> ret = new ArrayList<List<Integer>>();if (root == null) {return ret;}Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);while (!queue.isEmpty()) {List<Integer> level = new ArrayList<Integer>();int currentLevelSize = queue.size();for (int i = 1; i <= currentLevelSize; ++i) {TreeNode node = queue.poll();level.add(node.val);if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}ret.add(level);}return ret;}
}

時間復雜度： 每個點進隊出隊各一次，故漸進時間復雜度為O(n)
空間復雜度： 隊列中元素的個數不超過n個，故漸進空間復雜度為O(n)