前言：在學習二叉樹的時候我們基本上已經了解過二叉樹的三種遍歷，對于這三種遍歷，我們采用遞歸的思路，很簡單的就能實現，那么如何用迭代的方法去解決問題？

我們首先來看第一個：

前序遍歷

144. 二叉樹的前序遍歷 - 力扣（LeetCode）

前序遍歷就是以 根 左子樹 右子樹的順序遍歷二叉樹。呢么如何用得帶去解決問題呢？

首先我們知道函數遞歸就是函數一層層的調用自己，本質上是以一種先進后退的思路，而這與棧的特性一致，因此函數遞歸，我們可以用調用堆棧來看，就是棧的思路。

現在我們解決問題，既然不用遞歸，但還是可以用到解決問題的本質思路，就是用棧去解決問題：

例圖：

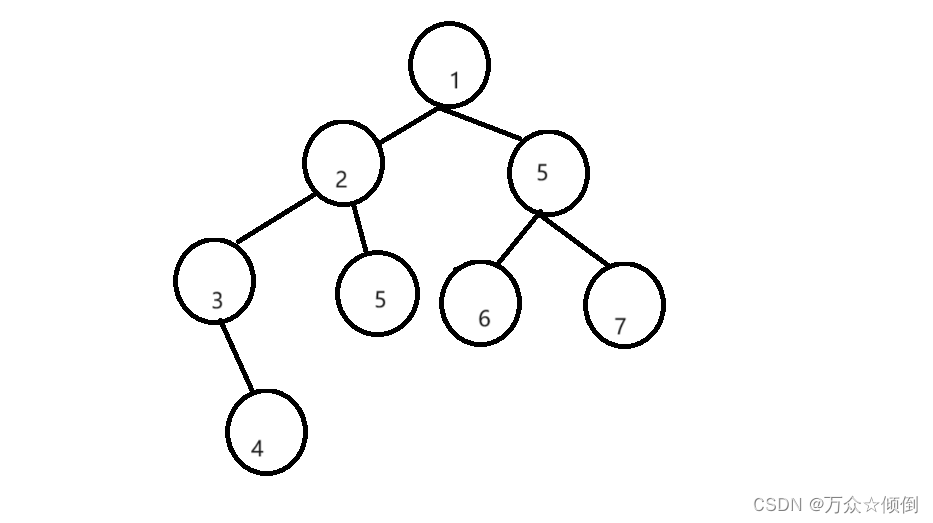
?我們就用這個圖做演示：

大致解題思路：由于二叉樹遍歷一直往下走，無法回頭，我們需要提供一個棧，假設我們每次先遍歷左子樹，每次遍歷的時候，將我們需要往回遍歷的節點放入棧中（往回遍歷的節點就是擁有右子樹的系點），在遍歷完左節點后，此時回退上一個節點，看他的右子樹是否為空。

且我們的整個循環的條件中 棧是否為空 就決定是否繼續遍歷這一個二叉樹。

首先前序遍歷的順序 是根? 左子樹 右子樹 。其次，對于二叉樹，解決了整個左子樹的遍歷。那么整個右子樹的遍歷，也是與之相同的，也就是我們再解決問題時就只針對一個子樹，這里我們就以遍歷整個左子樹為主，實現對整個樹的遍歷。且題目要求返回數組，因此我們是遍歷插入數據。

由于我們無法知道某個左節點的右節點是否為空，所以開始我們先將所有左節點入棧：

第一步操作：

首先要遍歷根，也就是從1開始，不為空，放入數組，并入棧，在看它的左，2不為空，放入數組，并入棧，再看它的左，3，不為空，放入數組并入棧。我們就完成了第一步，但是對于最后一個最左節點（它可能是一個子樹的根，他也有可能是子樹的左節點）。

第二步操作：

從這里開始，我們就要開始判斷是否出棧，此時獲取當前棧頂元素，3節點，再出棧。（此時棧不為空）

? ?若3節點無右節點，此時根已經遍歷完了，現在輪到左子樹了，而3此時是作為一個子樹的左節點，并且是遍歷順序左子樹中的第一個節點，之后出棧，看節點2的右子樹是否存在。

? ?若3節點有右節點（右子樹），比如我們這里就是節點4,3節點就往右子樹走，按照前序遍歷順序，我們該將此節點數據放入數組中，因此以該節點為開始，繼續第一步操作，將該右節點（也有可能是右子樹）,按照先把左節點入棧，入數組，在判斷右子樹情況來出棧。

第三步操作：

其實我們的前序遍歷已經實現，可能有人還覺得還沒完成，因為右子樹還沒處理，實際上當我們回退二叉樹,也就是出棧的時候，出到最后一個元素，也就是真正的根節點時，棧不為空，循環還沒結束，會繼續判斷當前節點的右子樹。

代碼實現：

vector<int> preorderTraversal(TreeNode* root) {//用來返回遍歷結果的數組vector<int> v;//用棧來回退我們二叉樹stack<TreeNode*> t;TreeNode*node=root;//當節點為空或者棧不為空的時候循環繼續while(node||!t.empty()){//第一步將左邊的節點一次放入數組并入棧 while(node){v.push_back(node->val);t.push(node);node=node->left;}//從該位置開始判斷是否要出棧node=t.top();t.pop();if(node->right==nullptr){node=nullptr;//直接為空，繼續循環進入到出棧操作}else{node=node->right;}      }return v;}

中序遍歷

中序遍歷 的順序是?左節點 根 右子樹 。與前序的插入思想不太一樣，不過還是利用棧來回到上一個節點。前序遍歷時，其實是有點巧合，因為根節點與左節點連續，我們是直接將左節點一個個入棧后，直接放入數組，因為順序是從根節點開始，且根節點下來就是左節點，因此插入順序與我們的直接將左節點插入的順序一致。

但對于中序和后序遍歷，都是先從左節點開始的，因此，從根開始，我們是先將之后的左節點一個個入棧，這里就不能再放數組了，直到最左節點時，根據我們的的遍歷順序，下來時根節點，再來判斷。具體分析如下：

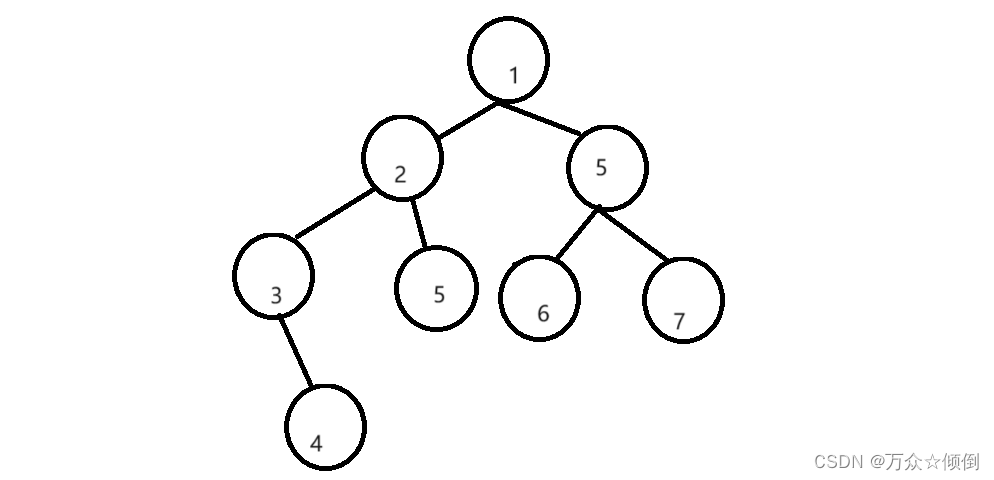
還是以這張圖為例：

第一步：

剛開始我們還是直接以根為開始，將它的一個個左節點入棧，此時棧中為3，2，1。

第二步：

從這里開始，就需要判斷是否出棧，是否插入數組，因此從這里開始，還是先獲取棧頂元素，在出棧，當前位置就是節點3，之后就是判斷3節點是否具有右子樹。

若沒有右子樹，那么3就是第一個左節點，放入數組，之后回退到上一個節點2，繼續判斷。

若有右子樹，此時節點3是一個根，不能放入數組，我們繼續走到節點4，以4節點為開始，與前序遍歷一樣，執行第一步的操作進行入棧，之后在判斷。

直到回退到根節點，此時進行右子樹的遍歷。

代碼如下：

  vector<int> inorderTraversal(TreeNode* root) {vector<int> v;stack<TreeNode*> t;TreeNode* prev=nullptr;while(root||!t.empty()){while(root){if(root){t.push(root);}root=root->left;}root=t.top();t.pop();      //為空先插左節點v.push_back(root->val);if(root->right==nullptr){root=nullptr;}else{root=root->right;}}return v;}

?后序遍歷

后序遍歷的思路與中序遍歷有些許一樣，但對于情況的判斷更加復雜。

因為后序的遍歷順序為 左子樹? 右子樹 根，育賢婿一樣，我們還是從根節點開始，入棧左子樹的所有左節點，直到最左節點，還是要進行判斷。具體分析如下：

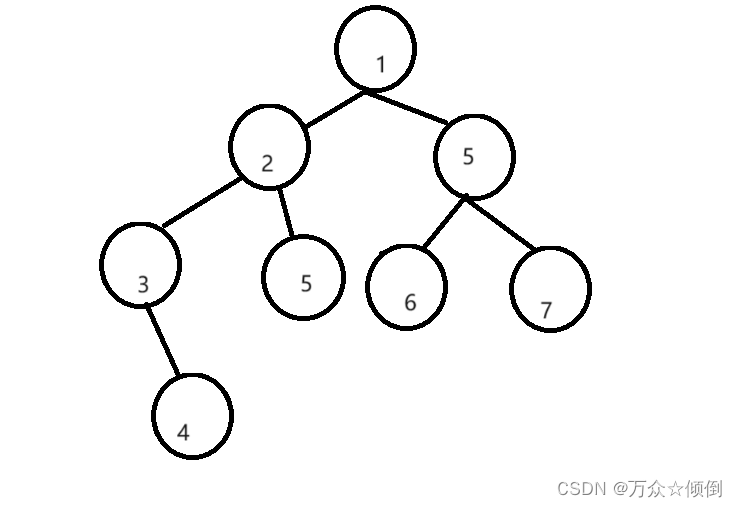
?還是一這張圖為例：

第一步：

依然是將左子樹的所有的左節點依次入棧， 1入，2入，3入，此時到了節點3。

第二步：

從節點3開始判斷是否要回退，因此獲取棧頂節點為3，出棧，當前節點為3。

若3沒有右節點，此時我們就是左節點，我們就可以將3放入數組，之后回退到節點2。

若3的右節點存在，此時的操作是將該節點再次重新入棧（因為下一個右節點（右子樹）插入完才輪到我），之后當前節點走到這個右節點，循環回到第一步，繼續入棧。

在這里有重要的一點：

第一點：與之前兩種遍歷一樣，我們需要從當前節點回退到上個節點的方法是將指針置空，之后重新賦值為棧頂元素的節點。

其次除了葉子節點容易判斷插入，如果上一次插入的節點，是當前節點的右節點，則就需要放入數組里，即 先插的左， 之后插的右，根節點需要判斷，當前節點的右節點是上一次插入的節點就說明是根，插入數組。

源碼：

vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*>s;vector<int> ret;TreeNode*prev=nullptr;while(root||!s.empty()){//先找所有的左節點while(root){ s.push(root);root=root->left;}//倒退判斷這些節點的右節點，直到最后根節點，在判斷右子樹root=s.top(); s.pop();if(root->right==nullptr ||root->right==prev) {ret.push_back(root->val);prev=root;root=nullptr;}else{//若右子樹不為空，繼續入棧s.push(root);root=root->right;}}return ret;}