一、說明

????????歡迎回到這個三部曲的第二部分！在第一部分中，我們為測度論概率奠定了基礎。我們探索了測量和可測量空間的概念，并使用這些概念定義了概率空間。在本文中，我們使用測度論來理解隨機變量。

????????作為一個小回顧，在第一部分中，我們看到概率空間可以使用測度理論按以下方式定義：

????????現在，我們將考慮范圍擴展到隨機變量。在學校中，通常引入隨機變量作為其值是隨機的變量。例如，擲骰子的結果可以通過隨機變量X建模，其值隨機為 1、2、3、4、5 或 6。雖然這個定義適用于概率的基本應用，但它是一點也不嚴謹，并且錯過了一些非常令人滿意的直覺。

二、可測量的功能

????????因此，我們現在轉向測度理論來定義隨機變量。為了做到這一點，我們必須定義一個可測量的函數：

????????讓我們分解一下這個定義。首先，與任何其他函數一樣，可測量函數將一個集合中的元素映射到另一個集合。但這還不是全部，這個函數還有更多維度。函數f的域和余域都是分別配備有 σ 代數 ? 和 ? 的可測空間。而且，最重要的是，可測量函數可以將測量從域的可測量空間“傳輸”到共域的可測量空間。這是什么意思？假設可測空間(F, ? ) 的測度為μ。然后，我們可以應用f來獲得可測空間 (M, ?) 的測度。如何？出色地，

????????而且，我們已經定義了一個可測函數，f?1(?A)肯定屬于F的 σ 代數，因此可以通過測度 μ 來指定。

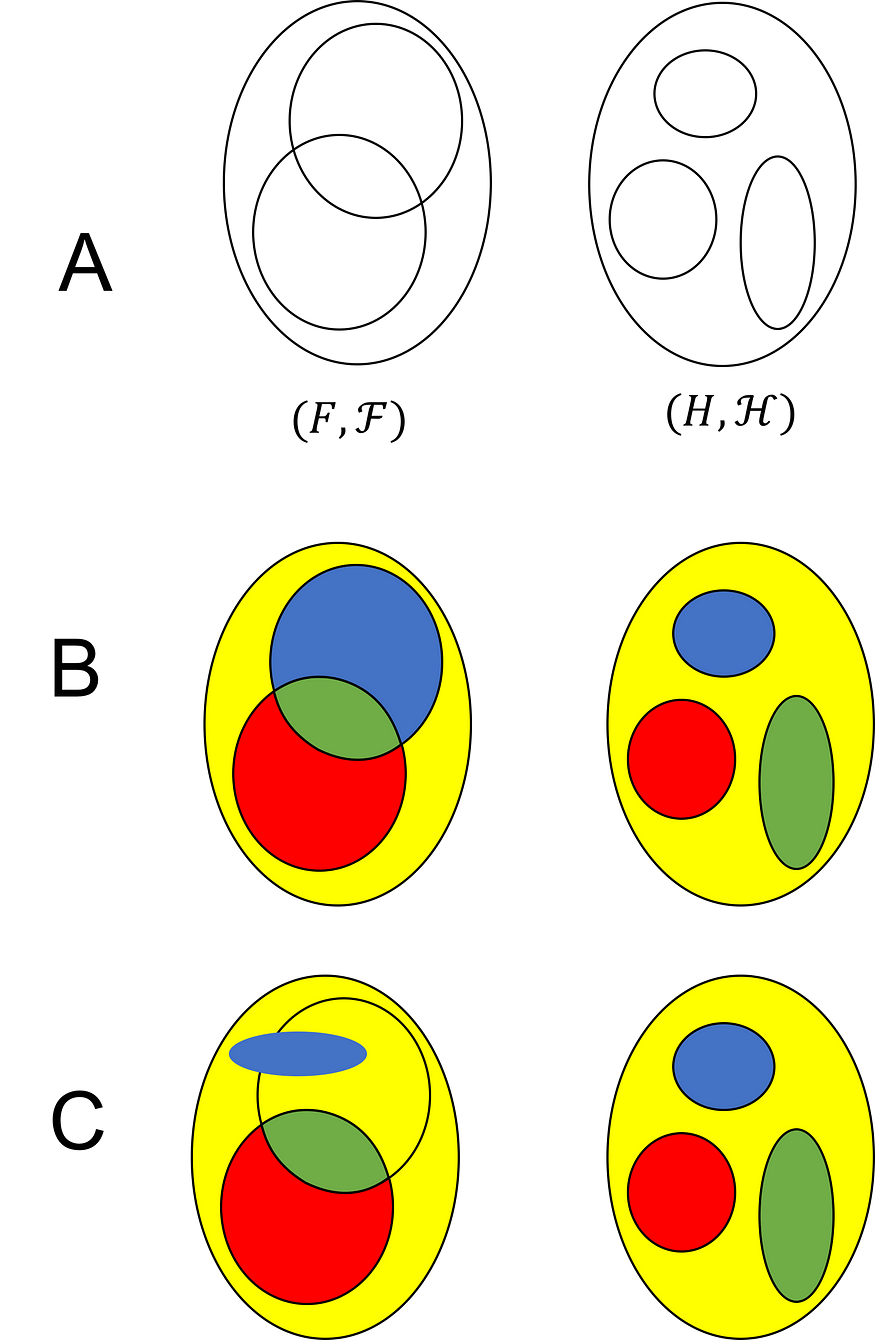
圖片來源：馬修·伯恩斯坦

????????該圖的 A 部分描繪了兩個可測量空間(F,?)和(H,?)。σ 代數由黑線概述的集合生成。B 部分描述了將F映射到H的有效可測量函數f。即，左邊的集合是域，右邊的集合是共域。顏色說明f下F和H的子集之間的圖像關系。例如，F中的藍色集合的圖像是H中的藍色集合。我們看到?的每個成員都有一個可測量的原像。C 部分描述了一個不可測量的函數。該函數是不可測量的，因為?中的藍色集具有不屬于 ? 成員的原像。

三、隨機變量

????????現在我們已經定義了可測量函數，我們可以開始處理隨機變量。使用測度論，我們按以下方式定義隨機變量：

????????這說明了什么？簡而言之，隨機變量是將概率空間中的元素映射到可測量空間的函數。如果您還記得的話，集合 Ω 稱為樣本空間，代表所有可能的未來。隨機變量X簡單地將每個可想象的未來映射到某個集合F中的元素。集合F是X可以取的所有可能值的集合。隨機變量是概率空間中的可測量函數，因為它允許我們將概率測量從概率空間“傳輸”到我們正在考慮的X結果集。

四、離散隨機變量

????????為了說明這一點，我們考慮拋硬幣。令Y為隨機變量，代表拋擲一枚公平硬幣的結果。然后，集合 Ω 代表所有可能的未來——硬幣在空中旋轉、著陸、彈跳等的無限種方式。隨機變量將每個未來映射到可測量的空間(H, ?)，其中H:={ 0,1}。在這里，我們將反面編碼為 0，將正面編碼為 1。例如，硬幣可以有兩種方式a和b，其中硬幣在空中翻轉并落地為正面。那么X(a)=1并且X(b)=1。

????????H 上的 σ 代數表示我們希望為其分配概率的所有結果組：

????????這里需要注意的是，?中的每個元素在原始概率空間中的X下都有一個原像，即該原像是E的成員。因此，我們可以根據測度為?中的每個集合分配一個概率根據P得到其原像：

用熟悉的表示法來說，這很簡單：P(X=1)。

五、連續隨機變量

????????現在，我們轉向連續隨機變量。這有一個稍微不同的方法，因為，很明顯，如果我們采用與離散隨機變量相同的方法，我們將遇到數學矛盾。

????????連續隨機變量還將集合 Ω 中的元素映射到集合H。但在這種情況下，H是所有實數的集合。那是，

????????現在的問題是，我們不能像對待離散隨機變量那樣擁有 σ 代數。根據可測函數的定義，我們需要在 ? 上構造 σ-代數? ，使得?中每個元素的原像都是E中的一個事件。但是，我們不能為 ? 中的每個元素分配非零概率因為集合的基數是無窮大，即它是不可數無限集合。任何為集合中的每個元素分配概率的嘗試都會導致 σ-代數?的概率為無窮大——這是一個矛盾，因為任何事件的概率都不能大于 1。

????????為了避免這個問題，我們轉向Borel σ-代數。這本身就是一個廣泛深入的話題，需要大量的拓撲知識，因此我們不會在本文中深入探討。但直觀上，Borel σ 代數處理的是實線上的所有區間，而不是實線本身。也就是說，實線上的區間(x,y)是 ? 的一個元素，因此在X下具有可測量的原像。并且，我們分配所有長度為零的區間，即僅包含一個實數的單例集，概率為0。也就是說，分配給任何特定實數的概率為零。然而，分配給實數區間的概率可以是非零的。

????????現在，我們如何計算 ? 中區間原像的測度？大多數情況下，這是通過使用概率密度函數來實現的——概率密度函數是概率中熟悉的概念。這是通過以下方式定義的：

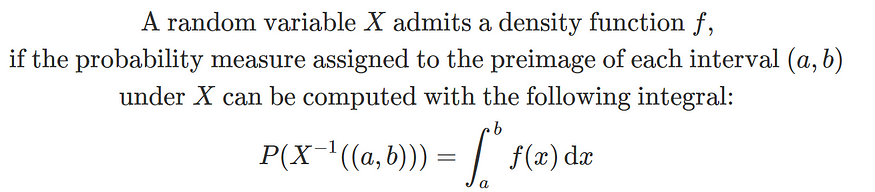
????????通常，LHS 表示為P(a < X < b)。

????????至此，我們現在統一了離散隨機變量和連續隨機變量的概念。希望這為概率論這個反直覺的怪物提供了一些令人滿意的直覺。而且，我應該說，測度論不僅僅用于統一這些概念。事實上，通過以這種方式定義隨機變量，我們現在已經配備了處理非數字結果（即向量、集合和函數）的隨機變量所需的機制。

????????本三部曲的最后一篇文章將探討如何使用測度論來理解數學期望。

????????感謝您的閱讀，祝您度過愉快的一天！