數據結構與算法（六）分支限界法（Java）

- 一、簡介
- - 1.1 定義
  - 1.2 知識回顧
  - 1.3 兩種解空間樹
  - 1.4 三種分支限界法
  - 1.5 回溯法與分支線定法對比
  - 1.6 使用步驟
- 二、經典示例：0-1背包問題
- - 2.1 題目
  - 2.2 分析
  - - 1）暴力枚舉
    - 2）分支限界法
  - 2.3 代碼實現
  - - 1）實現廣度優先策略遍歷
    - 2）實現限界函數來剪枝

一、簡介

1.1 定義

分支限界法 是使用 廣度優先策略，依次生成 擴展節點 上的所有分支。就是 把問題的可行解展開，再由各個分支尋找最佳解。

分支限界法 與 回溯法 類似，都是 遞歸 + 剪枝，區別在于回溯法使用的是深度優先策略，而分支限界法使用的是廣度優先策略。

1.2 知識回顧

擴展結點： 一個 正在生成兒子 的結點，稱為擴展結點。
活結點： 一個 自身已生成但其兒子還沒有全部生成 的結點，稱為活結點。
死結點： 一個 所有兒子已經全部生成 的結點，稱為死結點。

深度優先策略：

如果對一個擴展結點 R，一旦生成了它的一個兒子 C，就把 C 當作新的擴展結點。
在完成對子樹 C（以 C 為根的子樹）的窮盡搜索之后，將 R 重新變成擴展結點，繼續生成 R 的下一個兒子（如果存在）。

廣度優先策略：

在一個擴展結點變成死結點之前，它一直是擴展結點。

剪枝函數：

剪枝函數：當某個頂點沒有希望，則其所在的樹枝可以減去。

剪枝函數一般有兩種：

約束函數： 剪去不滿足約束條件的路徑。
限界函數： 減去不能得到最優解的路徑。

1.3 兩種解空間樹

子集樹（Subset Trees）：

當所給問題是 從 n 個元素的集合中找出滿足某種性質的子集 時，相應的解空間樹稱為 子集樹。

若 Sn 表示 n 結點子樹的數量，在子集樹中，|S0| = |S1| = ... = |Sn-1| = c，即每個結點有相同數目的子樹，通常情況下 c = 2，所以子樹中共有 2^n 個葉子結點。因此，遍歷子集樹的時間復雜度為 O(2^n)。

排列樹（Permutation Trees）：

當所給問題是 確定 n 個元素滿足某種性質的排列 時，相應的解空間樹稱為排列樹。

若 Sn 表示 n 結點子樹的數量，在排列樹中，通常情況下 |S0| = n, |S1| = n-1, ..., |Sn-1| = 1。所以，排列樹中共有 n! 個葉子結點。因此，遍歷排列樹的時間復雜度為 O(n!)。

1.4 三種分支限界法

不同于回溯法，在分支限界法中，每一個活結點只有一次機會成為擴展結點。活結點一旦成為擴展結點，就一次性產生其所有兒子結點，通過 剪枝函數 將導致不可行解或非最優解的兒子結點舍棄，其余 兒子結點被加入活結點表中。

然后，從 活結點表 中取下一結點成為當前擴展結點，并重復上述結點擴展過程。這個 過程一直持續到找到所需解或活結點表為空為止。

根據活結點表的形成方式不同分為 三種分支限界法：

FIFO分支限界法：活結點表是隊列，按照隊列先進先出（FIFO）原則選取下一個結點為擴展結點。
LIFO分支限界法：活結點表是堆棧，按照堆棧先今后出（LIFO）原則選取下一個結點為擴展結點。
LC分支限界法：活結點是 優先權隊列（Low Cost），按照優先隊列中規定的優先權選取具有最高優先級的活結點成為新的擴展結點。
- 結點優先權： 在其分支下搜索一個答案狀態需要花費的代價越小，優先級越高。

1.5 回溯法與分支線定法對比

算法名稱	對解空間樹的搜索方式	存儲結點的常用數據結構	結點存儲特性	求解目標	空間復雜度
`回溯法`	深度優先搜索（DFS）	遞歸；非遞歸時使用堆棧	活結點的所有可行子結點被遍歷后才被從棧中彈出（結點可能多次成為擴展結點）。	找出解空間樹中滿足約束條件的所有解。	子集樹：`O(n)` 排列樹：`O(n)`
`分支限界法`	廣度優先搜索（BFS）最小消耗優先搜索（LC）	隊列；堆棧、優先隊列	每個活結點只有一次成為擴展結點的機會。	找出滿足約束條件的一個解，或在滿足約束條件的解中找出某種意義下的最優解。	子集樹：`O(2^n)` 排列樹：`O(n!)`

1.6 使用步驟

首先 確定一個合理的限界函數，并 根據限界函數確定目標函數的界；
然后 按照廣度優先策略搜索問題的解空間樹；
在擴展結點處，生成所有兒子結點，估算所有兒子結點對目標函數的可能取值，舍棄不可能通向最優解的結點（剪枝），將其余結點加入到活結點表（隊列/棧）中；
在當前活結點表中，依據相應的分支線定法（FIFO、LIFO、LC），從當前活結點表中選擇一個結點作為擴展結點；
重復 4~3 步，直到找到所需的解或活結點表為空。

二、經典示例：0-1背包問題

2.1 題目

假定有N=4件商品，分別用A、B、C、D表示。每件商品的重量分別為 3kg、2kg、5kg和4kg，對應的價值分別為 66元、40元、95元和40元。現有一個背包，可以容納的總重量位 9kg，問：如何挑選商品，使得背包里商品的 總價值最大？

2.2 分析

0-1背包問題，實際上就是排列組合的問題。

1）暴力枚舉

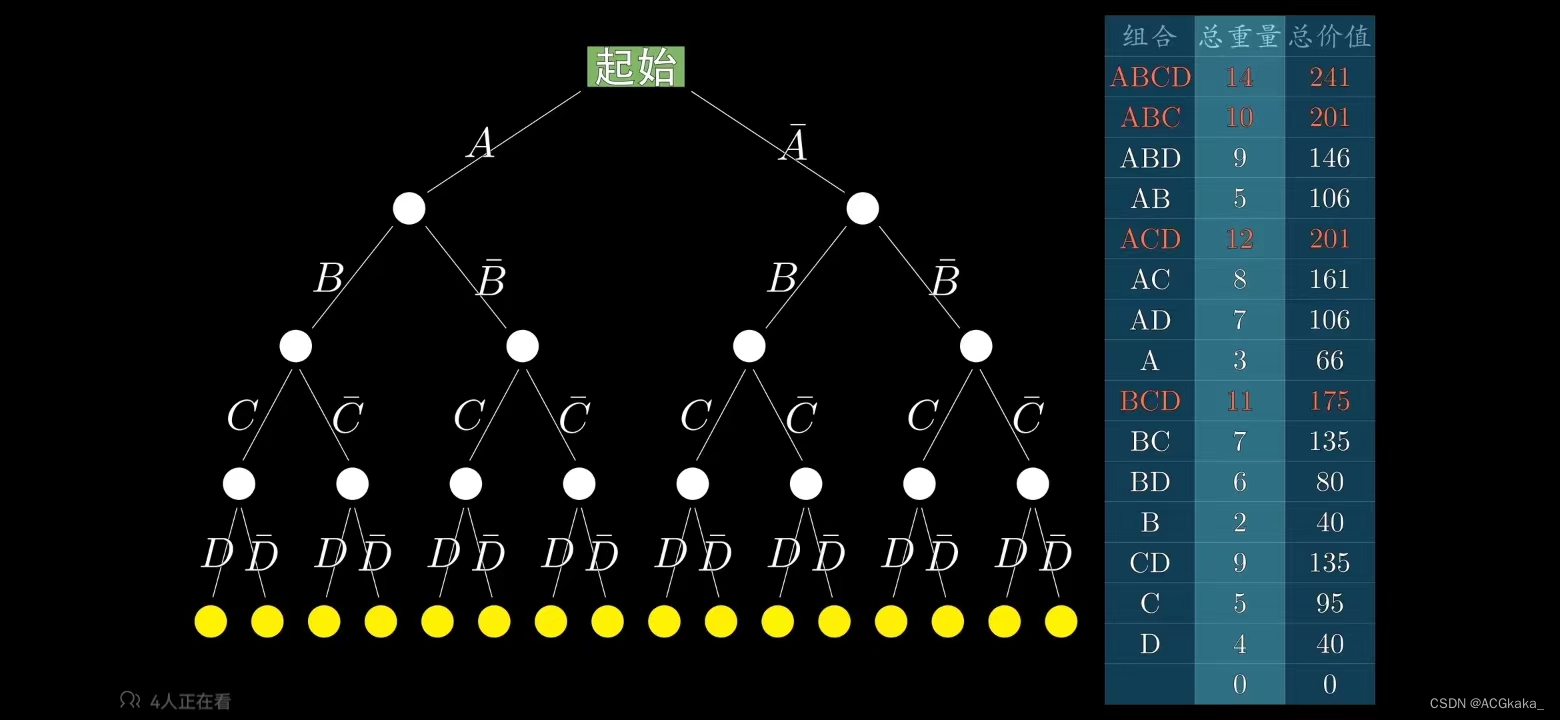
假如我們用A表示物品A存在；A（上劃線）表示物品A不存在。暴力枚舉所有可能的情況如下：

最優解： A 物品+ C 物品 = 161 價值

在這里插入圖片描述

2）分支限界法

首先根據 價值/重量 進行從大到小進行排序，排序結果如下：

重量：3，價值：66，每份重量價值：22；
重量：2，價值：40，每份重量價值：20；
重量：5，價值：95，每份重量價值：19；
重量：4，價值：40，每份重量價值：10；

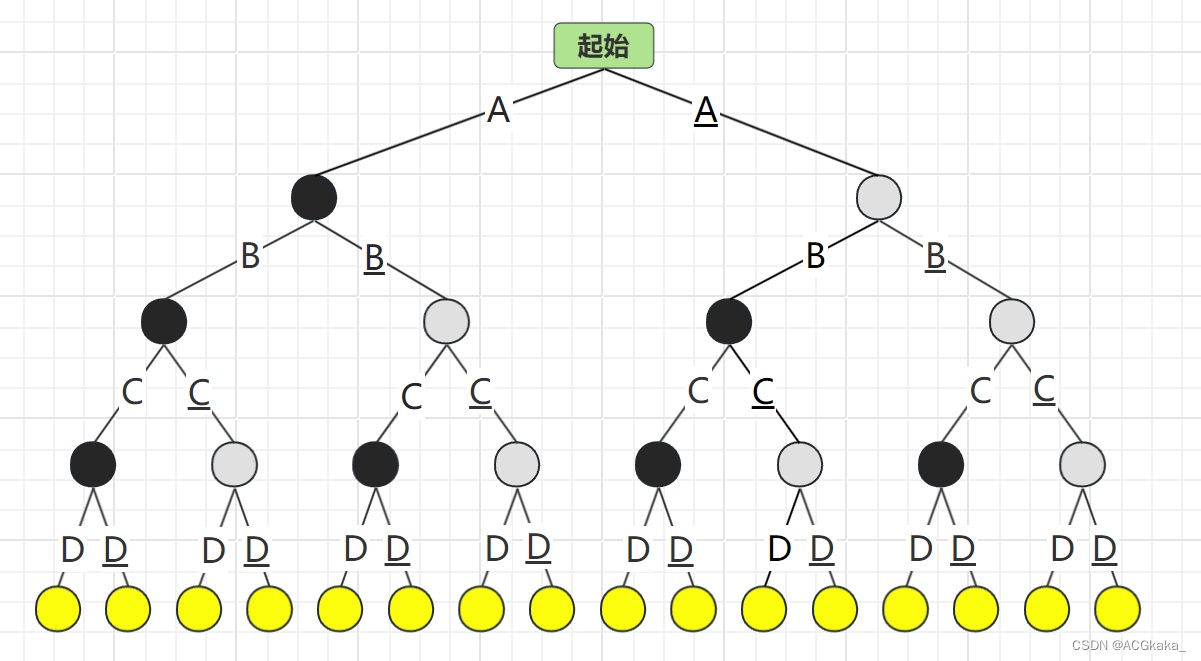
假如我們用A表示物品A存在；A（下劃線）表示物品A不存在。解空間樹 如下：

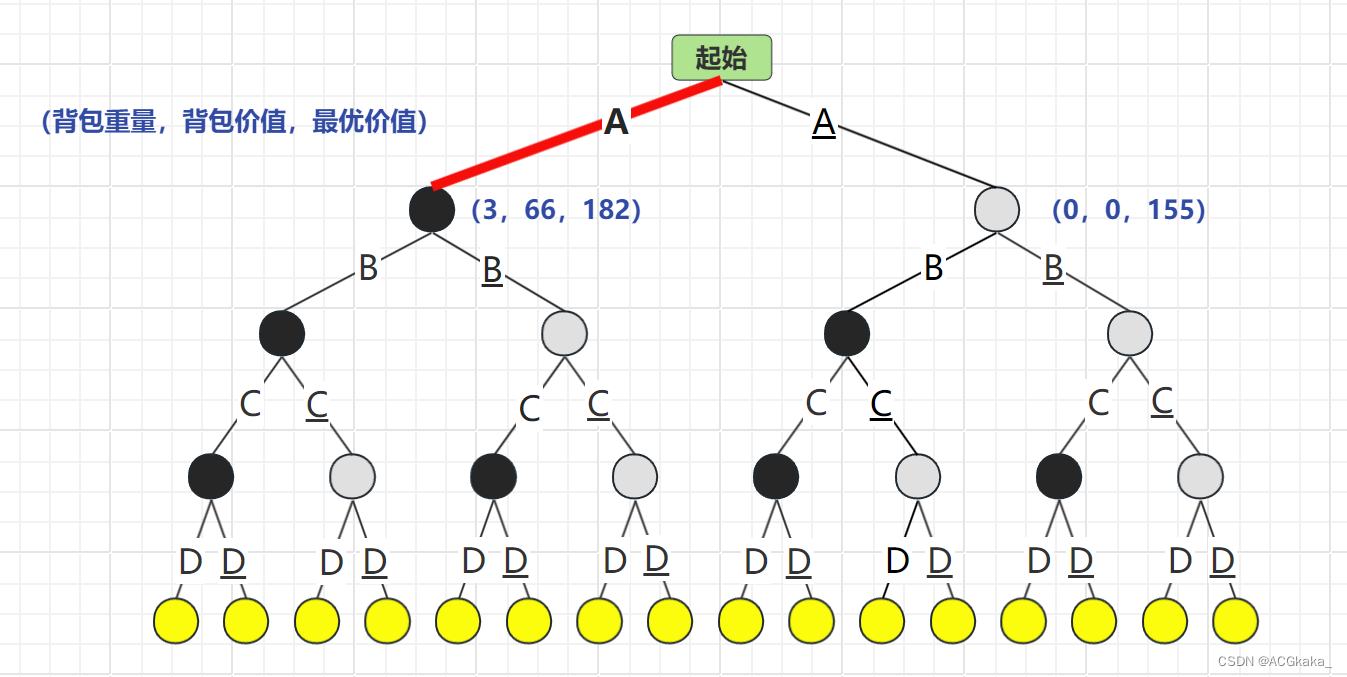
在這里插入圖片描述

首先根據 A 物品的存在情況進行計算，A存在時最優價值為182，A不存在時最優價值為155。選擇 最優價值更高的情況：A結點。

物品列表：A

背包價值：66

最優隊列： A（182）> A（155）

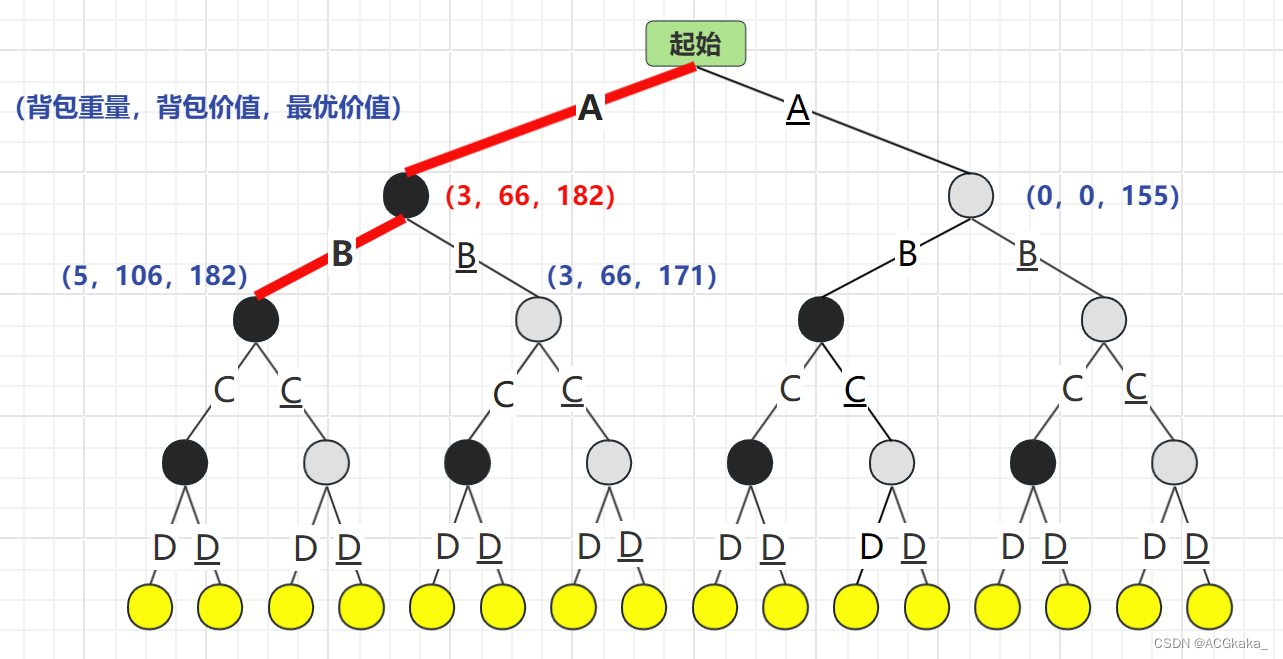
在這里插入圖片描述

彈出 A 結點，再根據 B 物品的存在情況進行計算，B存在時最優價值為182，B不存在時最優價值為171。選擇 最優價值更高的情況：B結點。

物品列表：A、B

背包價值：106

最優隊列： B（182）> B（171）> A（155）

在這里插入圖片描述

彈出 B 結點，再根據 C 物品的存在情況進行計算，C存在時超重×，C不存在時最優價值為146。選擇 最優價值更高的情況：B結點。

物品列表：A

背包價值：66

最優隊列： B（171）> A（155）> C（146）

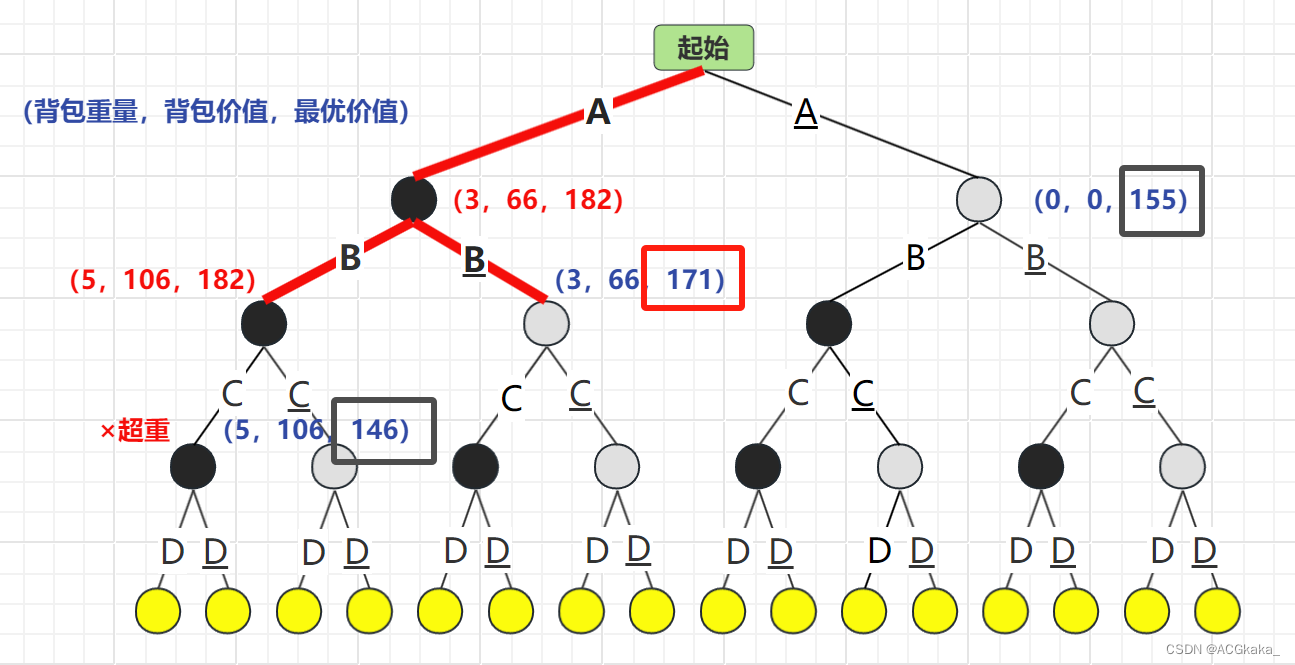
在這里插入圖片描述

彈出 B 結點，再根據 C 物品的存在情況進行計算，C存在時最優價值為171，C不存在時最優價值為106，由于 106 不大于已有最大價值 161，舍棄。選擇 最優價值更高的情況：C結點。

物品列表：A、C

背包價值：161

最優隊列： C（171）> A（155）> C（146）

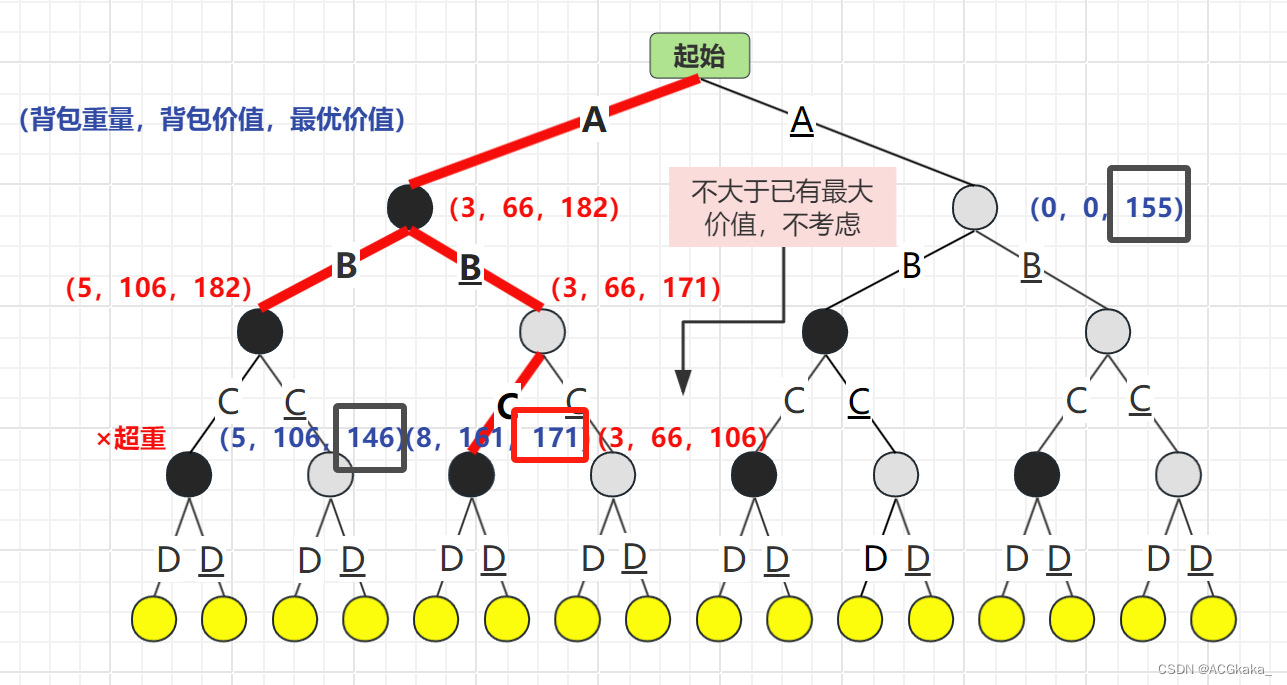
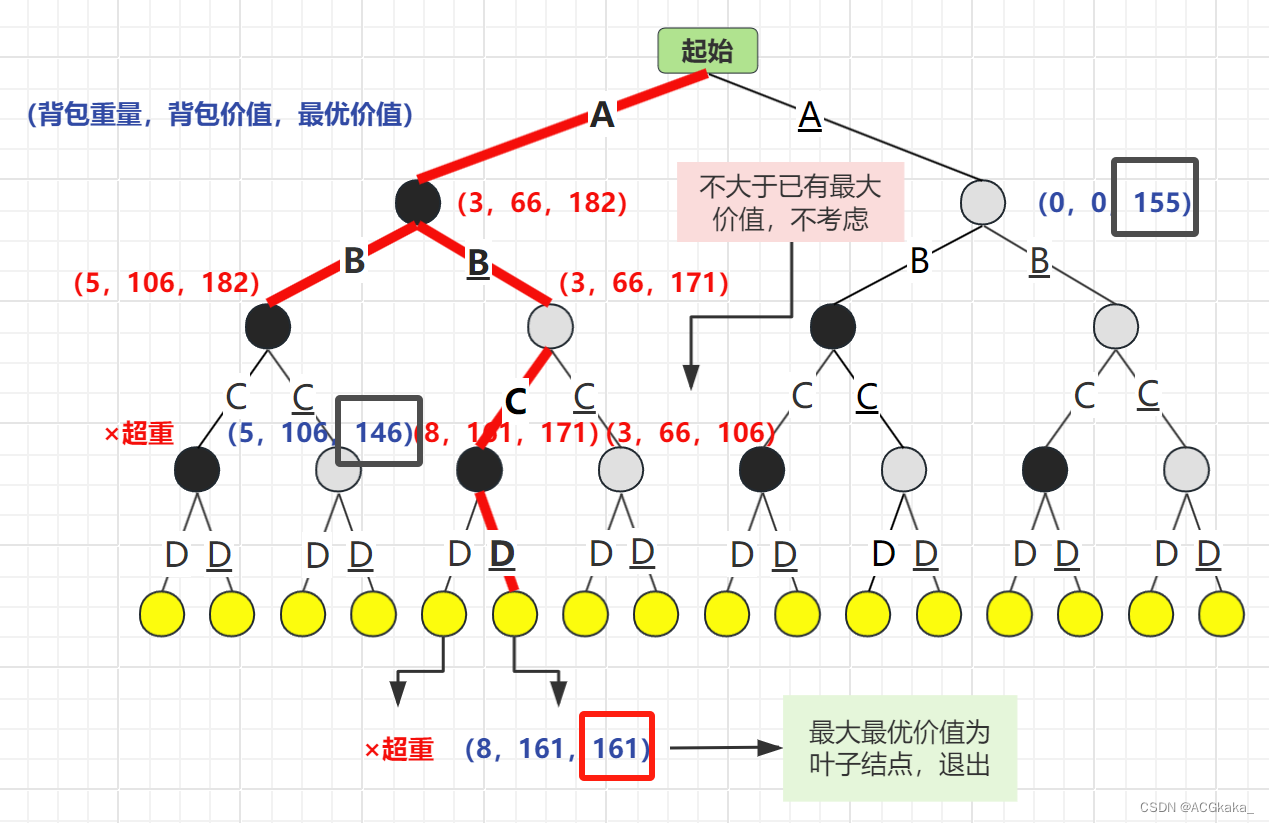
在這里插入圖片描述

彈出 C 結點，再根據 D 物品的存在情況進行計算，D存在時超重×，D不存在時最優價值為161。由于此結點已為葉子結點，退出循環。

物品列表：A、C

背包價值：161

在這里插入圖片描述

2.3 代碼實現

為了方便理解，這里分兩步實現：

實現廣度優先策略遍歷；
實現限界函數來剪枝。

1）實現廣度優先策略遍歷

public static void main(String[] args) {Solution solution = new Solution();int[][] arr1 = {{3,66},{2,40},{5,95},{4,40}};long start1 = System.currentTimeMillis();long start2 = System.nanoTime();// 執行程序int result = solution.knapsack(arr1, 9);long end1 = System.currentTimeMillis();long end2 = System.nanoTime();System.out.println(result);System.out.println("耗時：" + (end1 - start1) + " ms，" + (end2 - start2) + " ns");
}public int knapsack(int[][] nums, int capacity) {Node rootNode = new Node(0, 0, 0);Queue<Node> queue = new ArrayDeque<>();queue.add(rootNode);int maxValue = 0;while (!queue.isEmpty()) {Node node = queue.poll();if (node.index >= nums.length) {break;}// 左節點：放入背包if (node.bagWeight + nums[node.index][0] <= capacity) {Node newLeftNode = new Node(node.index + 1, node.bagWeight + nums[node.index][0], node.bagValue + nums[node.index][1]);queue.add(newLeftNode);maxValue = Math.max(maxValue, newLeftNode.bagValue);}// 右節點：不放入背包Node newRightNode = new Node(node.index + 1, node.bagWeight, node.bagValue);queue.add(newRightNode);}return maxValue;
}static class Node {/*** 索引（第幾個物品）*/private int index;/*** 背包容量*/private int bagWeight;/*** 背包價值*/private int bagValue;public Node(int index, int bagWeight, int bagValue) {this.index = index;this.bagWeight = bagWeight;this.bagValue = bagValue;}
}

2）實現限界函數來剪枝

public static void main(String[] args) {Solution solution = new Solution();int[][] arr1 = {{3,66},{2,40},{5,95},{4,40}};long start1 = System.currentTimeMillis();long start2 = System.nanoTime();// 執行程序int result = solution.knapsack(arr1, 9);long end1 = System.currentTimeMillis();long end2 = System.nanoTime();System.out.println(result);System.out.println("耗時：" + (end1 - start1) + " ms，" + (end2 - start2) + " ns");
}public int knapsack(int[][] nums, int capacity) {// 由于使用了貪心算法，需要先進行排序Arrays.sort(nums, Comparator.comparingDouble(o -> -1.0 * o[1] / o[0]));Node rootNode = new Node(0, 0, 0);// 優先隊列（貪心算法，按照最優價值排序）PriorityQueue<Node> queue = new PriorityQueue<>();queue.add(rootNode);int maxValue = 0;// 遍歷，直到最大最優價值為某一葉子結點while (queue.size() > 0 && queue.peek().index < nums.length) {Node node = queue.poll();// 左節點：放入背包Node newLeftNode = new Node(node.index + 1, node.bagWeight + nums[node.index][0], node.bagValue + nums[node.index][1]);int newLeftUpBound = newLeftNode.getUpBound(nums, capacity);if (newLeftUpBound >= maxValue && newLeftNode.bagWeight <= capacity) {queue.add(newLeftNode);maxValue = Math.max(maxValue, newLeftNode.bagValue);}// 右節點：不放入背包Node newRightNode = new Node(node.index + 1, node.bagWeight, node.bagValue);int newRightUpBound = newRightNode.getUpBound(nums, capacity);if (newRightUpBound >= maxValue) {queue.add(newRightNode);}}return maxValue;
}static class Node implements Comparable<Node> {/*** 索引（例：第 1個物品索引為 1）*/private final int index;/*** 背包容量*/private final int bagWeight;/*** 背包價值*/private final int bagValue;/*** 背包最優價值（上界）*/private int upBound;public Node(int index, int bagWeight, int bagValue) {this.index = index;this.bagWeight = bagWeight;this.bagValue = bagValue;}public int getUpBound(int[][] nums, int capacity) {if (this.upBound > 0) {return this.upBound;}int newUpBound = this.bagValue;int bagLeft = capacity - bagWeight;int i = this.index;while (i < nums.length && bagLeft - nums[i][0] >= 0) {bagLeft -= nums[i][0];newUpBound += nums[i][1];i++;}// 背包未滿，切割后放入if (i < nums.length) {newUpBound += 1.0 * bagLeft / nums[i][0] * nums[i][1];}return this.upBound = newUpBound;}@Overridepublic int compareTo(Node o) {// 倒敘return o.upBound - this.upBound;}
}