1.優先級隊列

? ? ? ? 由前文隊列queue可知，隊列是一種先進先出(FIFO)的數據結構，但有些情況下，操作的數據可能帶有優先級，一般出隊列時，可能需要優先級高的元素先出隊列，在此情況下，使用隊列queue顯然不合適，

????????同時在我們生活場景中也有類似于這中優先事情處理的情況，在醫院看病的時候大家都在排隊，突然有一個頭上插了一把刀的老爺爺也來排隊，這時候雖然大家都很急著去看病，但是出于老爺爺情況緊急，所以大家都會默認讓老爺爺優先去見醫生，而不是讓老爺爺按照一般的規則去老老實實的排隊；

? ? ? ? 考慮到隨時會遇到上述這種情況，數據結構應該提供兩個最基本的操作，一個是返回最高優先級對象，一個是添加新的對象。這種數據結構就是優先級隊列(Priority Queue)。

2.初識堆

????????JDK1.8中的PriorityQueue底層使用了堆這種數據結構，而堆實際就是在完全二叉樹的基礎上進行了一些調整。

2.1 堆的概念

????????如果有一個關鍵碼的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉樹的順序存儲方式存儲 在一 個一維數組中，并滿足：Ki = K2i+1 且 Ki >= K2i+2) i = 0，1，2…，則稱為 小堆(或大 堆)。將根節點最大的堆叫做最大堆或大根堆，根節點最小的堆叫做最小堆或小根堆。

堆的性質

• 堆中某個節點的值總是不大于或不小于其父節點的值；

• 堆總是一棵完全二叉樹。

2.1.1 小根堆?

? ? ? ? ? ? ? ? ? ? ? ?

? ? ? ? 如上圖小根堆的邏輯結構所示，在一顆大的完全二叉樹中的小二叉樹中，該小二叉樹的根節點遠遠小于該樹左右子節點，且這時候不考慮左右子節點的數值哪個大；

2.1.2 大根堆

? ? ? ? ? ? ? ??

???????? 如上圖大根堆的邏輯結構所示，給一顆大的完全二叉樹中的小二叉樹中，該小二叉樹的根節點遠遠大于于該樹左右子節點，且這時候不考慮左右子節點的數值哪個大；

2.2 堆的存儲方式

????????從堆的概念可知，堆是一棵完全二叉樹，因此可以層序的規則采用順序的方式來高效存儲，如下圖所示堆的存儲圖解；（堆是將一個一維數組中的數據按照層序遍歷的規則將這些數據存儲到一個完全二叉樹里的完全二叉樹）

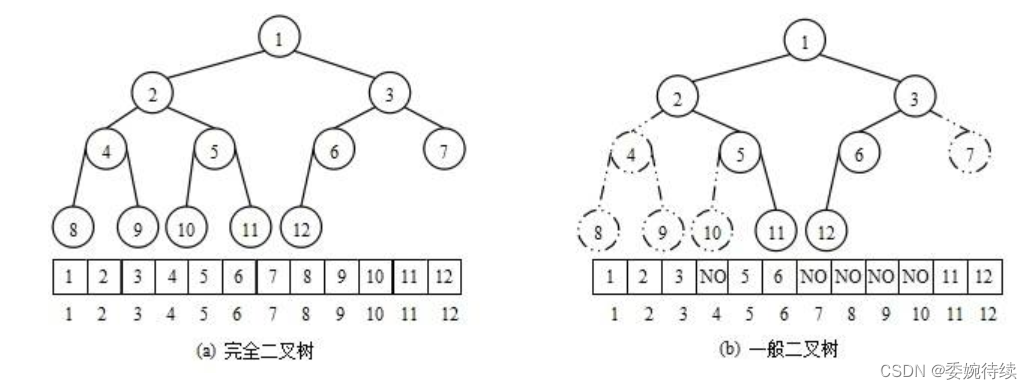
????????注意：由該圖中的邏輯結構和存儲結構可知，對于非完全二叉樹，則不適合使用順序方式進行存儲，因為為了通過一維存儲結構能夠還原二叉樹，一維存儲空間中必須要存儲空節點，就會導致該存儲空間利用率比較低。

???????? 將元素存儲到數組中后，可以根據本主初識二叉樹章節的性質5對樹進行還原。

????????假設i為節點在數組中的下標，則有：

????????如果i為0，則i表示的節點為根節點，否則i節點的雙親節點為 (i - 1)/2

????????如果2 * i + 1 小于節點個數，則節點i的左孩子下標為2 * i + 1，否則沒有左孩子

????????如果2 * i + 2 小于節點個數，則節點i的右孩子下標為2 * i + 2，否則沒有右孩子?

2.3 堆的創建（小根堆）

2.3.1 堆向下調整

? ? ? ? 思考：

????????對于集合{ 27,15,19,18,28,34,65,49,25,37 }中的數據，如何將其創建成堆，首先按照堆的規則將以上數劇放入到完全二叉樹里面，如下圖所示：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

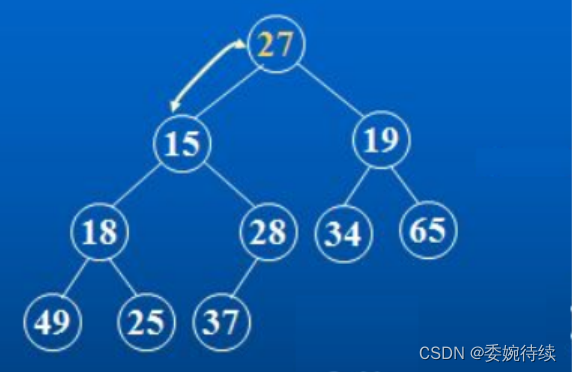
????????仔細觀察上圖后發現：當前根節點27的左右子樹已經完全滿足堆的性質，因此只需將根節點向下調整好即可。

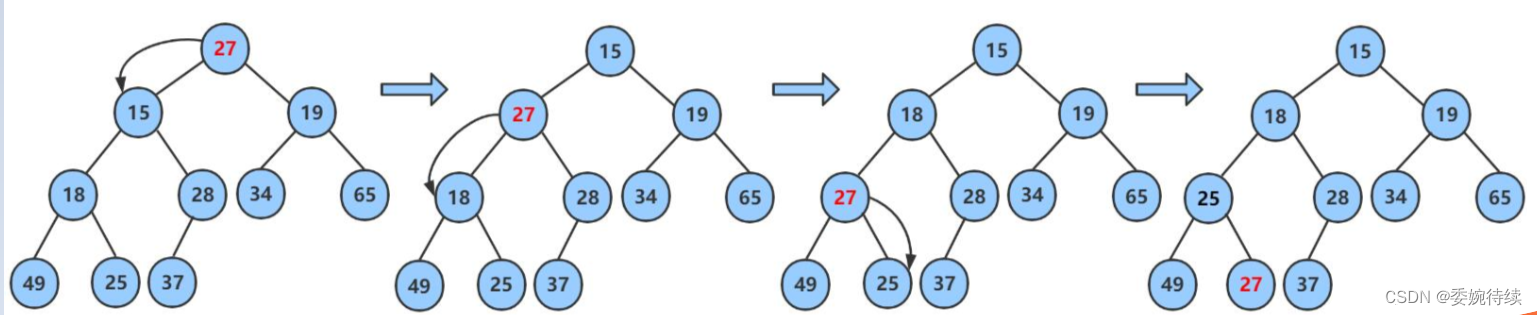
? ? ? ? 調整過程如下：

1. 讓parent標記需要調整的節點，child標記parent的左孩子(注意：parent如果有孩子一定先是有左孩子)

2. 如果parent的左孩子存在，即:child < size， 進行以下操作，直到parent的左孩子不存在? ? ? ? ?2.1parent右孩子是否存在，存在找到左右孩子中最小的孩子，讓child進行標

? ? ?2.2將parent與較小的孩子child比較，如果：

? ? ? ? ? ? ? ? 2.2.1 parent小于較小的孩子child，調整結束

? ? ? ? ? ? ? ? 2.2.2 否則：交換parent與較小的孩子child，交換完成之后，parent中大的元素向下移動，可能導致子樹不滿足對的性質，因此需要繼續向下調整，即parent = child；child = parent*2+1（左子樹）; 然后繼續2

? ? ? ? 詳細調整圖解如下圖所示：

2.3.2 小根堆代碼實現

package com.bit.demo1;public class MySmallHeap {public void shiftDown(int[] array, int parent) {//child和parent時數組存儲的節點的索引// child先標記parent的左孩子，因為parent可能右左沒有右int child = 2*parent + 1;int size = array.length;//所有節點的數目while(child < size ) {//主要保證當前訪問到的child都在所有節點的范圍內，是有效的//child+1是二叉樹的最后一個節點// 如果右孩子存在，找到左右孩子中較小的孩子,用child進行標記if(child + 1 < size) {if(array[child + 1] < array[child]) {child = child + 1;}}// 如果最小的孩子比其父親還小，說明該結構沒有滿足堆的特性，進行交換if(array[child] < array[parent]) {int tmp = array[parent];array[parent] = array[child];array[child] = tmp;} else {//滿足就退出循環break;}// parent中大的元素往下移動，可能會造成子樹不滿足堆的性質，因此需要繼續向下調整parent = child;child = 2*parent + 1;}}}

2.3.3?小根堆代碼測試

 public static void main(String[] args) {MySmallHeap mySmallHeap = new MySmallHeap();int[] array = {27,15,19,18,28,34,65,49,25,37};System.out.println("調整前：");for(int i = 0; i < array.length ; i++) {System.out.print(array[i] + " ");}for(int parent = (array.length-2)/2 ; parent >= 0; parent --) {mySmallHeap.shiftDown(array, parent);}System.out.println();System.out.println("調整后：");for(int i = 0; i < array.length ; i++) {System.out.print(array[i] + " ");}System.out.println();}

? ? ? ? 關于最初的parent索引 ？

? ? ? ? 測試結果如下圖所示：

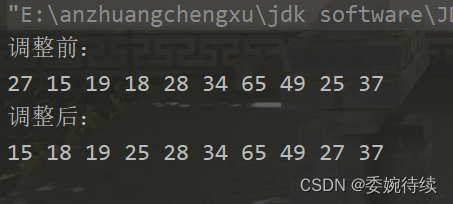
?????????注意：在調整以parent為根的二叉樹時，必須要滿足parent的左子樹和右子樹已經是堆了才可以向下調整。

????????最壞的情況即圖示的情況，從根一路比較到葉子，比較的次數為完全二叉樹的高度，即時間復雜度為

2.4 建堆的時間復雜度

2.4.1 建堆的步驟圖解

????????對于普通的序列{ 1,5,3,8,7,6 }，我們需要建立大堆，即根節點的左右子樹不滿足堆的特性，又該如何調整呢，其中里面的細節如下：

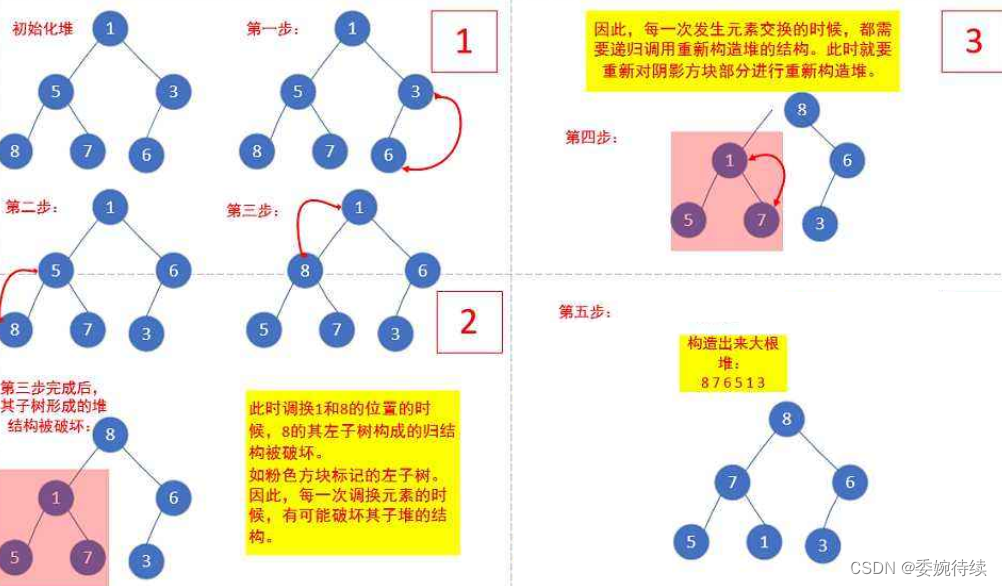
? ? ? ? 大概思路：

????????找倒數第一個非葉子節點（最右側的最小子樹根節點），從該節點位置開始往前進行按照根堆的規則運作，一直運作到根節點，這時候才確定根節點的數值；

? ? ? ? 因為為了根節點導致下面的不同子樹的結構都發生了變化，所以接下來確定索引為1的根節點的數字，這樣就需要重復上述的步驟；

? ? ? ? 就這樣重復上面兩個步驟，知道確定最右側最小子樹的根節點（索引為（arr.length-2）/2）的數值，我們的整體過程才算結束；

2.4.2 時間復雜度求解圖解

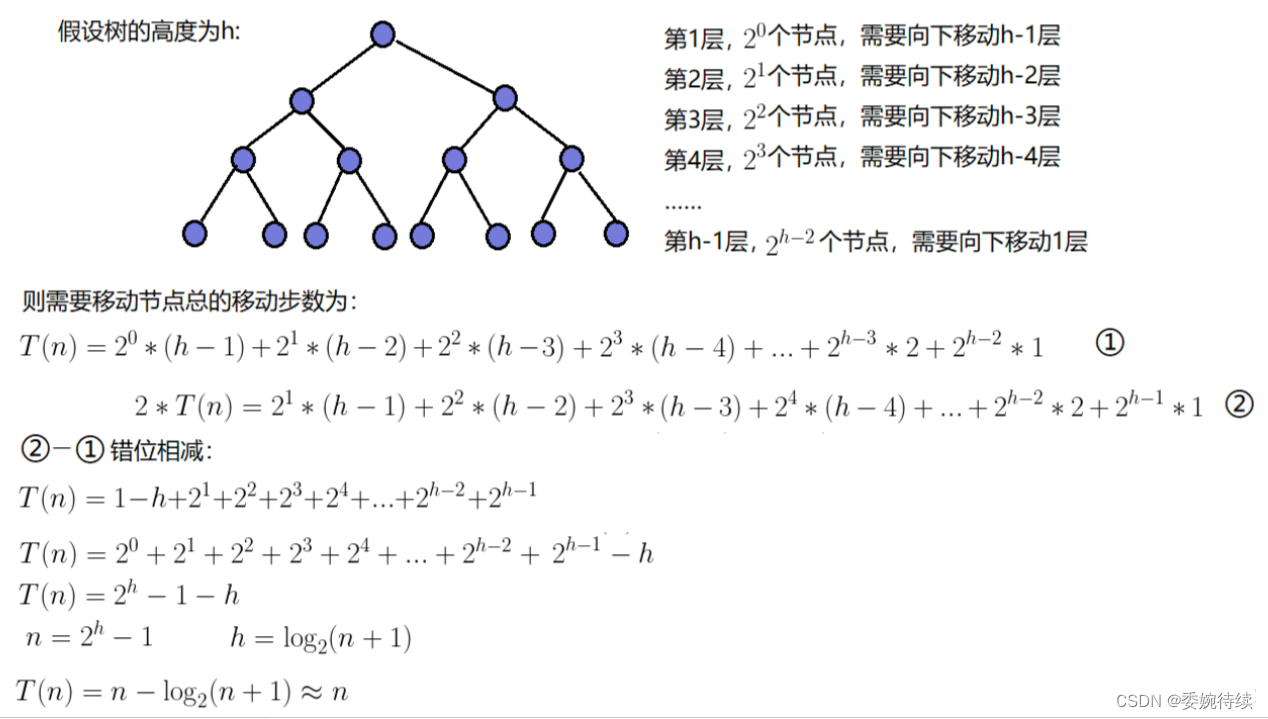
? ? ? ? 至此可得：建堆的時間復雜度為O(N)

ps：本次的內容就到這里了，如果喜歡的話就請一鍵三連哦！！！