有意向獲取代碼,請轉文末觀看代碼獲取方式~也可轉原文鏈接獲取~
1 基本定義
MODWT分解+FFT+HHT組合算法是一種綜合性的信號處理方法,它結合了經驗小波變換(Empirical Wavelet Transform,EWT)、快速傅里葉變換(Fast Fourier Transform,FFT)和希爾伯特黃變換(Hilbert-Huang Transform,HHT)的優點,具有較高的計算效率和準確性。
在MODWT分解+FFT+HHT組合算法中,首先使用MODWT對信號進行自適應分解,得到一系列本征模函數(Intrinsic Mode Functions,IMF);然后對每個IMF進行FFT計算其頻譜特征;最后使用HHT對每個IMF進行希爾伯特譜分析,得到信號的時頻分布和能量特征。
MODWT分解+FFT+HHT組合算法的具體步驟如下:
-
對輸入信號進行MODWT分解,得到一系列本征模函數(IMF。MODWT是一種自適應的信號分解方法,能夠將信號分解為一系列具有不同尺度的IMF,每個IMF都對應著信號中的某個特征尺度。
-
對每個IMF進行FFT計算,得到其頻譜特征。FFT是一種高效的計算離散傅里葉變換(DFT)的算法,能夠快速計算信號的頻譜。通過FFT,我們可以得到每個IMF在不同頻率下的貢獻。
-
對每個IMF進行希爾伯特黃變換(HHT),得到其時頻分布和能量特征。HHT是一種非線性、非穩定信號的處理方法,能夠得到信號的瞬時頻率和瞬時幅值。通過HHT,我們可以得到每個IMF在不同時刻的頻率和幅值信息。
通過以上步驟,MODWT 分解+FFT+HHT 組合算法能夠得到輸入信號在不同尺度、不同頻率和不同時刻下的特征信息,從而為信號的分析和處理提供了全面的信息。同時,該算法結合了自適應分解、頻譜分析和希爾伯特譜分析的優點,具有較高的計算效率和準確性。
除了在信號處理領域的應用,MODWT分解+FFT+HHT組合算法還可以應用于其他領域。例如,在圖像處理中,可以將圖像看作一個信號,對其執行MODWT分解+FFT+HHT組合算法來得到圖像的頻譜特征和邊緣信息。在語音處理中,可以使用該算法對語音信號進行分析,得到其頻譜特征和音調信息。
此外,MODWT分解+FFT+HHT組合算法還可以與其他方法結合使用,以進一步提高處理效果。例如,可以將MODWT分解與小波包變換(Wavelet Packet Transform,WPT)結合使用,得到更精細的信號分解結果;可以將FFT與短時傅里葉變換(Short-Time Fourier Transform,STFT)結合使用,得到信號在不同時間窗下的頻譜特征;可以將HHT與經驗模態分解(Empirical Mode Decomposition,EMD)結合使用,得到更準確的IMF。
總之,MODWT分解+FFT+HHT組合算法是一種綜合性的信號處理方法,具有廣泛的應用前景。通過對其深入研究和改進,可以為各個領域的研究和應用提供有力的支持。
2 出圖效果
附出圖效果如下:
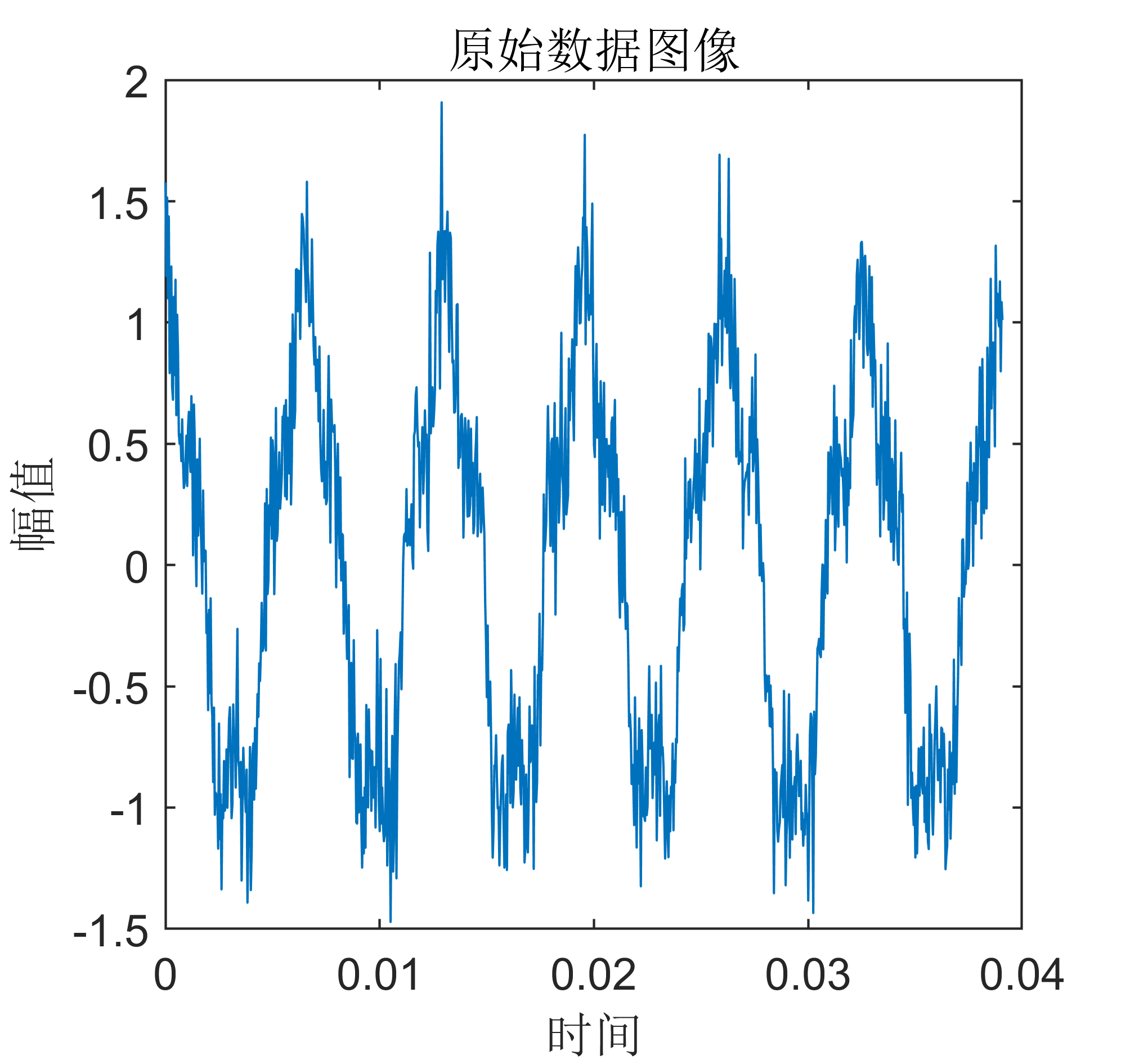
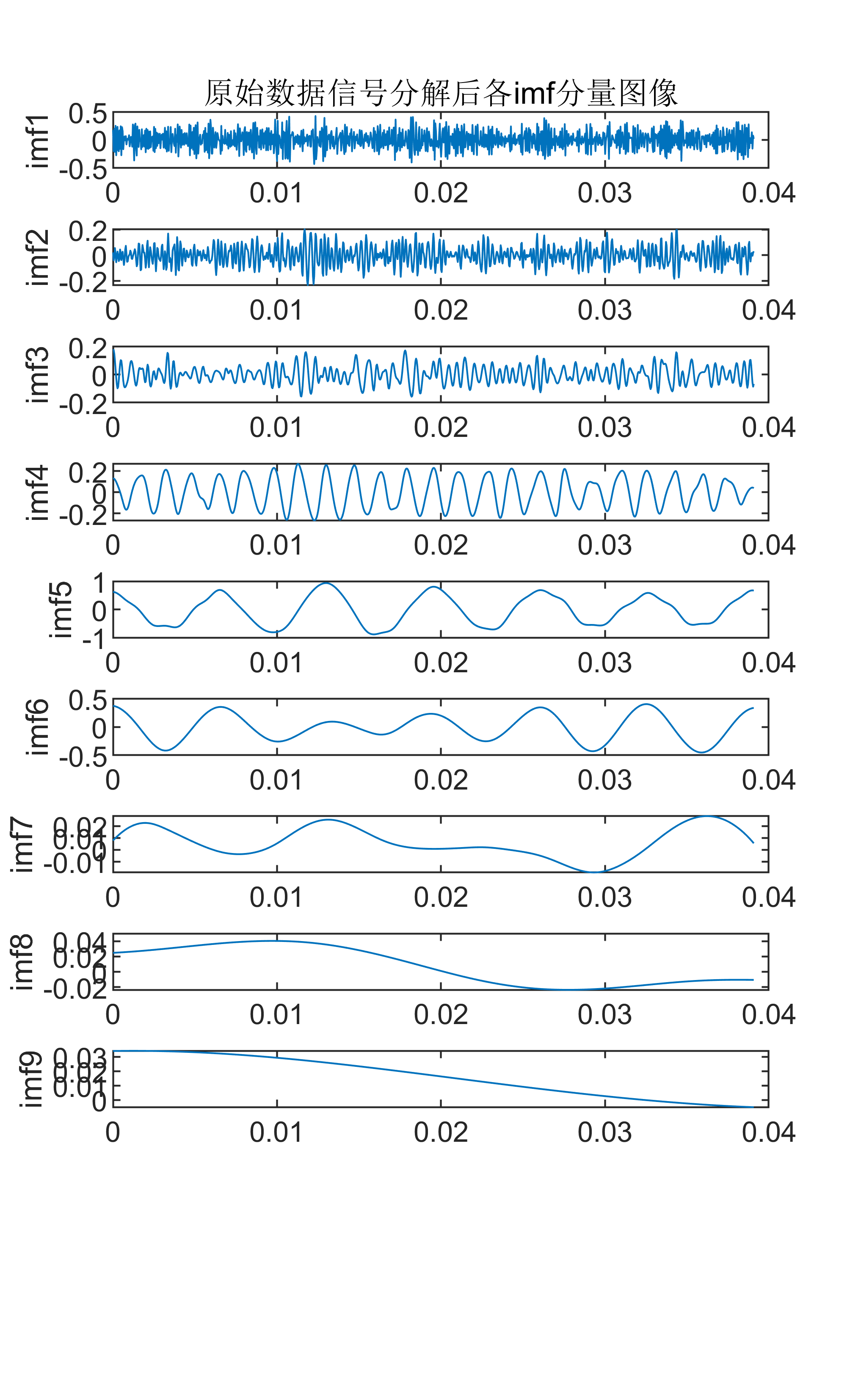
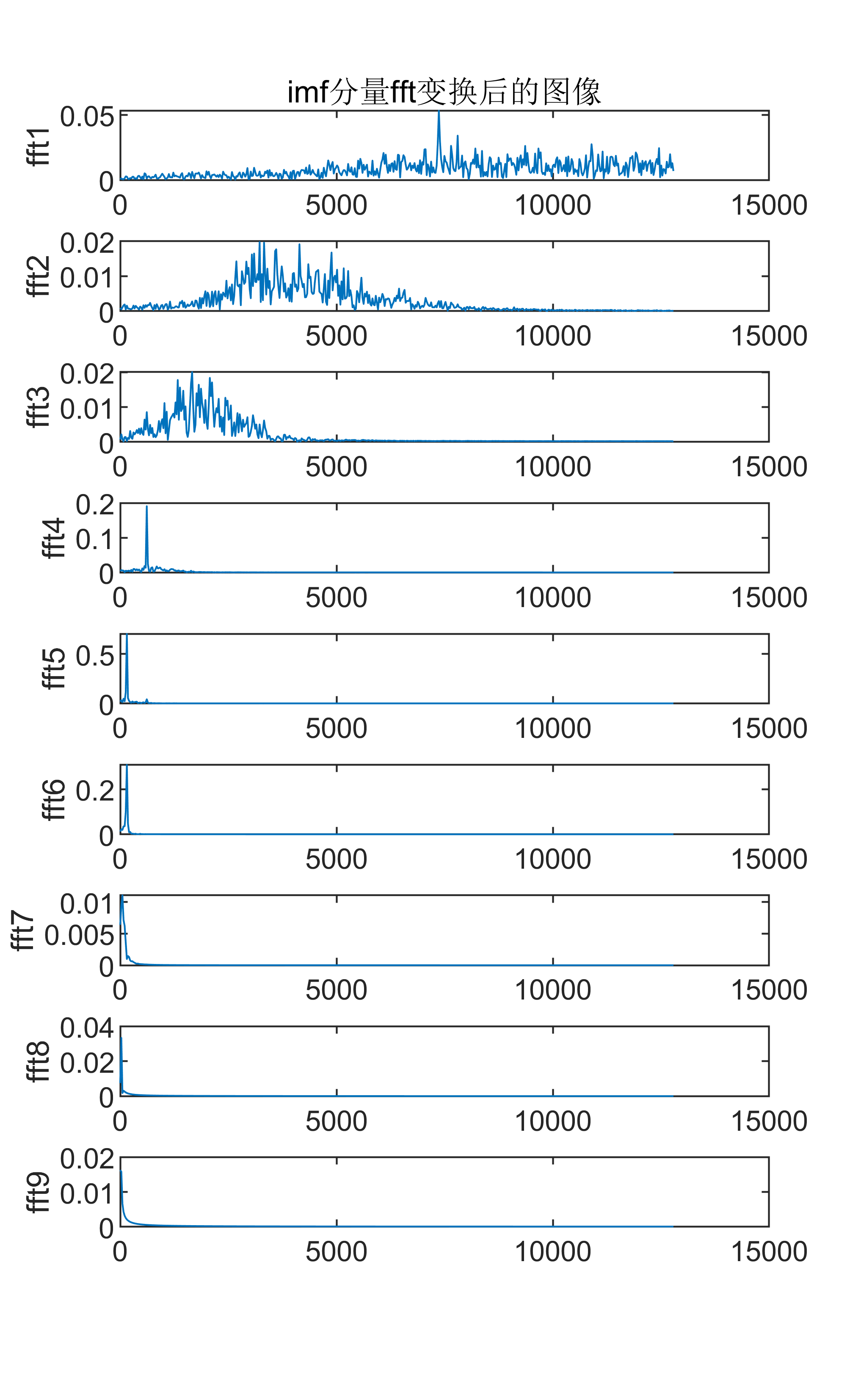
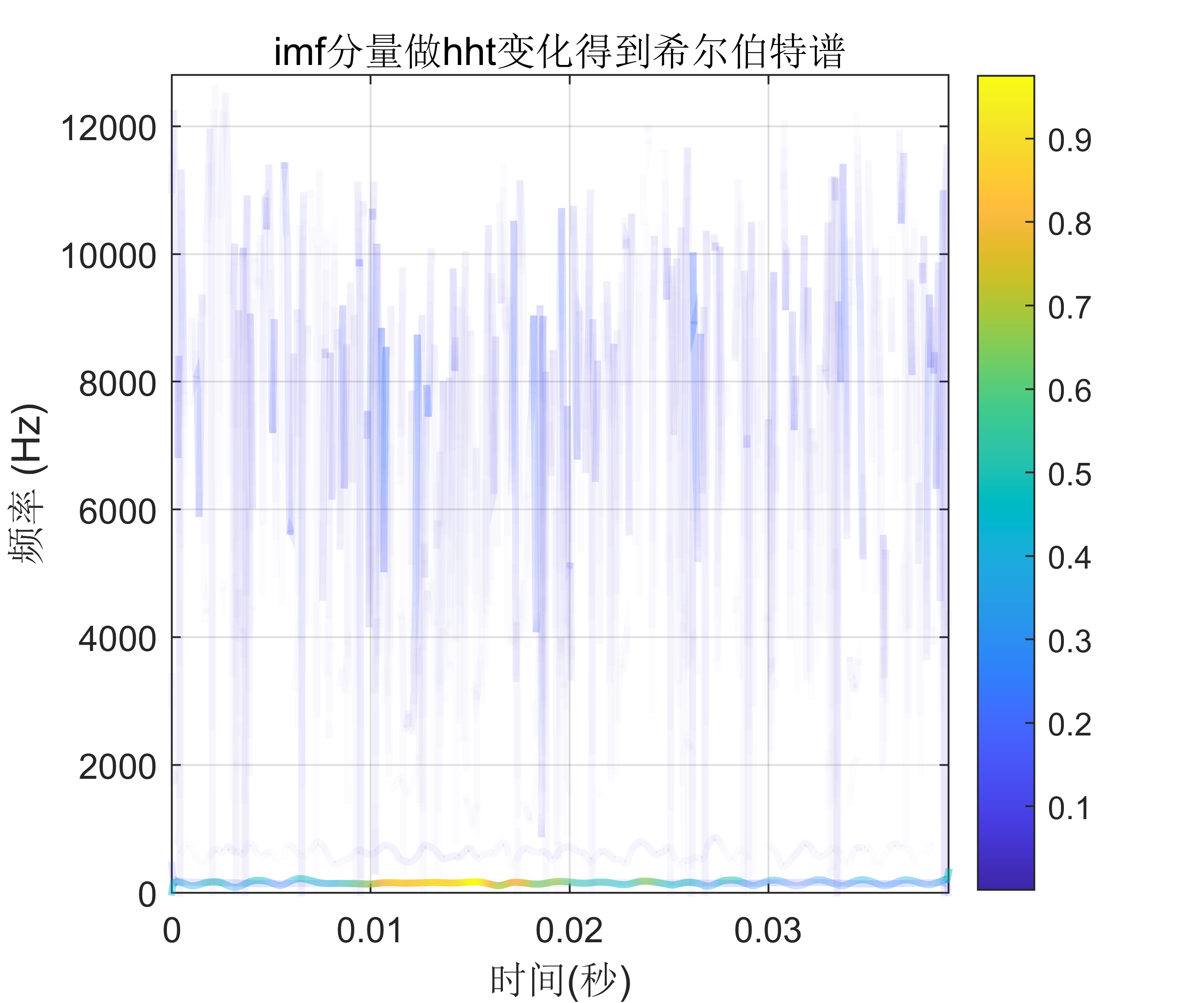
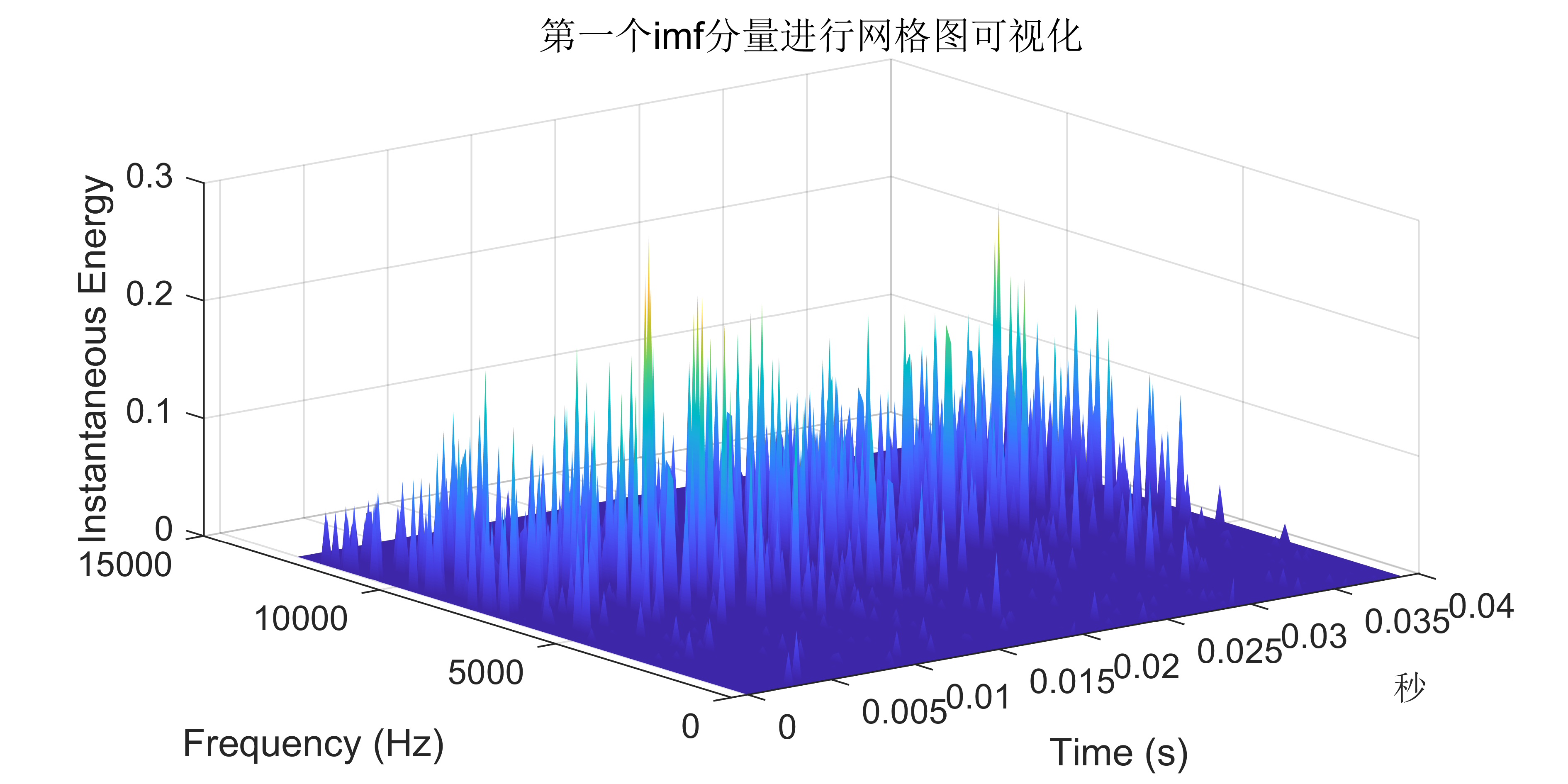
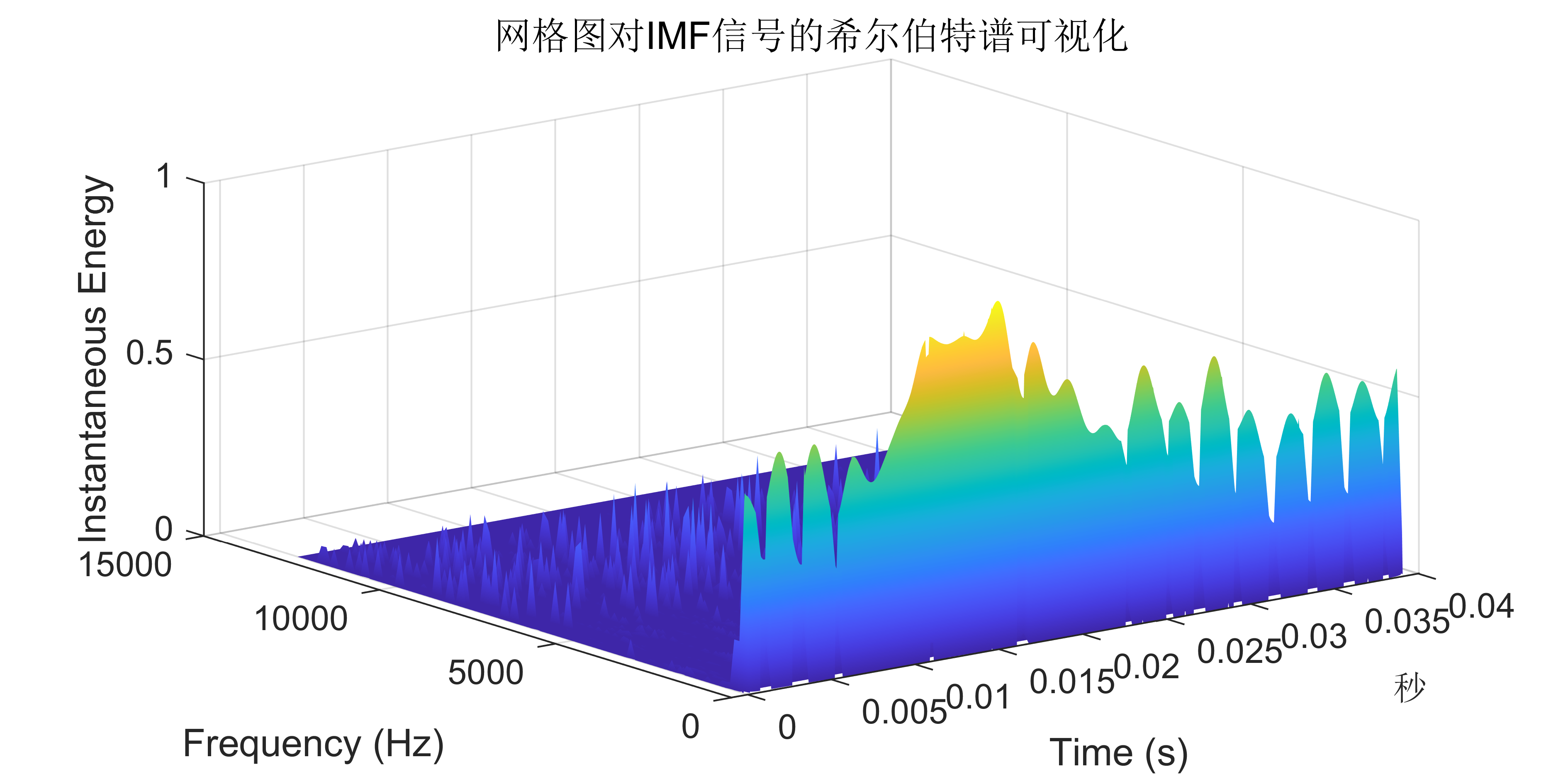
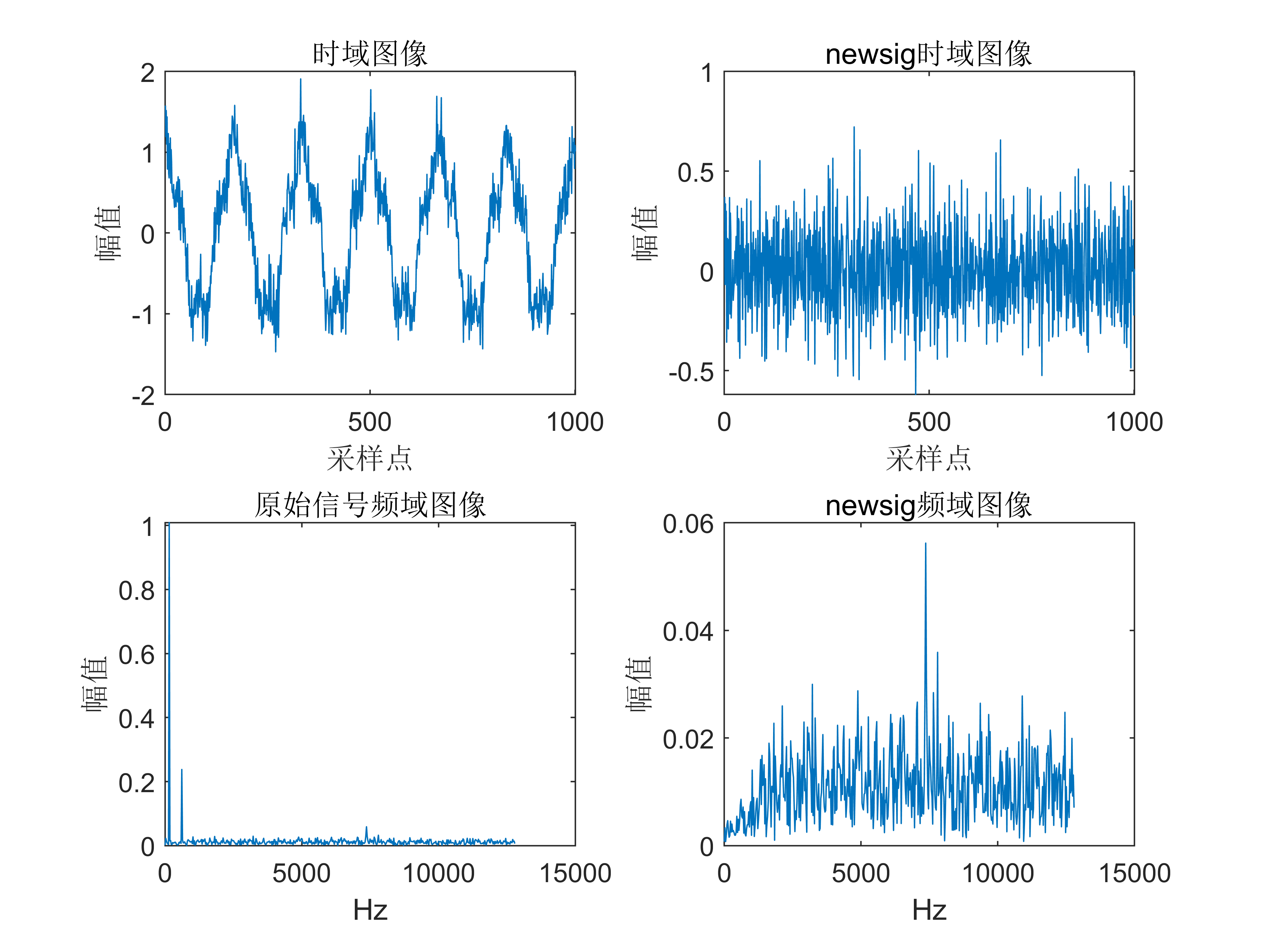
附視頻教程操作:
【MATLAB】MODWT分解+FFT+HHT組合算法




)



)






)



