目錄

解法：

官方解法：

方法一：深度優先搜索

復雜度分析

時間復雜度：

空間復雜度：

方法二：廣度優先搜索

復雜度分析

時間復雜度：

空間復雜度：

---

給你兩棵二叉樹的根節點?p?和?q?，編寫一個函數來檢驗這兩棵樹是否相同。

如果兩個樹在結構上相同，并且節點具有相同的值，則認為它們是相同的。

示例 1：

輸入：p = [1,2,3], q = [1,2,3]
輸出：true

示例 2：

輸入：p = [1,2], q = [1,null,2]
輸出：false

示例 3：

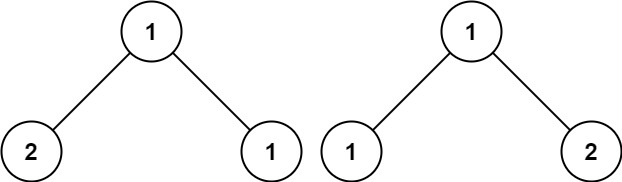
輸入：p = [1,2,1], q = [1,1,2]
輸出：false

提示：

• 兩棵樹上的節點數目都在范圍?[0, 100]?內
• -10^4?<= Node.val <= 10^4

解法：

用深度優先遍歷的方法將樹中的元素分別取出，用StringBuilder進行接收，然后用equals方法判斷是否相同。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {StringBuilder sb1 = new StringBuilder();StringBuilder sb2 = new StringBuilder();hasNextNode(p, sb1);hasNextNode(q, sb2);return sb1.toString().equals(sb2.toString());}public void hasNextNode(TreeNode root, StringBuilder sb) {if (root == null) {return;} else {sb.append(root.val).append("-");}if (root.left != null) {hasNextNode(root.left, sb);} else {sb.append("-");}if (root.right != null) {hasNextNode(root.right, sb);} else {sb.append("-");}}
}

---

---

官方解法：

方法一：深度優先搜索

如果兩個二叉樹都為空，則兩個二叉樹相同。如果兩個二叉樹中有且只有一個為空，則兩個二叉樹一定不相同。

如果兩個二叉樹都不為空，那么首先判斷它們的根節點的值是否相同，若不相同則兩個二叉樹一定不同，若相同，再分別判斷兩個二叉樹的左子樹是否相同以及右子樹是否相同。這是一個遞歸的過程，因此可以使用深度優先搜索，遞歸地判斷兩個二叉樹是否相同。

class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if (p == null && q == null) {return true;} else if (p == null || q == null) {return false;} else if (p.val != q.val) {return false;} else {return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);}}
}

復雜度分析

時間復雜度：

O(min?(m,n))，其中 m 和 n?分別是兩個二叉樹的節點數。對兩個二叉樹同時進行深度優先搜索，只有當兩個二叉樹中的對應節點都不為空時才會訪問到該節點，因此被訪問到的節點數不會超過較小的二叉樹的節點數。

空間復雜度：

O(min?(m,n))，其中 m 和 n 分別是兩個二叉樹的節點數。空間復雜度取決于遞歸調用的層數，遞歸調用的層數不會超過較小的二叉樹的最大高度，最壞情況下，二叉樹的高度等于節點數。

方法二：廣度優先搜索

也可以通過廣度優先搜索判斷兩個二叉樹是否相同。同樣首先判斷兩個二叉樹是否為空，如果兩個二叉樹都不為空，則從兩個二叉樹的根節點開始廣度優先搜索。

使用兩個隊列分別存儲兩個二叉樹的節點。初始時將兩個二叉樹的根節點分別加入兩個隊列。每次從兩個隊列各取出一個節點，進行如下比較操作。

1.比較兩個節點的值，如果兩個節點的值不相同則兩個二叉樹一定不同；

2.如果兩個節點的值相同，則判斷兩個節點的子節點是否為空，如果只有一個節點的左子節點為空，或者只有一個節點的右子節點為空，則兩個二叉樹的結構不同，因此兩個二叉樹一定不同；

3.如果兩個節點的子節點的結構相同，則將兩個節點的非空子節點分別加入兩個隊列，子節點加入隊列時需要注意順序，如果左右子節點都不為空，則先加入左子節點，后加入右子節點。

如果搜索結束時兩個隊列同時為空，則兩個二叉樹相同。如果只有一個隊列為空，則兩個二叉樹的結構不同，因此兩個二叉樹不同。

class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if (p == null && q == null) {return true;} else if (p == null || q == null) {return false;}Queue<TreeNode> queue1 = new LinkedList<TreeNode>();Queue<TreeNode> queue2 = new LinkedList<TreeNode>();queue1.offer(p);queue2.offer(q);while (!queue1.isEmpty() && !queue2.isEmpty()) {TreeNode node1 = queue1.poll();TreeNode node2 = queue2.poll();if (node1.val != node2.val) {return false;}TreeNode left1 = node1.left, right1 = node1.right, left2 = node2.left, right2 = node2.right;if (left1 == null ^ left2 == null) {return false;}if (right1 == null ^ right2 == null) {return false;}if (left1 != null) {queue1.offer(left1);}if (right1 != null) {queue1.offer(right1);}if (left2 != null) {queue2.offer(left2);}if (right2 != null) {queue2.offer(right2);}}return queue1.isEmpty() && queue2.isEmpty();}
}

復雜度分析

時間復雜度：

O(min?(m,n))，其中 m 和 n 分別是兩個二叉樹的節點數。對兩個二叉樹同時進行廣度優先搜索，只有當兩個二叉樹中的對應節點都不為空時才會訪問到該節點，因此被訪問到的節點數不會超過較小的二叉樹的節點數。

空間復雜度：

O(min?(m,n))，其中 m?和 n 分別是兩個二叉樹的節點數。空間復雜度取決于隊列中的元素個數，隊列中的元素個數不會超過較小的二叉樹的節點數。

---

官方解法部分:

作者：力扣官方題解
鏈接：https://leetcode.cn/problems/same-tree/