文檔講解：代碼隨想錄

視頻講解：代碼隨想錄B站賬號

狀態：看了視頻題解和文章解析后做出來了

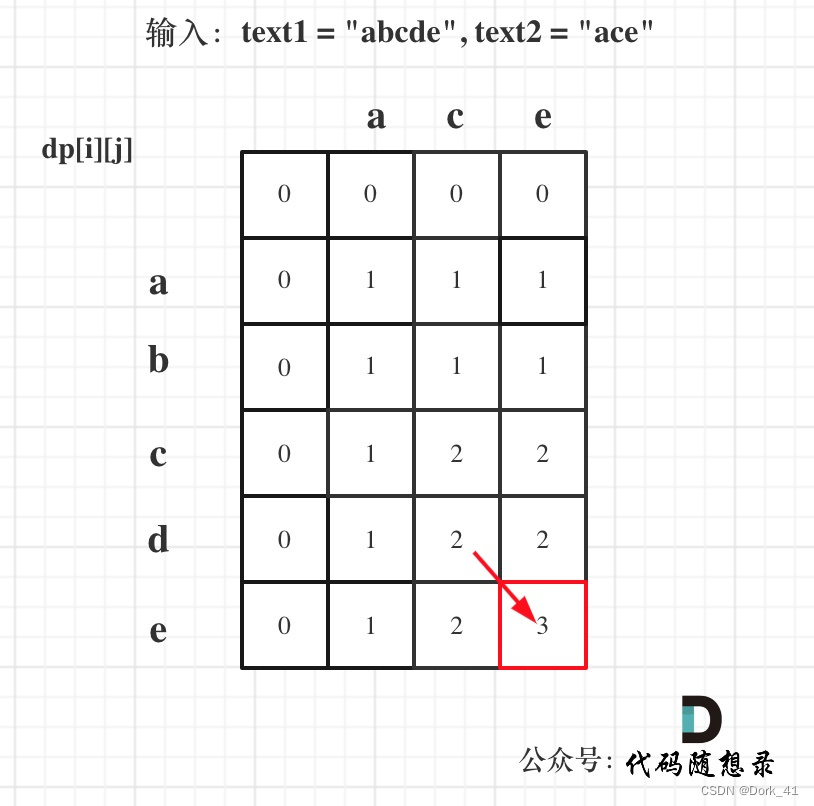
1143.最長公共子序列

class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]for i in range(1, len(text1) + 1):for j in range(1, len(text2) + 1):if text1[i-1] == text2[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])return dp[len(text1)][len(text2)]

• 時間復雜度：O(n^2)
• 空間復雜度：O(n)

1. 確定dp數組的含義

dp[i] 為下標范圍為0到i+1之間，最長的自增序列的長度。

2. 確定遞推公式

因為本題規定了自增序列可以不連續，所以我們不能只和前一個元素對比，而是和所有前面的元素對比，如果大于前面的某個元素，就在那個元素的基礎上+1，當然我們要一直保留最大值。

所以dp[i] = max(dp[j] + 1, dp[i])

其中i是當前元素，j是i之前的某個元素。

3. dp數組初始化

因為我們要返回的是長度，而每個元素單獨長度已經為1了，所以所有元素都先初始化為1。

4. 確定遍歷順序

遞推公式中的j是i之前的元素下標，所以從前往后遞推。

5. 舉例

1035.不相交的線

class Solution:def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:dp = [[0] * (len(nums2) + 1) for _ in range(len(nums1) + 1)]for i in range(1, len(nums1) + 1):for j in range(1, len(nums2) + 1):if nums1[i-1] == nums2[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])return dp[len(nums1)][len(nums2)]

• 時間復雜度：O(n^2)
• 空間復雜度：O(n)

和前一題完全一樣，改個變量名直接ac了。

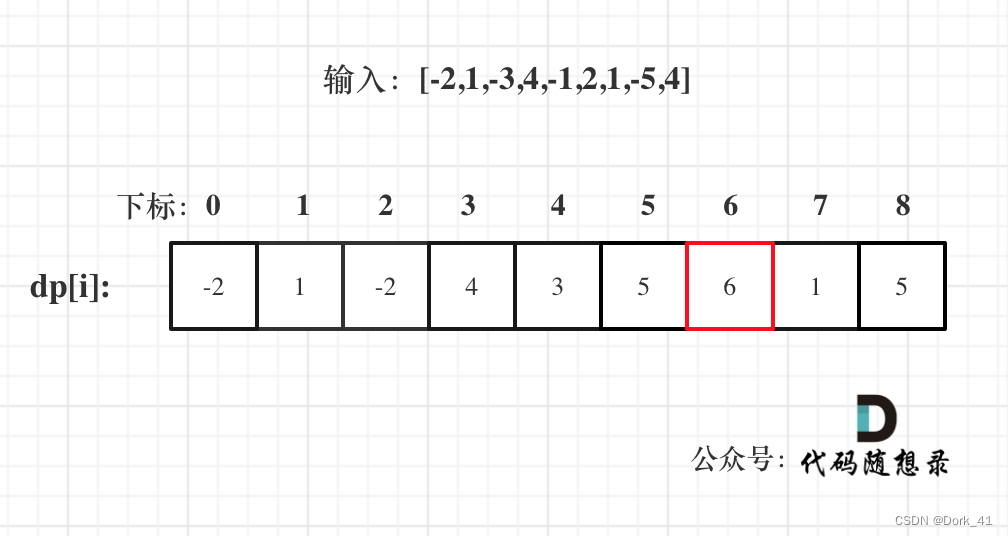
53. 最大子序和

class Solution(object):def maxSubArray(self, nums):dp = [0] * len(nums)dp[0] = nums[0]for i in range(1, len(nums)):dp[i] = max(dp[i-1] + nums[i], nums[i])return max(dp)

• 時間復雜度：O(n^2)
• 空間復雜度：O(n)

1. 確定dp數組的含義

dp[i] 為下標范圍為 0 到 i 之間的最大子序和。

2. 確定遞推公式

兩種情況：

第一種：取當前元素和上一個元素的最大子序和

第二種：不考慮之前元素，把當前元素當作起始點

通過比較這兩個值定義dp[i]的值。第二種的邏輯在于，如果當前元素的值都已經大于之前最大子序和 + 當前元素，那么之前子序和一定是負的，對于找到最大子序一定沒有幫助，那么還不如從當前元素開始另起一個子序。

3. dp數組初始化

dp[0]初始化為第一個元素的值，從第二個元素開始遍歷。

4. 確定遍歷順序

遞推公式需要之前的元素下標，所以從前往后遞推。

5. 舉例