文章目錄
- 鏈表結構(LinkedList)
- 鏈表以及數組的缺點
- 數組
- 鏈表的優勢
- 什么是鏈表?
- 封裝鏈表相關方法
- 源碼
- 鏈表常見面試題
- 237-刪除鏈表中的節點
- 206 - 反轉鏈表
- 數組和鏈表的復雜度對比
鏈表結構(LinkedList)
鏈表以及數組的缺點
- 鏈表和數組一樣,可以用于存儲一系列的元素,但是鏈表和數組的實現機制完全不同。
- 這一章中,我們就來學習一下另外一種非常常見的用于存儲數據的線性結構:鏈表。
數組
- 要存儲多個元素,數組(或稱為鏈表)可能是最常用的數據結構。
- 我們之前說過,幾乎每一種編程語言都有默認實現數組結構。
但是數組也有很多缺點
- 數組的創建通常需要申請一段連續的內存空間(一整塊的內存),并且大小是固定的(大多數編程語言數組都是固定的),所以當當前數組不能滿足容量需求時,需要擴容。(一般情況下是申請一個更大的數組,比如2倍。然后將原數組中的元素復制過去
- 而且在數組開頭或中間位置插入數據的成本很高,需要進行大量元素的位移。
- 盡管JavaScript的Array底層可以幫我們做這些事,但背后的原理依然是這樣。
鏈表的優勢
要存儲多個元素,另外一個選擇就是鏈表
但不同于數組,鏈表中的元素在內存中不必是連續的空間。
- 鏈表的每個元素有一個存儲元素本身的節點和一個指向下一個元素的引用(有些語言稱為指針或者鏈接)組成。
相對于數組,鏈表的優勢:
-
內存空間不是必須連續的。
√可以充分利用計算機的內存,實現靈活的內存動態管理。
-
鏈表不必再創建時就確定大小,并且大小可以無限的延伸下去。
-
鏈表在插入和刪除數據時,時間復雜度可以達到O(1)
√相對數組效率高很多
相對數組,鏈表的缺點:
- 鏈表訪問任何一個位置的元素時,都要從頭開始訪問。(無法跳過第一個元素訪問任何一個元素)。
- 無法通過下標直接訪問元素,需要從頭一個個訪問,直到找到對應元素。
什么是鏈表?
- 其實上面我們已經簡單的提過了鏈表的結構,我們這里更加詳細的分析一下。
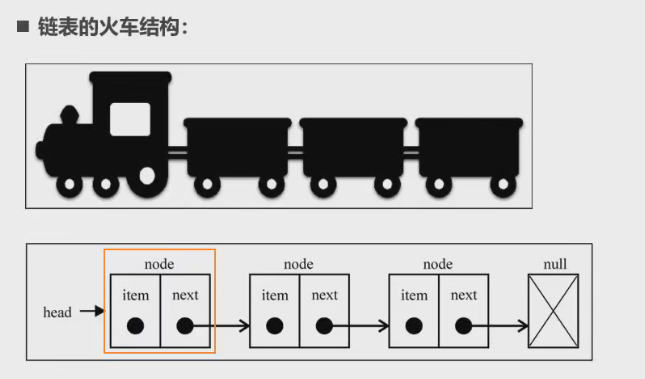
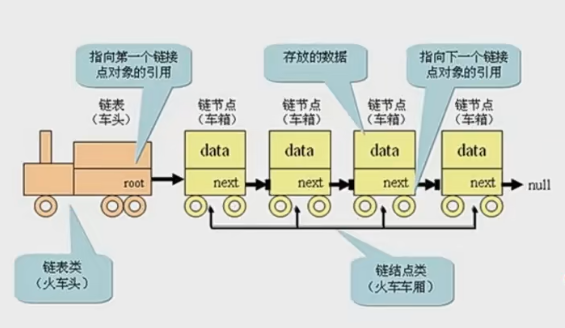
- 鏈表類似于火車:有一個火車頭,火車頭會連接一個節點,節點上有乘客(類似于數據),并且這個節點會連接下一個節點,以此類推。
封裝鏈表相關方法
我們先來認識一下,鏈表中應該有哪些常見的操作
append(element):向鏈表尾部添加一個新的項
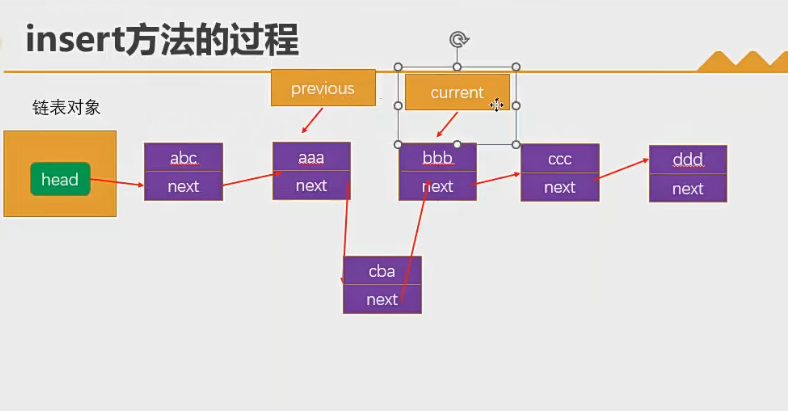
insert(position,element):向鏈表的特定位置插入一個新的項。
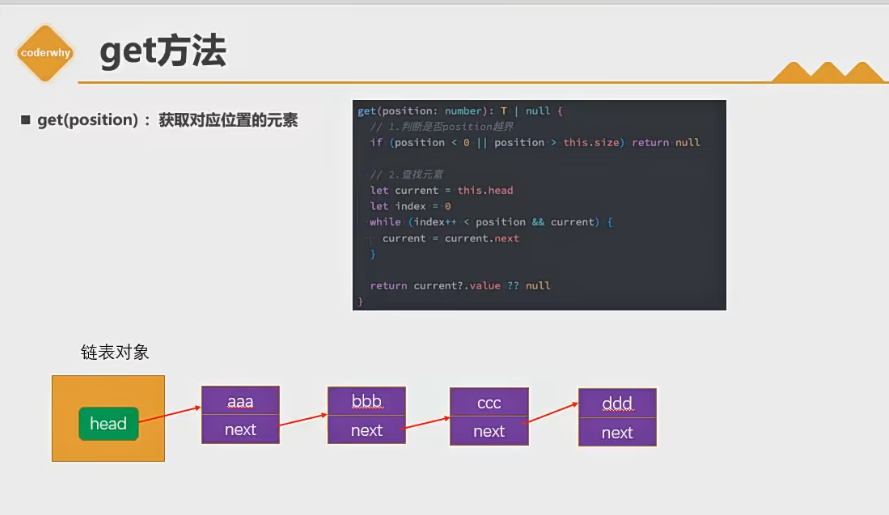
get(position):獲取對應位置的元素
indexOf(element):返回元素在鏈表中的索引。如果鏈表中沒有該元素則返回-1。
update(position,element):修改某個位置的元素
removeAt(position):從鏈表的特定位置移除一項。
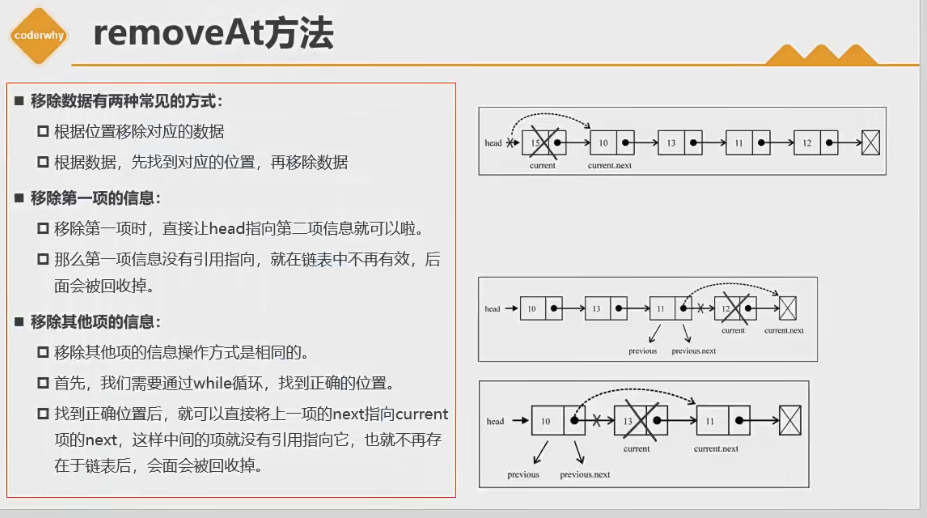
remove(element):從鏈表中移除一項。
isEmpty():如果鏈表中不包含任何元素,返回true,如果鏈表長度大于0則返回false。
size():返回鏈表包含的元素個數。與數組的length屬性類似。
源碼
// 1.創建Node節點類
class Node<T> {value: T;next: Node<T> | null = null;constructor(value: T) {this.value = value;}
}// 2.創建LinkedList的類
class LinkedList<T> {private head: Node<T> | null = null;private size: number = 0;get length() {return this.size;}// 封裝私有方法// 根絕positon獲取當前的節點(不是節點的value,而是獲取節點)private getNode(position: number): Node<T> | null {let index = 0;let current = this.head;while (index++ < position && current) {current = current.next;}return current;}// 追加節點append(value: T) {// 1.根據value新建一個Node節點const newNode = new Node(value);// 2.if (!this.head) {this.head = newNode;} else {let current = this.head;while (current.next) {current = current.next;}// current肯定指向最后一個節點current.next = newNode;}// 3.size++this.size++;}// 遍歷鏈表的方法traverse() {const values: T[] = [];let current = this.head;while (current) {values.push(current.value);current = current.next;}console.log(values.join(" -> "));}//鏈表插入元素的方法insert(value: T, position: number): boolean {// 1.越界判斷if (position < 0 || position > this.size) return false;// 2.根據value創建新的節點const newNode = new Node(value);/* 3.判斷* 是否插入頭部* 否則就找到需要插入的位置,然后記錄前一個節點和當前節點,在前一個節點的next等于newNode,newNode的next等于后一個節點*/if (position === 0) {newNode.next = this.head;this.head = newNode;} else {const previous = this.getNode(position - 1);newNode.next = previous!.next;previous!.next = newNode;}this.size++;return true;}//鏈表插入元素的方法removeAt(position: number): T | null {// 1.越界判斷if (position < 0 || position >= this.size) return null;let current = this.head;if (position === 0) {this.head = current?.next ?? null;} else {const previous = this.getNode(position - 1);previous!.next = previous?.next?.next ?? null;}this.size--;return current?.value ?? null;}// 獲取方法get(position: number): T | null {if (position < 0 || position >= this.size) return null;return this.getNode(position)?.value ?? null;}// 更新方法update(value: T, position: number): boolean {if (position < 0 || position >= this.size) return false;const currentNode = this.getNode(position);currentNode!.value = value;return true;}// 根據值獲取該值位置索引indexOf(value: T): number {let current = this.head;let index = 0;while (current) {if (current.value === value) {return index;}index++;current = current.next;}return -1;}// 刪除方法,根據value刪除remove(value: T): T | null {const index = this.indexOf(value);return this.removeAt(index);}// 判斷單鏈表是否為空的方法isEmpty() {return this.size === 0;}
}export {};鏈表常見面試題
237-刪除鏈表中的節點
- https://leetcode.cn/problems/delete-node-in-a-linked-list/
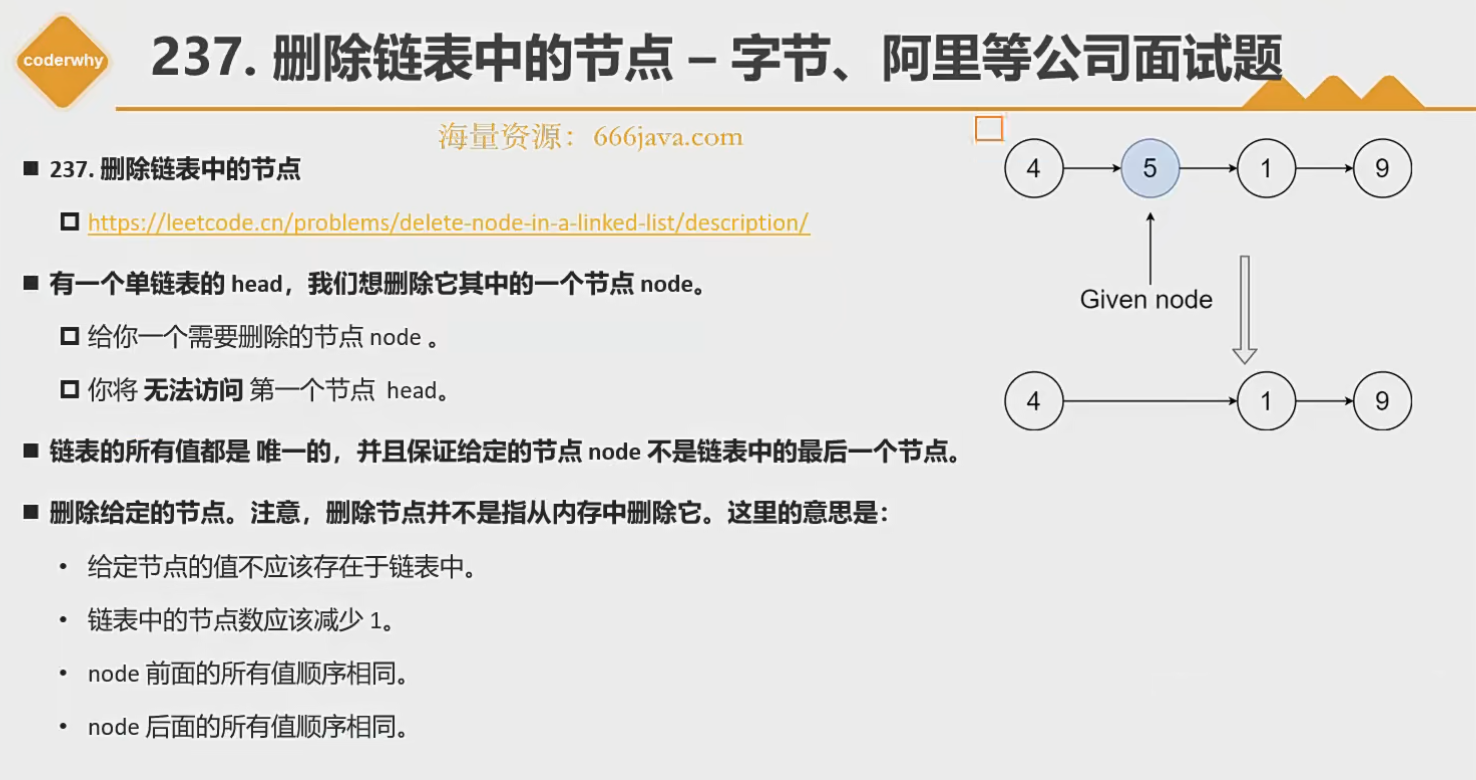
解題
// Definition for singly-linked list.
class ListNode {val: number;next: ListNode | null;constructor(val?: number, next?: ListNode | null) {this.val = val === undefined ? 0 : val;this.next = next === undefined ? null : next;}
}/**Do not return anything, modify it in-place instead.*/
function deleteNode(node: ListNode | null): void {node!.val = node!.next!.valnode!.next = node!.next!.next
}206 - 反轉鏈表
- https://leetcode.cn/problems/reverse-linked-list/

- 用棧結構解決
function reverseList(head: ListNode | null): ListNode | null {if(head === null) return nullif(head.next === null) return headconst stack:ListNode[] = []let current:ListNode | null = headwhile(current) {stack.push(current)current = current.next}const newHead:ListNode = stack.pop()!let newHeadCurrent = newHeadwhile(stack.length) {const node = stack.pop()!newHeadCurrent.next = nodenewHeadCurrent = newHeadCurrent.next}newHeadCurrent.next = nullreturn newHead
};
- 用非遞歸解題
function reverseList(head: ListNode | null): ListNode | null {if (head === null || head.next === null) return head;let newHead: ListNode | null = null;// 1.next = 2, 2.next = 3, 3.next = 4while (head) {// 讓current指向下一個節點// 目的:保留下個節點的引用,可以拿到,并且不會銷毀(current = 2)const current= head.next;// 改變head當前指向的節點,指向newHead// 這里反轉鏈表對于第一節點來說,指向newHead就是null(1.next = null)head.next = newHead;// 讓newhead指向head節點// 這里開始準備反轉新的節點,目的是下一次遍歷時,可以讓下一個節點指向第一個節點(newHead = 1)newHead = head;// 讓head指向下個節點也就是current(head = 2)head = current;}return newHead;
}

- 用遞歸方案解題
function reverseList(head: ListNode | null): ListNode | null {// 遞歸停止條件,當遞歸到最后一個節點時停止if (head === null || head.next === null) return head;// 一直遞歸循環直到符合head === null 時停止遞歸// 那么拿到的就是鏈表倒數第二個節點const newHead = reverseList(head.next ?? null)// 反轉鏈表,讓最后一個節點指向head開始正式反轉head.next.next = head// 讓倒數第二個節點的next指向nullhead.next = null// 最后遞歸完了就是反轉后的鏈表了return newHead
}
數組和鏈表的復雜度對比
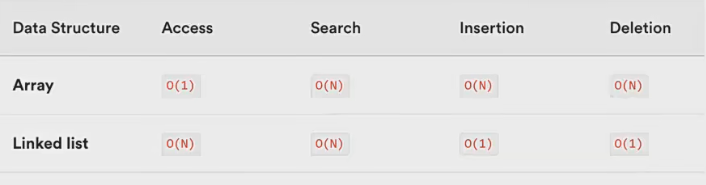
接下來,我們使用大O表示法來對比一下數組和鏈表的時間復雜度:
-
數組是一種連續的存儲結構,通過下標可以直接訪問數組中的任意元素。
-
時間復雜度:對于數組,隨機訪問時間復雜度為o(1),插入和刪除操作時間復雜度為o(n)。
-
空間復雜度:數組需要連續的存儲空間,空間復雜度為o(n)。
-
鏈表是一種鏈式存儲結構,通過指針鏈接起來的節點組成,訪問鏈表中元素需要從頭結點開始遍歷。
-
時間復雜度:對于鏈表,隨機訪問時間復雜度為o(n),插入和刪除操作時間復雜度為o(1)。
-
空間復雜度:鏈表需要為每個節點分配存儲空間,空間復雜度為O(n)。
-
在實際開發中,選擇使用數組還是鏈表需要根據具體應用場景來決定。
-
如果數據量不大,且需要頻繁隨機訪問元素,使用數組可能會更好。
-
如果數據量大,或者需要頻繁插入和刪除元素,使用鏈表可能會更好。












)


)



