2022年MathorCup高校數學建模挑戰賽—大數據競賽
A題 58到家家政服務訂單分配問題
原題再現:
??“58 到家”是“58 同城”旗下高品質、高效率的上門家政服務平臺,平臺向用戶提供家政保潔、保姆、月嫂、搬家、維修等眾多生活領域的服務。在家政保潔場景中,用戶在平臺下單購買服務后,平臺會將訂單分配給一個保潔阿姨,阿姨接到訂單后按照用戶指定的服務時間上門,進行保潔服務。平臺在將訂單分配給一個保潔阿姨時,一方面,為了提高對顧客的服務質量,需要盡量分配服務分較高的阿姨,其中阿姨的服務分是基于阿姨歷史訂單的評價情況得到,取值為[0,1],值越大越好;另一方面,為了幫助阿姨提高接單量,需要盡量縮短阿姨相鄰單之間的通行時間。
??每天通過平臺進行分配的訂單量是巨大的,當前平臺實現了一套訂單分配算法,本問題研究的是如何優化系統的分配算法,提高算法的求解能力,實現提升顧客體驗、節省阿姨時間。
??數據說明:
??數據包含一天內、一個區域的所有訂單和所有保潔阿姨。


??約束條件及假設:
??1. 所有訂單都要分配一個且只有一個阿姨;
??2. 每個訂單需要指定一個服務開始時間,這個時間的取值范圍為 [最早時間,最晚時間],且是半點的整數倍;
??3. 一個阿姨同時只能服務一個訂單;
??4. 阿姨需要在每個訂單的服務開始時間之前到達客戶位置;
??5. 阿姨每天開始任務時必須從初始點位置出發;
??6. 任意兩點的距離為歐式距離;
??7. 保潔阿姨的行駛速度為 15 千米/小時。 優化目標:
??將每個訂單匹配阿姨時,優化的目標是:
??1. 所有訂單匹配的阿姨的服務分,其平均值 A 盡可能大;
??2. 最小化每單的平均通行距離 B。一個訂單的通行距離指的是阿姨從上一個地點到本單地點的距離(歐式距離),其中阿姨第一個訂單的通行距離等于從初始點到第一個訂單位置的距離,單位是千米;
??3. 最小化阿姨服務訂單的平均間隔時間 C。一個訂單的間隔時間指的是,阿姨從上一個單服務結束時刻到本單服務開始時刻的時間間隔,單位是小時,其中阿姨第一個訂單的間隔時間設定為 0.5 小時(阿姨首單需要做基本的準備工作,不考慮阿姨從初始點到第一個訂單的通行時間);
??4. 總體目標是各個目標的加權和:αA-βB-γC,其中α=0.78、β=0.025、γ=0.195,得分四舍五入取 6 位小數。目標值越大越好。
??初賽問題
??問題 1:只考慮離線批量派單模式。附件 1 與附件 2 中分別給出的是一天的所有訂單信息與阿姨信息。
??(a) 請設計最優的訂單與阿姨匹配算法,將所有訂單進行分配,并將求解結果填寫到 result1.txt 中。(訂單必須全部分配、阿姨不需要全部匹配訂單)。
??(b) 基于(a)的算法,請對附件 1 中的前 50 個訂單與附件 2 中前 20 個阿姨,重新運行算法,給出阿姨的執行任務列表,并畫出阿姨的行動軌跡圖。

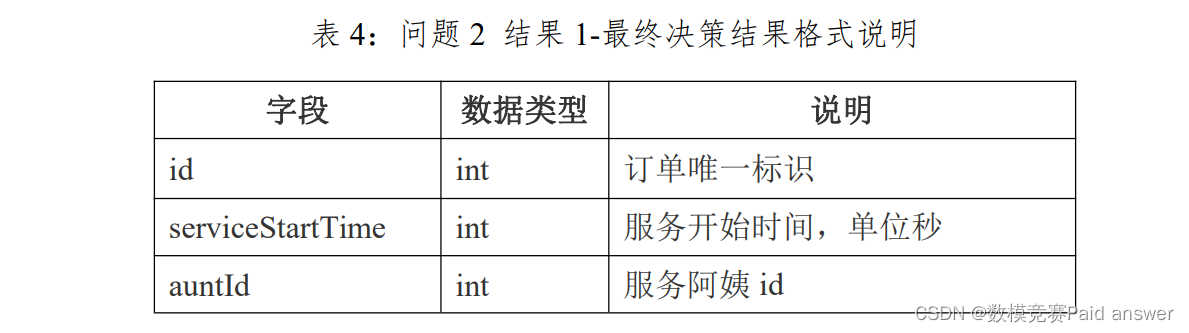
??問題 2:線上批量派單模式。在實際業務場景中,通常采用固定的頻率派單,每 30 分鐘將該段時間內產生的新訂單統一分配;分配時允許部分訂單暫時不派單,稱之為壓單,但是壓單訂單必須滿足服務開始時間的最早時 間 比 當 前 時 間 晚 于 2 個 小 時 ( 不 包 括 2 個 小 時 ) 也 即 滿足:serviceFirstTime-currentTime>2h;請設計這種情況下的每批訂單的最優分配算法。并將求解結果 1-最終決策結果填寫到 result21.txt 中,結果 2-每次決策結果填寫到 result22.txt 中。

整體求解過程概述(摘要)
??隨著我國經濟水平的發展和人民生活質量的提高,人們對家政服務的要求日益專業化、規范化、綜合化,為增強客戶體驗及提高時間效率,探究家政服務公司訂單分派系統的優化問題,我們通過貪心算法的思想,設計基于收益評估的阿姨與訂單分配算法,來研究如何在離線批量派單時達到收益最大,接著引入下單時間對模型進行改進,建立多批次的分配模型,實現訂單的多批次分配。
??針對問題一,首先根據題意定義決策變量,并將題中所給的約束條件、優化目標等轉化為具體的數學規劃模型。然后因為是離線派單模式,因此所有訂單的信息都是已知的,考慮到問題的規模較大,我們根據數學規劃模型設計基于收益評估的阿姨與訂單分配算法。該算法首先通過貪心算法定義每個訂單的服務優先級,然后將訂單按照客戶要求的最晚服務時間進行升序排序,若是最晚服務時間相同則按照優先級進行降序;再給每一個訂單進行每個阿姨的預分配,依據貪心算法預測出每個符合條件的阿姨在分配給該訂單的情況下的收益,然后根據具體的收益情況進行阿姨分配。最終通過上述算法建立基于收益評估的阿姨與訂單分配模型,決策出各個訂單的分派方案,并繪制所有訂單分配最大收益的頻數直方圖和阿姨分派次數的統計圖對結果進行可視化,發現最大收益集中分布在區間 [0.55,0.65] 上,且阿姨的重復分配率高,絕大部分阿姨未被分配,高達2110個,最終計算出該算法下的最優總體目標為0.611404。接著我們針對前50個訂單與前20個阿姨進行分派,并計算出該數據集下的總體目標為0.477170,并繪制出分派過的阿姨的行動軌跡圖。
??針對問題二,根據題意需要考慮下單時間這一因素,根據固定的頻率將訂單根據下單時間進行分批,每次只能在已知當前批次訂單和被壓單訂單的情況下進行最優的阿姨分派。因此我們對問題一的模型進行改進,設計基于收益評估的多批次阿姨與訂單分配模型。主要原理是組建當前批次訂單并對當前批次訂單進行阿姨預分配的收益預測,然后選出當前收益最大的分配情況和壓單情況,再對下一批訂單進行分配。因為在優先級機制的保障下,最先分配阿姨的訂單一定是時間上較為緊急的訂單,因此在處理后面幾個訂單時,如果符合壓單且預分配收益小于事先定義的閾值,則對其進行壓單。我們對閾值進行參數尋優,從而確定最優閾值為 0.67,接著通過上述模型決策出問題二各批次訂單的分配結果和每次決策結果,并繪制所有訂單分配最大收益的頻數直方圖和阿姨分派次數的統計圖對結果進行可視化,發現問題二的直方圖集中數據區間與問題一相似,但未被分派的阿姨數量減少,最終計算出該方案下的最優總體目標為 0.612838,總壓單次數為 5494 次。
??最后我們編寫 C++代碼對模型進行檢驗,發現問題一和問題二的訂單分派結果均通過檢驗,說明不存在一個阿姨同時服務多個訂單或訂單漏分配的情況,訂單分派合理。
模型假設:
??1) 假設顧客不會隨意取消訂單。
??依據:當前訂單的取消可能會導致需要對后續訂單進行重新分配才能保證最優目標。
??2) 假設阿姨體力充足,無訂單服務次數限制。
??依據:阿姨存在一天服務多個訂單的情況。
??3) 假設阿姨每次通行和服務時無突發情況。
??依據:意外的發生會影響該阿姨后續訂單的分派。
問題分析:
??數據的預處理分析
??首先通過程序檢測各個文件,發現各文件都不存在缺失值。然后通過編寫 C++ 代碼,將訂單信息的時間戳轉換為具體日期,發現所有訂單中的服務時間都在一天內,為2022 年 9 月 10 日當天的 8:00 至 22:00,因此只需針對當天進行訂單分派工作。
??問題一的分析
??針對問題一,首先根據題意定義決策變量,并將題中所給的約束條件、優化目標等轉化為具體的數學規劃模型。然后因為是離線派單模式,因此所有訂單的信息都是已知的,考慮到問題的規模較大,我們設計基于收益評估的阿姨與訂單分配算法:首先通過貪心算法3定義每個訂單的服務優先級,將訂單按照客戶要求的最晚服務時間進行升序排序,若是最晚服務時間相同則按照優先級進行降序;再給每一個訂單進行阿姨的預分配,預測出每個符合條件的阿姨分配給該訂單的收益,然后根據收益情況進行具體的阿姨分配。最終通過上述算法建立基于收益評估的阿姨與訂單分配模型,并給出問題一的計算結果和繪制前 50 個訂單與前 20 個阿姨的行動軌跡圖。
??問題二的分析
??針對問題二,根據題意我們需要引入下單時間這一因素,根據固定的頻率將訂單根據下單時間進行分批,每次只能在已知當前批次訂單的情況下進行最優的阿姨分派。因此我們對問題一的模型進行進一步加工,將其設計成基于收益評估的多批次阿姨與訂單分配模型,實現訂單的在線調度4。次進行訂單收益對當前批次訂單進行阿姨預分配的收益預測,然后選出當前最高收益5的分配情況,再對下一批訂單進行分配。針對符合壓單情況的訂單,因為我們在優先級的保障下,最先分配阿姨的訂單一定是時間上較為緊急的訂單,因此在處理后面幾個訂單的適合,如果符合壓單且預分配收益小于閾值,則對其進行壓單。最終我們通過上述模型計算出問題二的最終決策結果和每次決策結果。
模型的建立與求解整體論文縮略圖


全部論文及程序請見下方“ 只會建模 QQ名片” 點擊QQ名片即可
程序代碼:
程序如下:
#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
#include <stack>
#include <queue>
using namespace std;void backTrack(vector<vector<double>>& num,vector<bool>&used, vector<int>& pre,vector<int>& cur,double curProfit, double&preProfit, int n, int pos)
{//如果pos == n 說明行數已經達到n行,所有的行都已經選完,是一種結果if (pos == n) {//全局找最大,判斷是否出現更優解if (curProfit > preProfit) {//更新當前最大的和preProfit = curProfit;//數組賦值,將這個最優解的數組賦值給pre,最后用來輸出pre = cur; }return;}//枚舉第pos行的每一列for (int i = 0; i < n; i++){//改行必須在之前沒有被選擇使用過,必須滿足題意if (!used[i]) // 標記第 i列,下一次第i列就不能選擇了{//代表本次選擇pos行的i列元素,進行標記本次遞歸的選擇位置//因為可能出現本次選擇是最優的情況,所以需要保存cur[pos] = i; // 記錄每一個 pos行對應的列數i,下面的就是回溯過程//代表當前的評分和加上本次的選擇//同理和cur一樣都要保存curProfit += num[pos][i];//代表著第i例被使用過,下次不能在選擇第i列used[i] = true;backTrack(num,used,pre,cur, curProfit, preProfit, n, pos + 1);//撤銷選擇curProfit -= num[pos][i];//撤銷標記used[i] = false;}}
}int main()
{int n;while (cin >> n){vector<vector<double>> vvd(n, vector<double>(n));for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){cin >> vvd[i][j];}}vector<int> pre(n); // 記錄最優解的每個值 所在的 列數vector<int> cur(n); // 列數加入數組vector<bool> used(n); // 標記數組, 因為一列只能選擇一個double preProfit = INT_MIN; // 全局的最大值double curProfit = 0.0; // 當前的最大值int pos = 0; // pos就是行數,pos到達一行,就選y值就可以了backTrack(vvd, used, pre, cur, curProfit, preProfit, n, pos); //打印結果printf("%4.2f\n",preProfit);//cout << preProfit << endl;for (int i = 0; i < pre.size(); i++){cout << i + 1 << " " << pre[i] + 1 << endl;}}
}


)



聊天API使用指導)












