好久不見~我又回來了

這一節我們來講一講圖像在計算機中的本質，以及全連接神經網絡的缺陷，進而引出卷積神經網絡

---

一、圖像在計算機中的本質

不知道你有沒有學過數據結構，在講這一部分的時候對數組進行了擴展，講到了廣義表和壓縮矩陣，其中壓縮矩陣用來壓縮圖像信息進行傳遞。

在計算機中，圖像本質上是一個數字矩陣。每個像素點對應一個數值，表示顏色或亮度信息。
具體來說：

• 對于灰度圖像，它是一個二維矩陣 $I\in {\mathbb{R}}^{H\times W}$，其中 $H$ 是高度（行數），$W$ 是寬度（列數），每個元素 $I(i,j)$ 表示像素在位置 $(i,j)$ 的灰度值（范圍通常為 $0$ 到 $255$）。

• 例如下面這兩張圖

• 

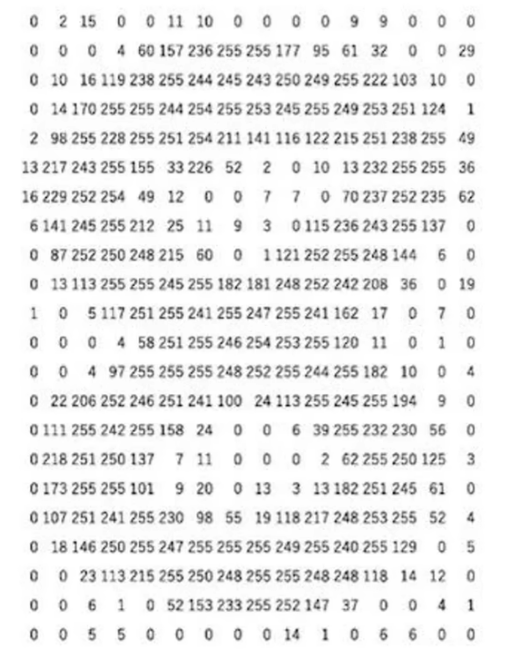
• 對于彩色圖像（如 RGB 格式），它是一個三維張量 $I\in {\mathbb{R}}^{H\times W\times C}$，其中 $C$ 是通道數（通常 $C=3$，對應紅、綠、藍三個通道）。每個元素 $I(i,j,k)$ 表示位置 $(i,j)$ 在通道 $k$ 的顏色強度。

例如，一個 $32\times 32$ 的 RGB 圖像可表示為：
$$I=\left[\begin{array}{ccc}[I_{11}^R,I_{11}^G,I_{11}^B]& ?& [I_{1W}^R,I_{1W}^G,I_{1W}^B]\\ ?& ?& ?\\ [I_{H1}^R,I_{H1}^G,I_{H1}^B]& ?& [I_{HW}^R,I_{HW}^G,I_{HW}^B]\end{array}\right]$$
這種表示方式便于計算機處理，但圖像數據通常維度很高（尤其是彩色圖片，如 $1000\times 1000$ 像素的圖像有 $10^6$ 個元素），這給數據存儲和神經網絡處理帶來了挑戰。

二、壓縮矩陣

針對復雜的彩色圖片，圖像壓縮是必要的
原始圖像矩陣通常包含大量冗余數據（如相鄰像素相似），導致文件大小過大，不利于存儲或傳輸。壓縮的目標是減少數據量，同時保持視覺質量。
壓縮分為兩類：

• 無損壓縮：保留所有原始數據，如PNG格式，使用矩陣操作（如游程編碼）。
• 有損壓縮：犧牲少量細節以換取更高壓縮率，如JPEG格式，基于矩陣變換（如離散余弦變換）

壓縮過程直接操作圖像矩陣：
變換編碼：將圖像矩陣轉換為頻域表示，減少空間冗余。例如，在JPEG壓縮中，圖像被分成8×8塊，每個塊通過離散余弦變換（DCT）轉換為系數矩陣。DCT公式為： $$F(u,v)=\frac{2}{N}C(u)C(v)\sum _{i=0}^{N?1}\sum _{j=0}^{N?1}f(i,j)\cos \left(\frac{(2i+1)u\pi }{2N}\right)\cos \left(\frac{(2j+1)v\pi }{2N}\right)$$ 其中$N=8$，$f(i,j)$是原始像素矩陣元素，$F(u,v)$是變換后的系數矩陣元素。
量化：壓縮矩陣通過量化表（另一個矩陣）縮放DCT系數，丟棄高頻細節（人眼不敏感部分），實現數據壓縮。量化公式為： $$Q(u,v)=\text{round}\left(\frac{F(u,v)}{Q_{\text{table}}(u,v)}\right)$$ 其中$Q_{\text{table}}$是預定義的量化矩陣。
編碼：量化后的矩陣通過熵編碼（如Huffman編碼）進一步壓縮為二進制流。
關系總結：圖像矩陣是壓縮的起點，壓縮算法生成新的“壓縮矩陣”（如DCT系數矩陣），最終輸出為壓縮文件。解壓時，逆過程重建近似原矩陣。
當然這一部分要求線代基礎知識，看不懂沒有關系，了解即可

三、全連接神經網絡的缺陷

全連接神經網絡（FCNN）在處理圖像時存在嚴重缺陷，主要源于其結構：

• 參數爆炸問題：在 FCNN 中，每個輸入節點（像素）都連接到隱藏層所有節點。設輸入大小為 $n$（如圖像展平為向量 $x\in {\mathbb{R}}^n$），隱藏層大小為 $m$，則權重矩陣 $W\in {\mathbb{R}}^{m\times n}$ 的參數數量為 $m\times n$。對于 $H\times W$ 的圖像，$n=H\times W$（灰度）或 $n=H\times W\times C$（彩色）。例如，$1000\times 1000$ 的 RGB 圖像輸入，$n\approx 3\times 10^6$，若隱藏層 $m=1000$，參數量高達 $3\times 10^9$，導致訓練困難、內存不足。
• 計算效率低下：前向傳播的計算復雜度為 $O(m\times n)$，在圖像任務中計算量巨大，難以實時處理。
• 缺乏局部性：FCNN 忽略圖像的空間結構。每個像素獨立處理，無法有效捕捉局部特征（如邊緣、紋理），因為相鄰像素在計算中不共享權重。
• 過擬合風險高：高參數量使模型容易過擬合小數據集，泛化能力差。
• 無平移不變性：圖像中物體位置變化（如貓在左或右）會導致輸出劇烈變化，因為權重與絕對位置綁定。

這些缺陷使 FCNN 不適合圖像任務，需要更高效的架構。

四、卷積神經網絡

為解決 FCNN 的缺陷，卷積神經網絡（CNN）被引入。它利用圖像的空間局部性和平移不變性：

• 卷積層：使用卷積核（filter）在圖像上滑動，計算局部區域的內積。設輸入圖像 $X\in {\mathbb{R}}^{H\times W\times C}$，卷積核 $K\in {\mathbb{R}}^{F_h\times F_w\times C\times D}$（$F_h,F_w$ 為核大小，$D$ 為輸出通道數），輸出特征圖 $Y$ 的元素為：
  $$Y(i,j,d)=\sum _{m=0}^{F_h?1}\sum _{n=0}^{F_w?1}\sum _{c=0}^{C?1}K(m,n,c,d)?X(i+m,j+n,c)$$
  這實現了權重共享和稀疏連接，大幅減少參數（如 $3\times 3$ 核僅需 $9\times C\times D$ 參數）。
• 優勢：
  • 參數高效：卷積核在整張圖像共享權重，避免參數爆炸。
  • 局部特征提取：捕捉邊緣、角點等局部模式。
  • 平移不變性：物體位置變化不影響特征檢測。
  • 層次結構：通過多層卷積和池化，逐步抽象特征（從低級紋理到高級語義）。

CNN 的典型結構包括卷積層、激活函數（如 ReLU）、池化層和全連接層。以下是一個簡單 CNN 的 PyTorch 實現示例：

import torch
import torch.nn as nnclass SimpleCNN(nn.Module):def __init__(self, num_classes=10):super(SimpleCNN, self).__init__()# 卷積層: 輸入通道3 (RGB), 輸出通道16, 核大小3x3self.conv1 = nn.Conv2d(3, 16, kernel_size=3, stride=1, padding=1)# 池化層: 2x2 最大池化self.pool = nn.MaxPool2d(kernel_size=2, stride=2)# 全連接層: 輸入尺寸基于圖像大小 (假設輸入32x32)self.fc = nn.Linear(16 * 16 * 16, num_classes)  # 池化后尺寸減半: 32/2=16def forward(self, x):x = self.pool(torch.relu(self.conv1(x)))  # 卷積 + ReLU + 池化x = x.view(x.size(0), -1)  # 展平x = self.fc(x)return x# 示例用法
model = SimpleCNN()
input_image = torch.randn(1, 3, 32, 32)  # 批大小1, 通道3, 高度32, 寬度32
output = model(input_image)
print(output.shape)  # 輸出: torch.Size([1, 10])

此代碼展示了 CNN 如何高效處理圖像：卷積層提取特征，池化層降維，全連接層分類。CNN 已成為計算機視覺的基石，廣泛應用于圖像識別、目標檢測等任務。

---

總結一下：圖像在計算機中是矩陣方式進行存儲的，而CNN卷積神經網絡能夠高效處理圖像，下一節我們來詳細分析CNN的整體架構