DFS序和歐拉序的降維打擊

1. DFS 序和時間戳

1.1 DFS 序

定義：樹的每一個節點在深度優先遍歷中進、出棧的時間序列。

如下樹的 dfs 序就是[1,2,8,8,5,5,2,4,3,9,9,3,6,6,4,7,7,1]。

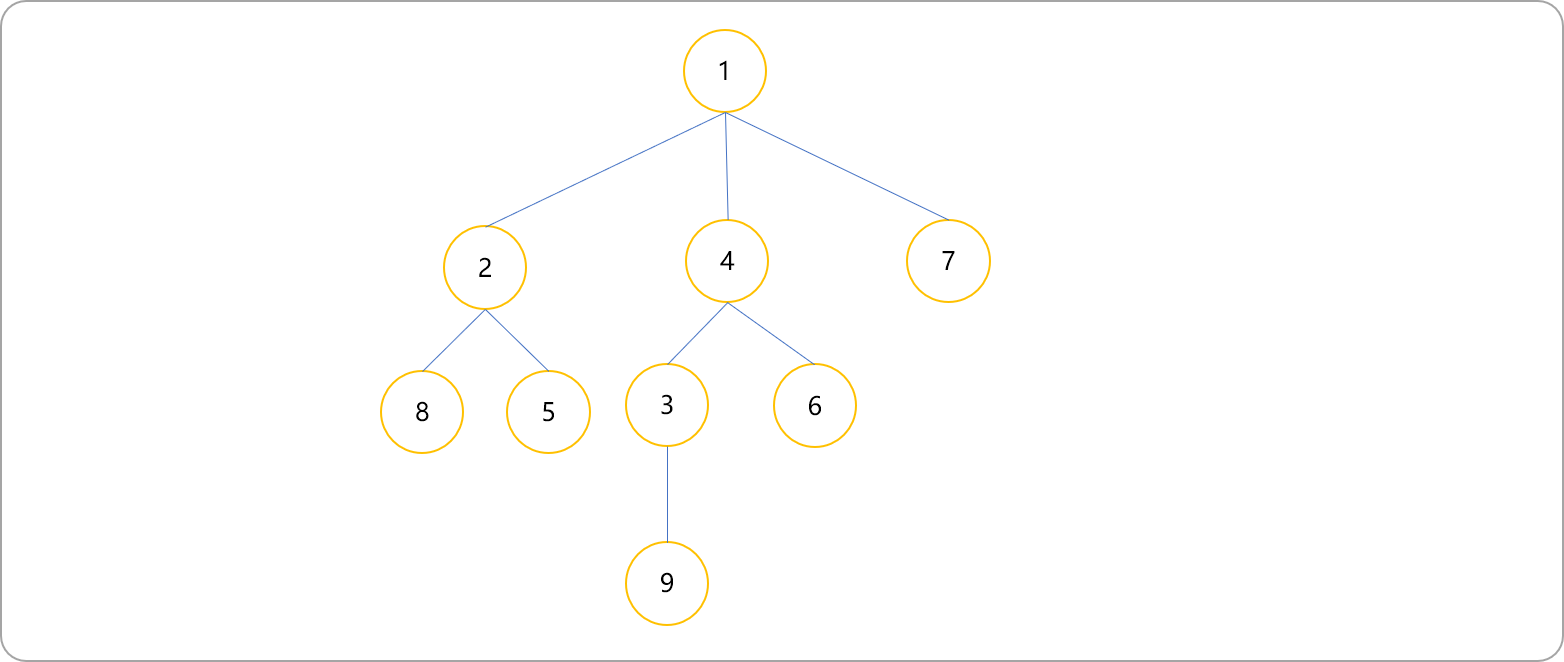
下圖為生成DFS的過程。對于一棵樹進行DFS序，除了進入當前節點時對此節點進行記錄，同時在回溯到當前節點時對其也記錄一下，所以DFS序中一個節點的信息會出現兩次。

Tips： 因為在樹上深度搜索時可以選擇從任一節點開始，所以DFS序不是唯一的。

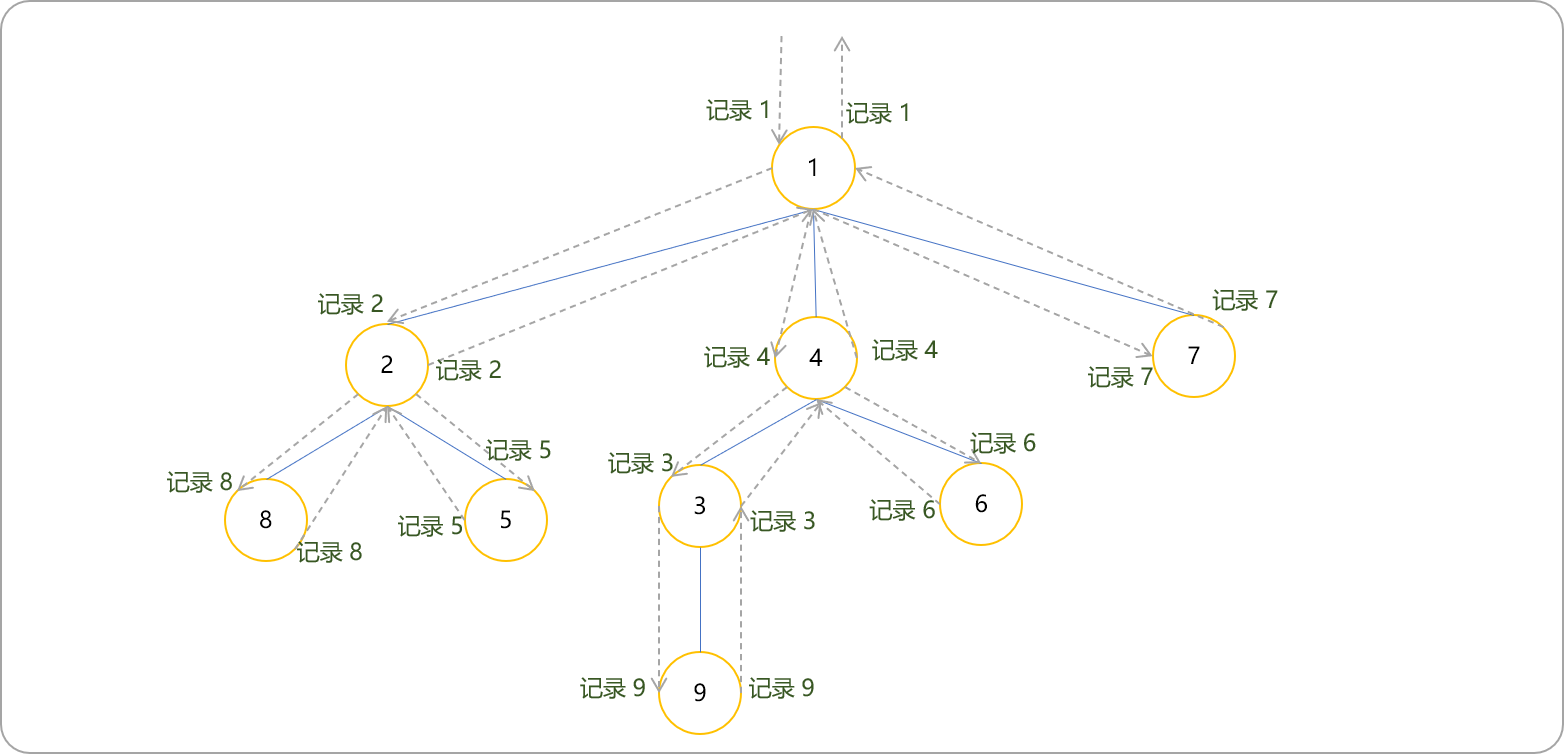
DFS序的特點：

可以把樹數據結構轉換為線性數據結構，從而可以把基于線性數據的算法間接用于處理樹上的問題。堪稱降維打擊。
相同編號之間的節點編號為以此編號為根節點的子樹上的所有節點編號。

[2,8,8,5,5,2]表示編號 2為根節點的子樹中所有節點為8,5。

[4,3,9,9,3,6,6,4]表示編號 4為根節點的子樹中所有節點為 3,9,6。
如果一個節點的編號連續相同，則此節點為葉節點。
樹的DFS序的長度是2N（N表示節點的數量）。

求DFS序的代碼：

#include <cstdio>
using namespace std;
const int maxn=1e5+10;
int n;
int tot,to[maxn<<1],nxt[maxn<<1],head[maxn];
int id[maxn],cnt;
void add(int x,int y)
{to[++tot]=y;nxt[tot]=head[x];head[x]=tot;
}
void dfs(int x,int f)
{id[++cnt]=x;for(int i=head[x];i;i=nxt[i]){int y=to[i];if(y==f)continue;dfs(y,x);}id[++cnt]=x;
}
int main()
{scanf("%d",&n);for(int i=1;i<n;i++){int x,y;scanf("%d%d",&x,&y);add(x,y);add(y,x);}dfs(1,0);for(int i=1;i<=cnt;i++)printf("%d ",id[i]);return 0;
}

測試數據：

1.2 時間戳

按照深度優先遍歷的過程，按每個節點第一次被訪問的順序，依次給予這些節點1?N的標記，這個標記就是時間戳。如果一個點的起始時間和終結時間被另一個點包括，這個點肯定是另一個點的子節點（簡稱括號化定理）。每棵子樹 x 在 DFS 序列中一定是連續的一段，結點 x 一定在這段的開頭。

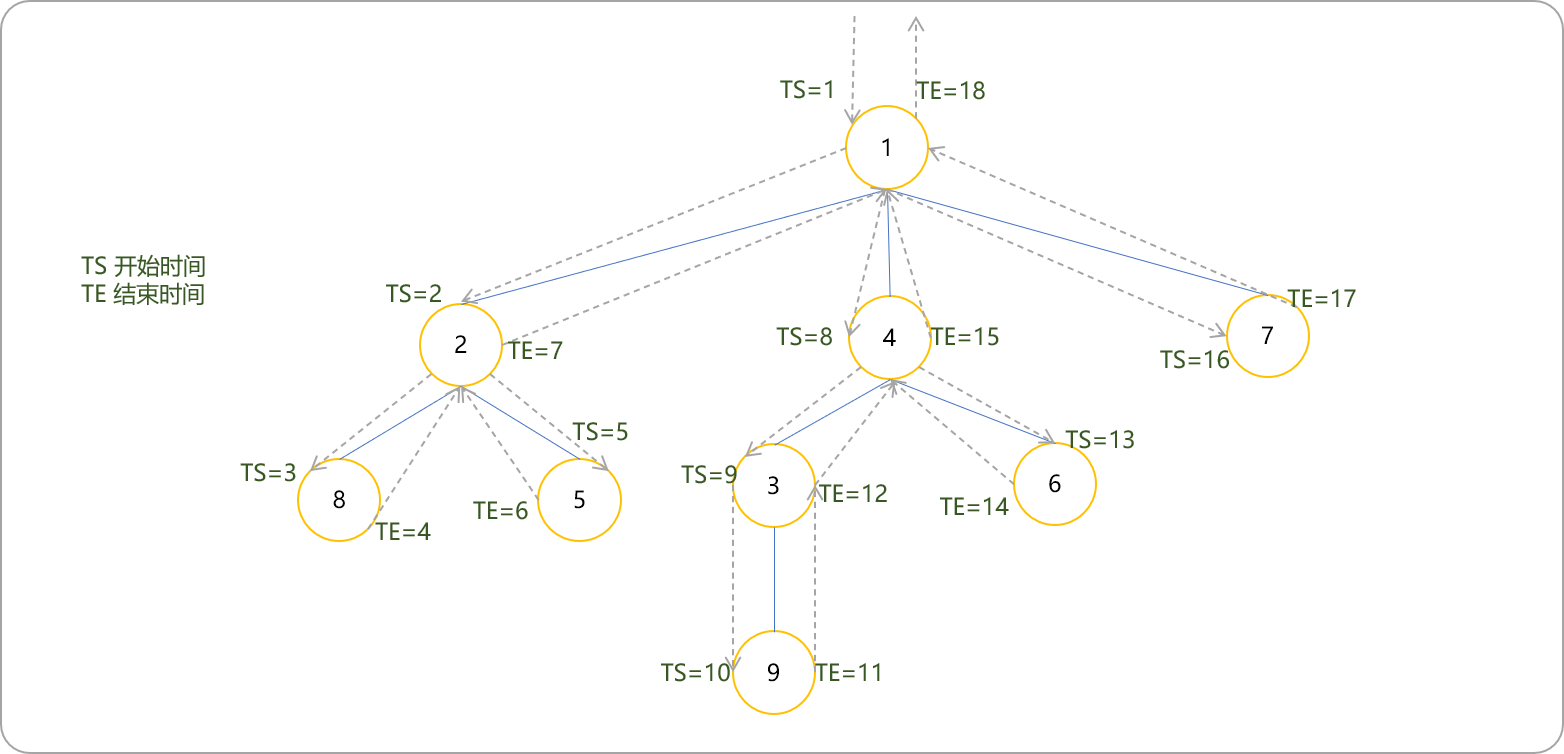
dfs與時間戳的關系，對應列表中索引號和值的關系。

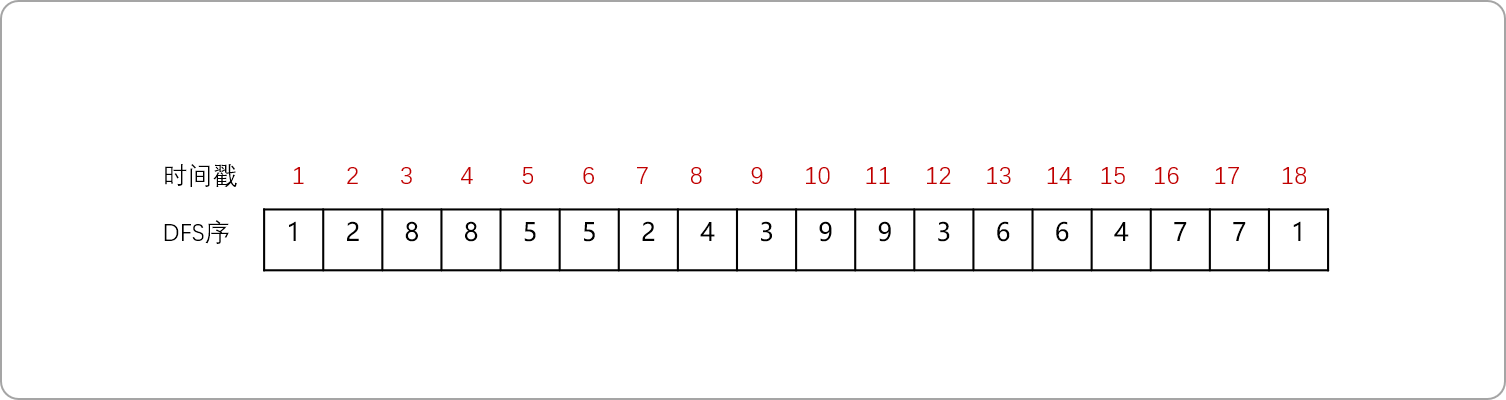
在dfs代碼中添加進入節點時的順序和離開節點時的順序。

//……
//in 開始時間 out 結束時間
int in[maxn],out[maxn];
//……
void dfs(int x,int f) {//節點的 dfs 序id[++cnt]=x;//開始時間in[x]=cnt;for(int i=head[x]; i; i=nxt[i]) {int y=to[i];if(y==f)continue;dfs(y,x);}id[++cnt]=x;//結束時間out[x]=cnt;
}
//……

3. DFS 序的應用

3.1 割點

什么是割點？

如果去掉一個節點以及與它連接的邊，該點原來所在的圖被分成兩部分，則稱該點為割點。如下圖所示，刪除 2號節點，剩下的節點之間就不能兩兩相互到達了。例如 4號不能到5號，6號也不能到達1號等等。一個連通分量變成兩個連通分量！

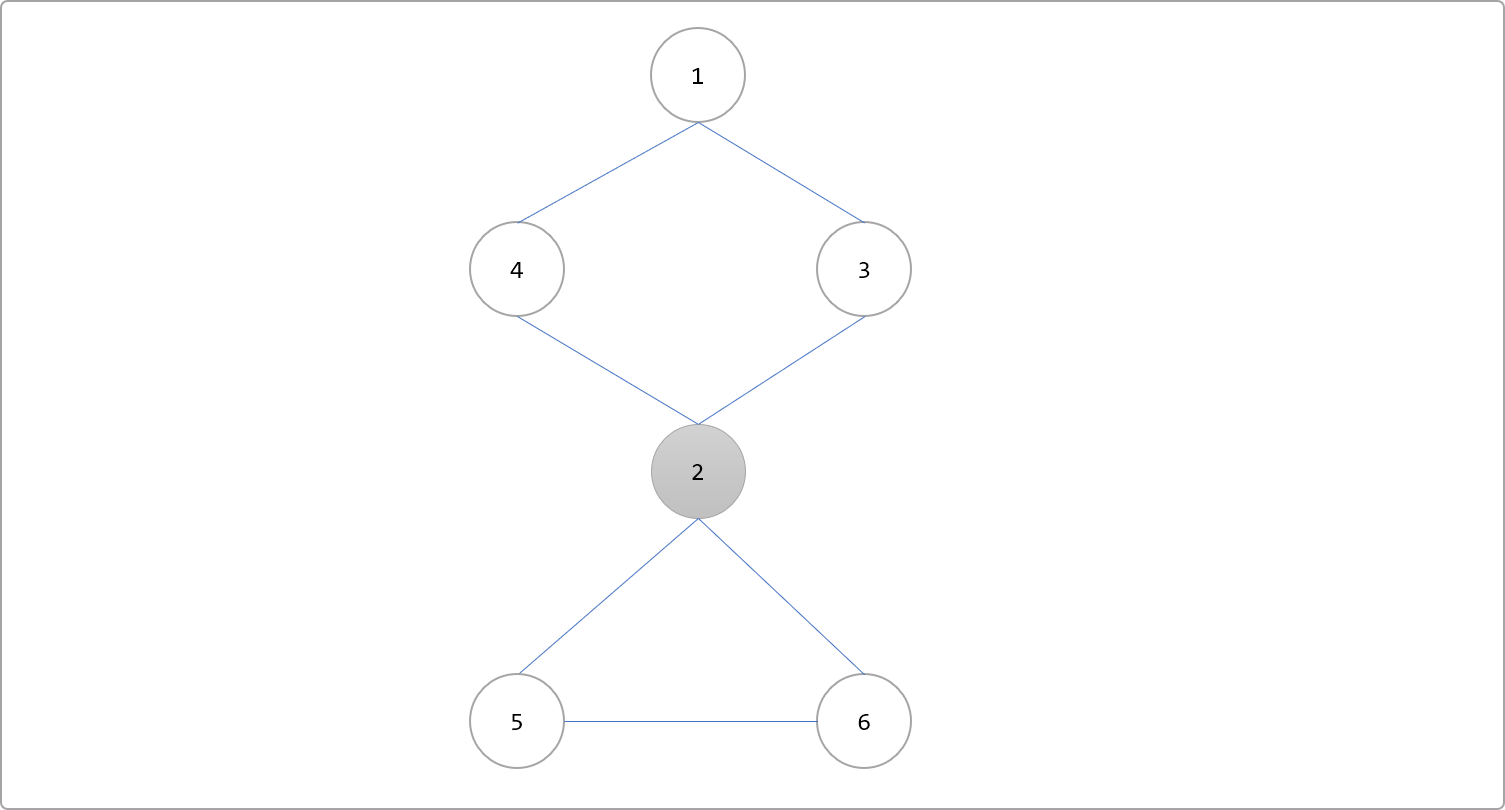
怎么判斷圖是否存在割點以及如何找出圖的割點？

Tarjan 算法是圖論中非常實用且常用的算法之一，能解決強連通分量、雙連通分量、割點和割邊（橋）、求最近公共祖先（LCA）等問題。

Tarjan算法求解割點的核心理念：

在深度優先遍歷算法訪問到k點時，此時圖會被k點分割成已經被訪問過的點和沒有被訪問過的點。
如果k點是割點，則沒有被訪問過的點中至少會有一個點在不經過k點的情況下，是無論如何再也回不到已訪問過的點了。則可證明k點是割點。

下圖是深度優先遍歷訪問到2號頂點的時候。沒有被訪問到的頂點有4、5、6號頂點。

Tips： 節點邊上的數字表示時間戳。

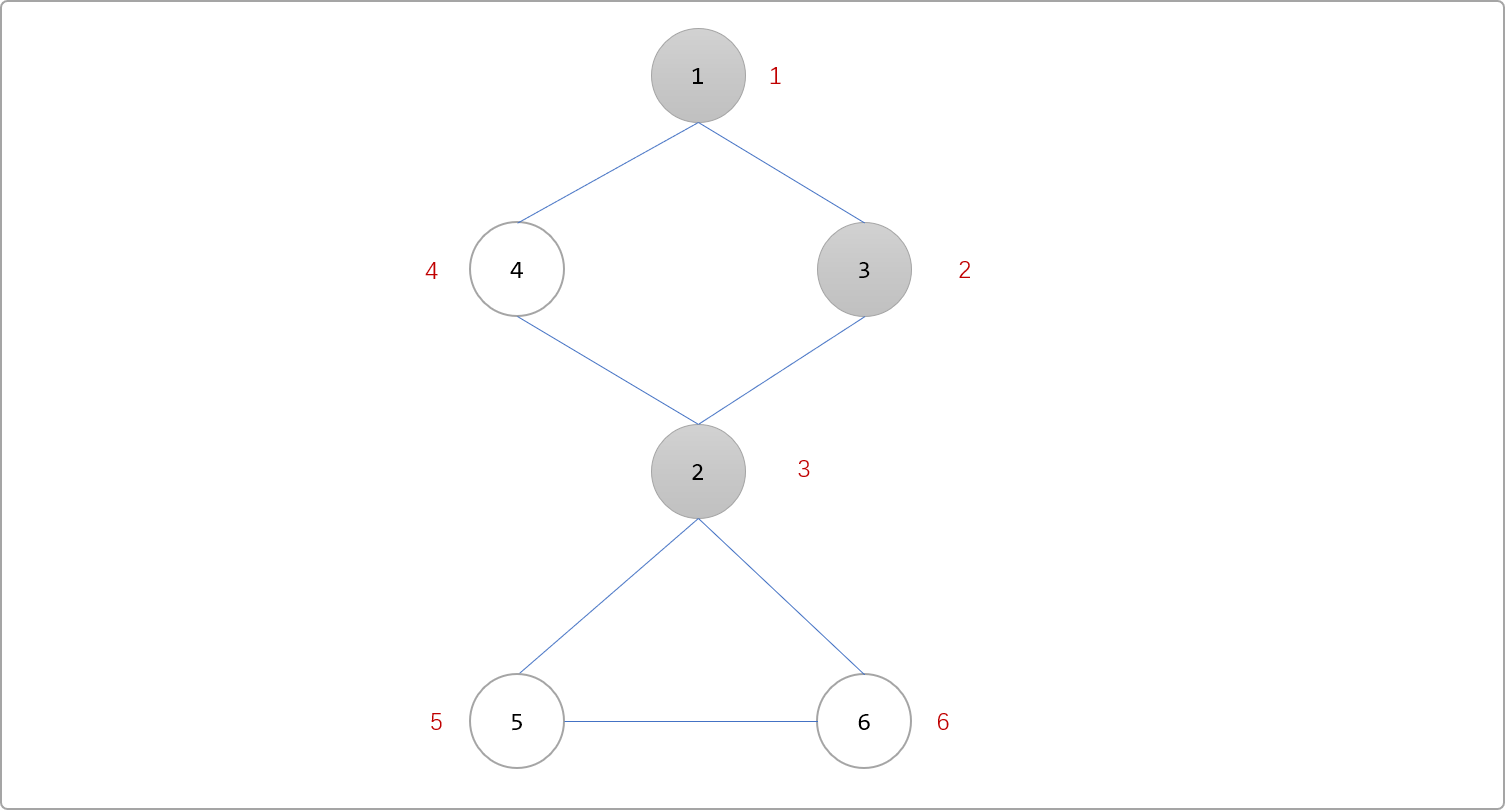
其中5和6號頂點都不可能在不經過2號頂點的情況下，再次回到已被訪問過的頂點(1和3號頂點)，因此2號頂點是割點。

問題變成如何在深度搜索到 k點時判斷，沒有被訪問過的點是否能通過此k或者不能通過此k點回到曾經訪問過的點。

算法中引入了回溯值概念。

回溯值表示從當前節點能回訪到時間戳最小的祖先，回溯值一般使用名為 low的數組存儲，low[i]表示節點 i的回溯值。

如下演示如何初始化以及更新節點的 low值。

定義3 個數組。vis[i]記錄節點是否訪問過、dfn[i]記錄節點的時間戳、low[i]記錄節點的回溯值。如下圖所示，從 1號節點開始深搜，搜索到4號節點時，3個數組中的值的變化如下。也就是說，初始，節點的 low值和dfn值相同。或者說此時，回溯值還不能確定。

Tips：注意一個細節，由1->3，認為 1是3的父節點。

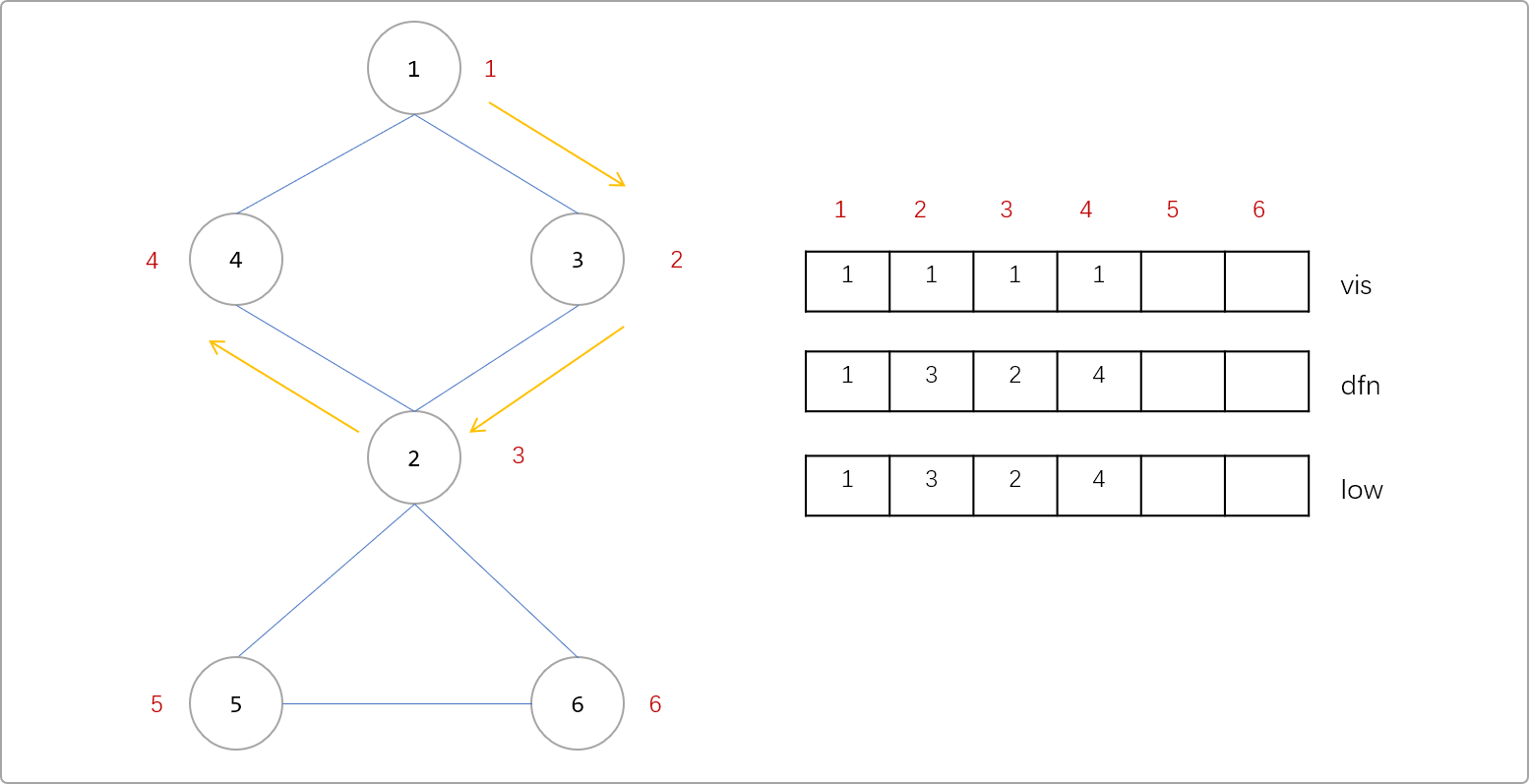
搜索到4號時，與4號相連的邊有4->1，4->1是沒有訪問過的邊，且1號節點已經標記過訪問過，也就是說通過4號點又回到了1號點。所以說4->1是一條回邊，或者說 1-……-4之間存在一個環。則4號點的 low[4]=min( low[4],dfn[1] )=1

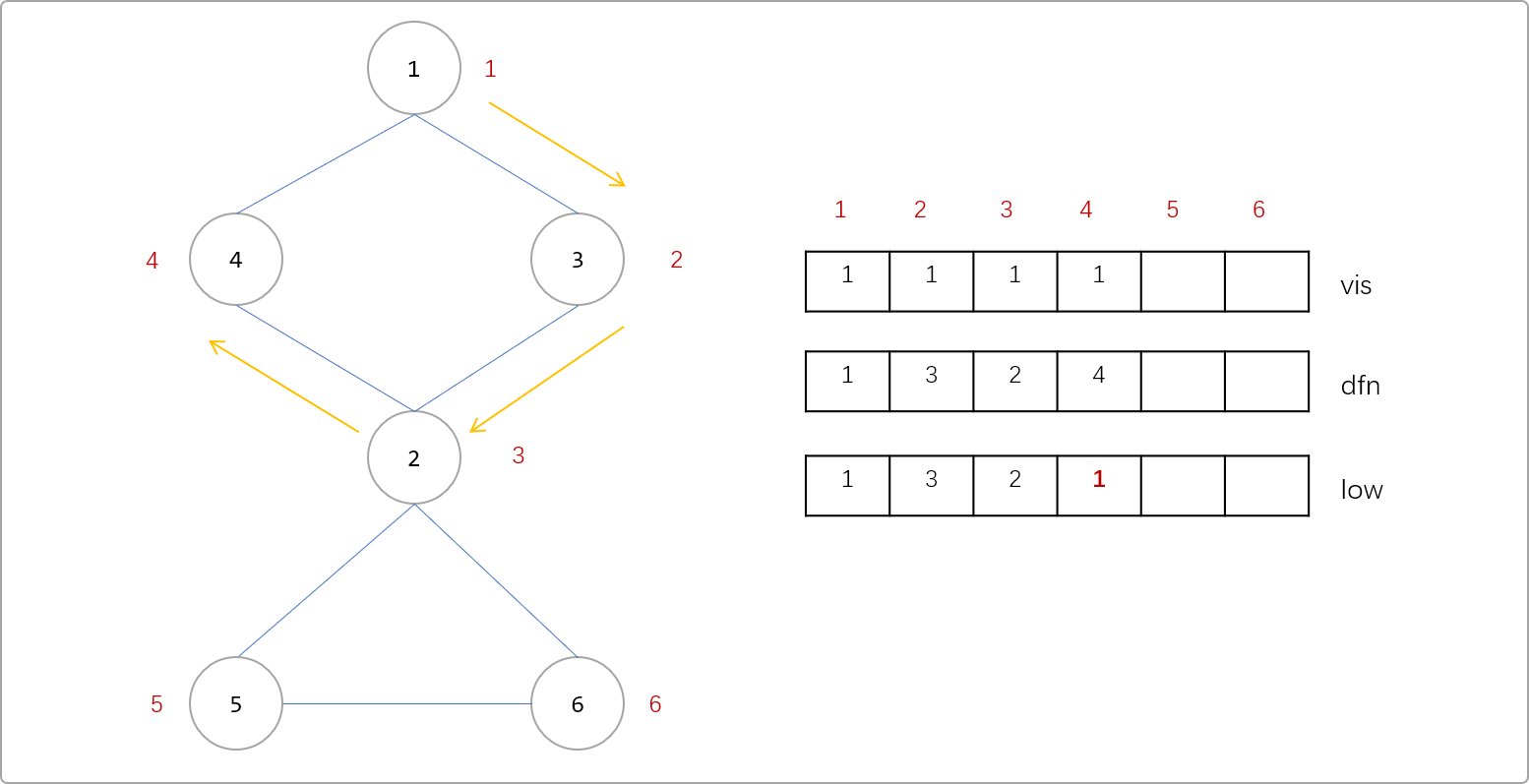
因為 2是4的父節點，顯然也是能通過4號點回到1號點，所以也需要更新其low值，更新表達式為 low[2]=min(low[2],low[4])。同理3號點是2號點的父節點，也能通過 3->2->4->1回到1號點。所以3號點的low也需要更新。low[3]=min(low[2],low[3])。

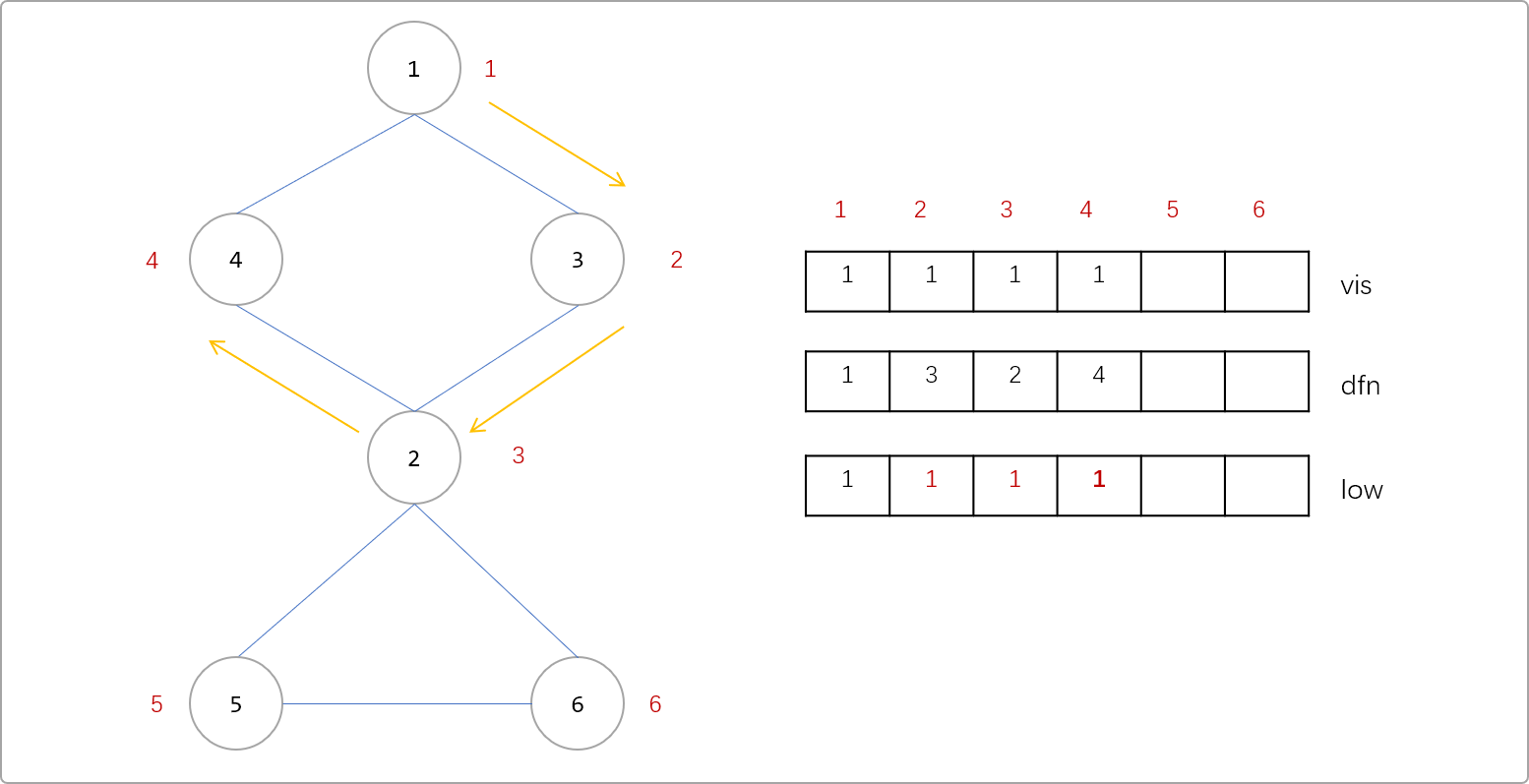
繼續更新5、6號節點的low值。

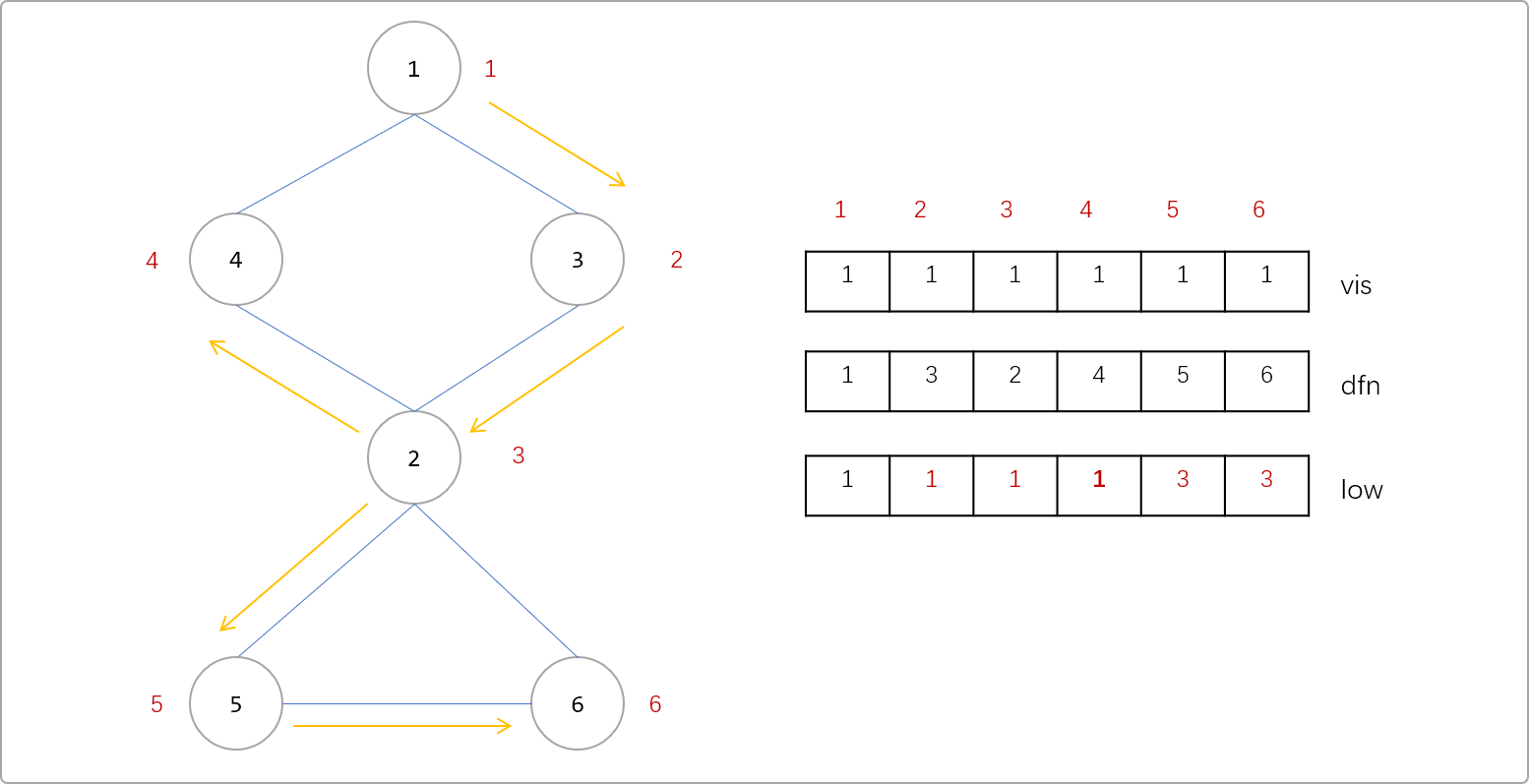
根據這些信息，如何判斷割點。

如果當前點為根節點時，若子樹數量大于一，則說明該點為割點（子樹數量不等于與該點連接的邊數）。
如果當前點不為根節點，若存在一個兒子節點的low值大于或等于該點的dfn值時（low[子節點] >= dfn[父節點]），該點為割點（即子節點，無法通過回邊，到達某一部分節點（這些節點的dfn值小于父親節點））。這個道理是很好理解的，說明子節點想重回樹的根節點是無法繞開父節點。

3.2 割邊

定義：即在一個無向連通圖中，如果刪除某條邊后，圖不再連通。如下圖刪除2-5和5-6后，圖不再具有連通性。

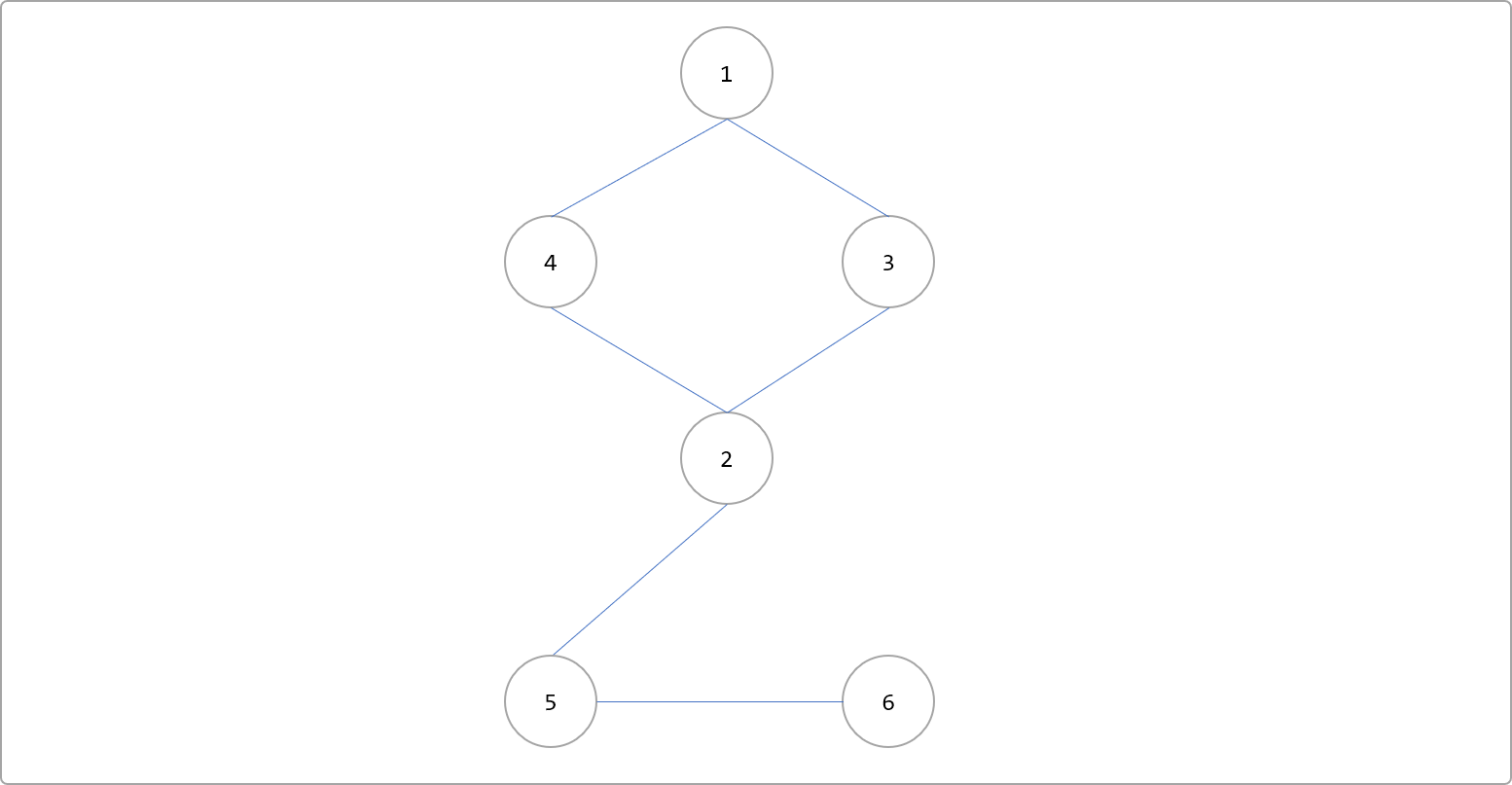
刪除2-5和5-6邊后。

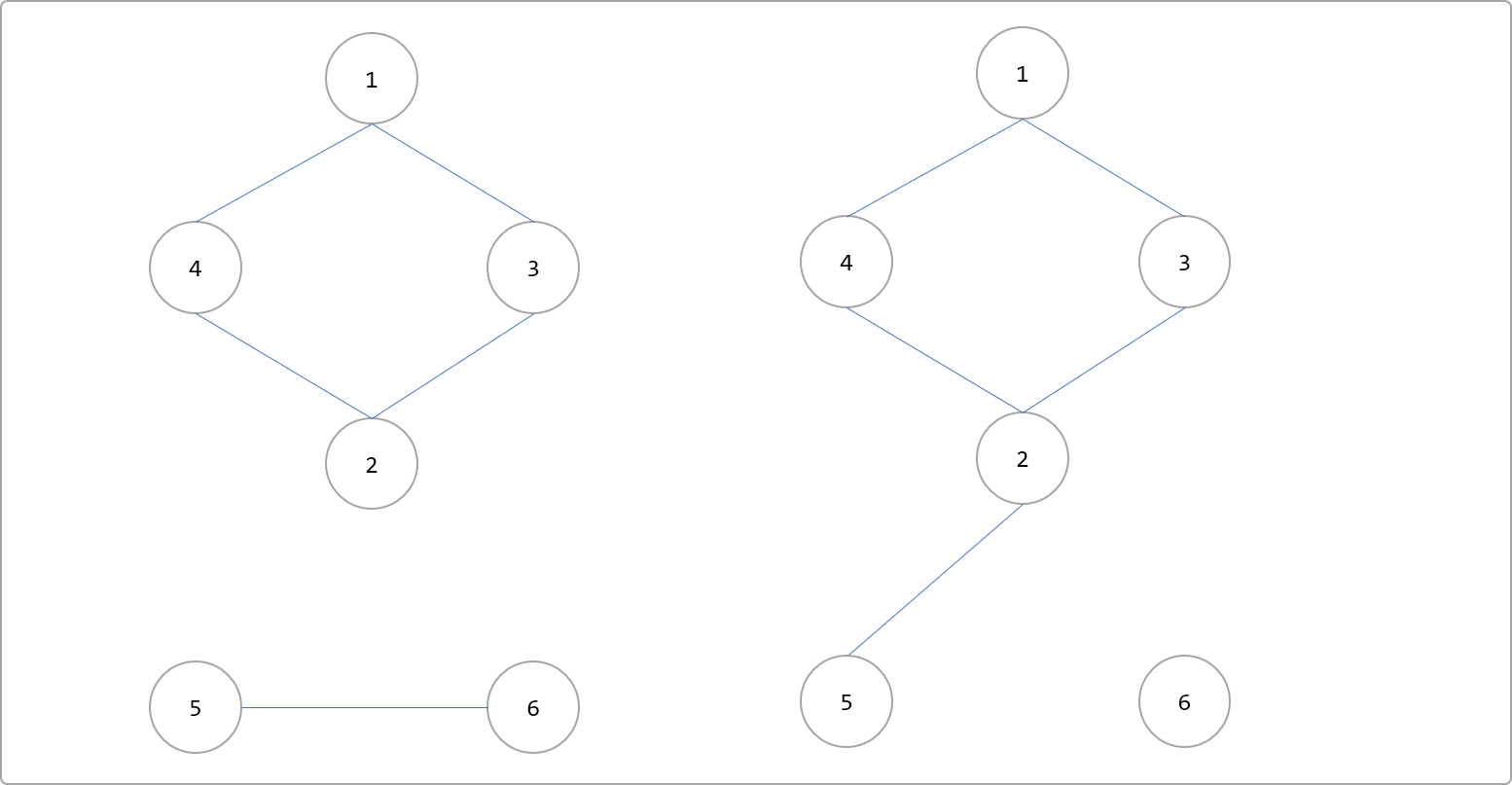
那么如何求割邊呢？

只需要將求割點的算法修改一個符號就可以。只需將low[v]>=num[u]改為low[v]>num[u]，取消一個等于號即可。因為low[v>=num[u]代表的是點v 是不可能在不經過父親結點u而回到祖先（包括父親）的，所以頂點u是割點。

如果low[y]和num[x]相等則表示還可以回到父親，而low[v]>num[u]則表示連父親都回不到了。倘若頂點v不能回到祖先，也沒有另外一條路能回到父親，那么 w-v這條邊就是割邊，

3.3 `Tarjan` 算法

#include <iostream>
#include <string.h>
#include <string>
#include <algorithm>
#include <math.h>
#include <vector>
using namespace std;
const int maxn = 123456;
int n, m, dfn[maxn], low[maxn], vis[maxn], ans, tim;bool cut[maxn];
vector<int> edge[maxn];void cut_bri(int cur, int pop) {vis[cur] = 1;// 1表示正在訪問中dfn[cur] = low[cur] = ++tim;int children = 0; //子樹數量for (int i : edge[cur]) { //對于每一條邊if (i == pop || vis[cur] == 2)continue;if (vis[i] == 1) //遇到回邊low[cur] = min(low[cur], dfn[i]); //回邊處的更新 (有環)if (vis[i] == 0) {cut_bri(i, cur);children++;  //記錄子樹數目low[cur] = min(low[cur], low[i]); //父子節點處的回溯更新if ((pop == -1 && children > 1) || (pop != -1 && low[i] >= dfn[cur])) { //判斷割點if (!cut[cur])ans++;   //記錄割點個數cut[cur] = true; //處理割點}if(low[i]>dfn[cur]) { //判斷割邊edge[cur][i]=edge[i][cur]=true;  //low[i]>dfn[cur]即說明(i,cur)是橋(割邊)；}}}vis[cur] = 2; //標記已訪問
}
int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= m; i++) {int x, y;scanf("%d%d", &x, &y);edge[x].push_back(y);edge[y].push_back(x);}for (int i = 1; i <= n; i++) {if (vis[i] == 0)cut_bri(i, -1); //防止原來的圖并不是一個連通塊//對于每個連通塊調用一次cut_bri}printf("%d\n", ans);for (int i = 1; i <= n; i++) //輸出割點if (cut[i])printf("%d ", i);return 0;
}

4.歐拉序

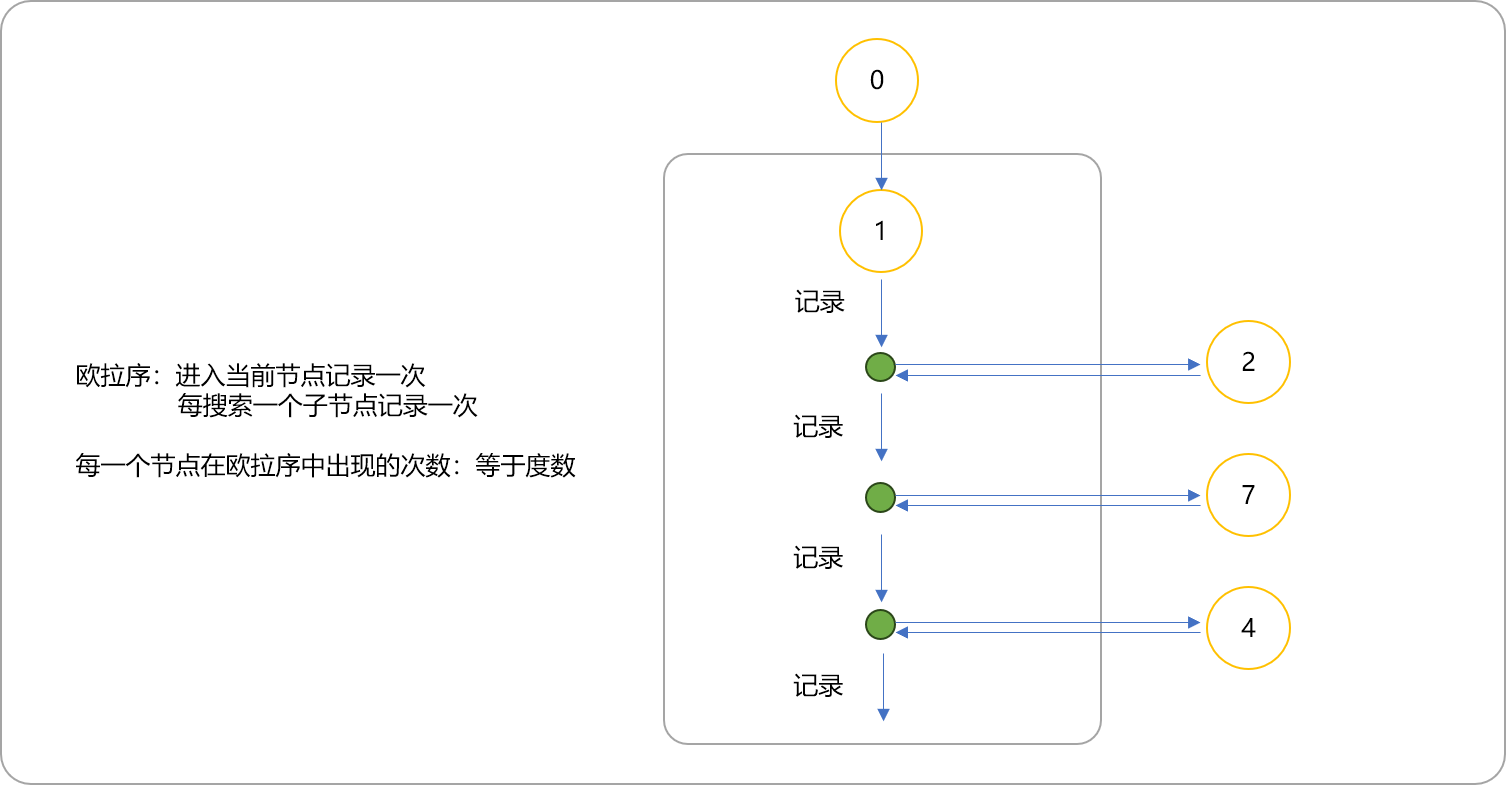
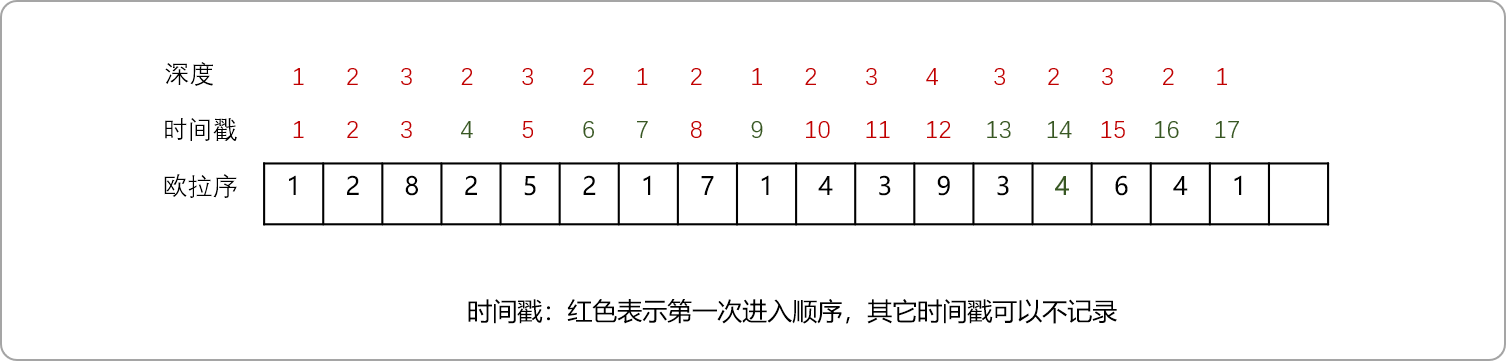
定義：進入節點時記錄，每次遍歷完一個子節點時，返回到此節點記錄，得到的 2 ? N ? 1 長的序列；

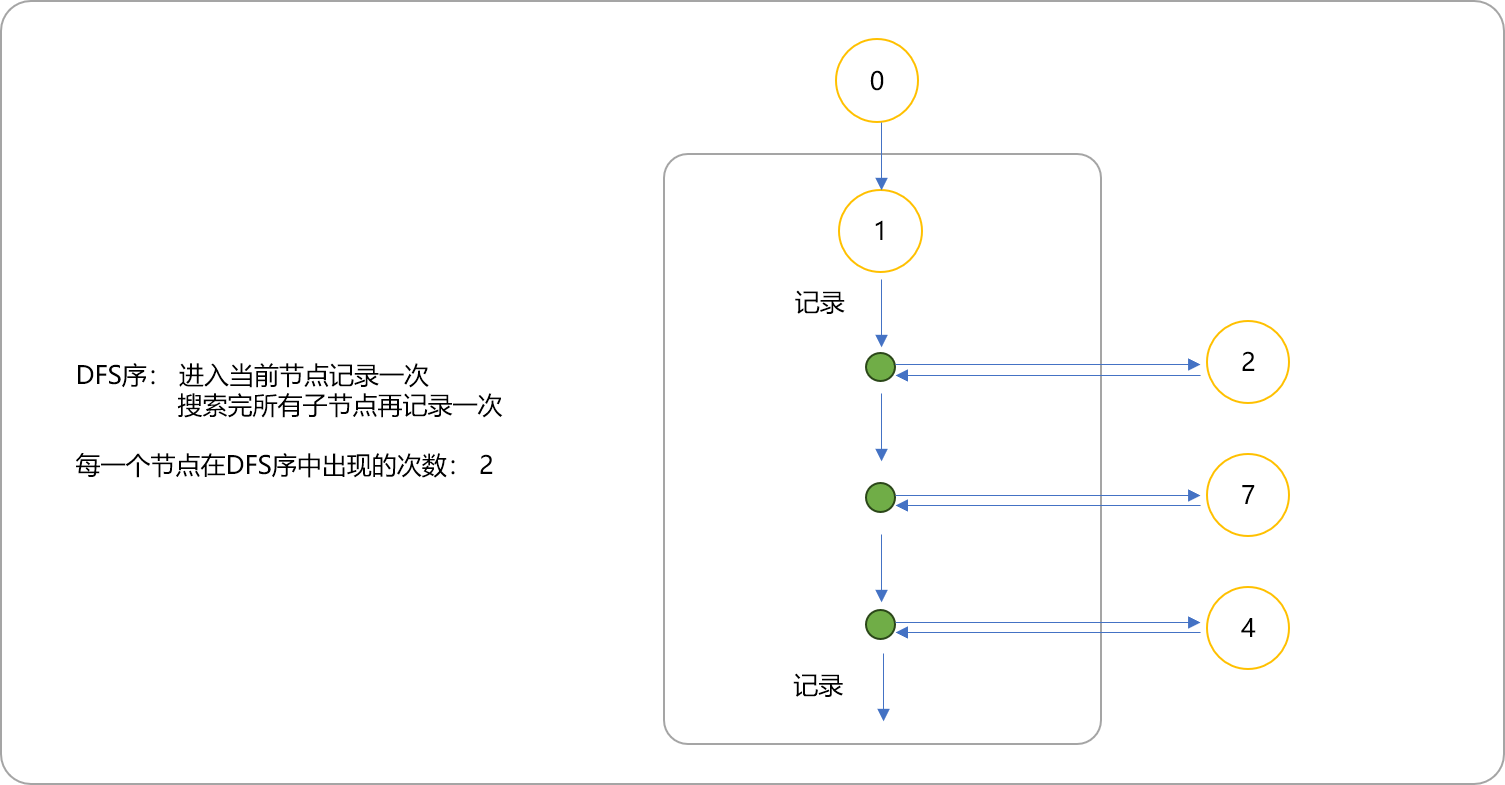
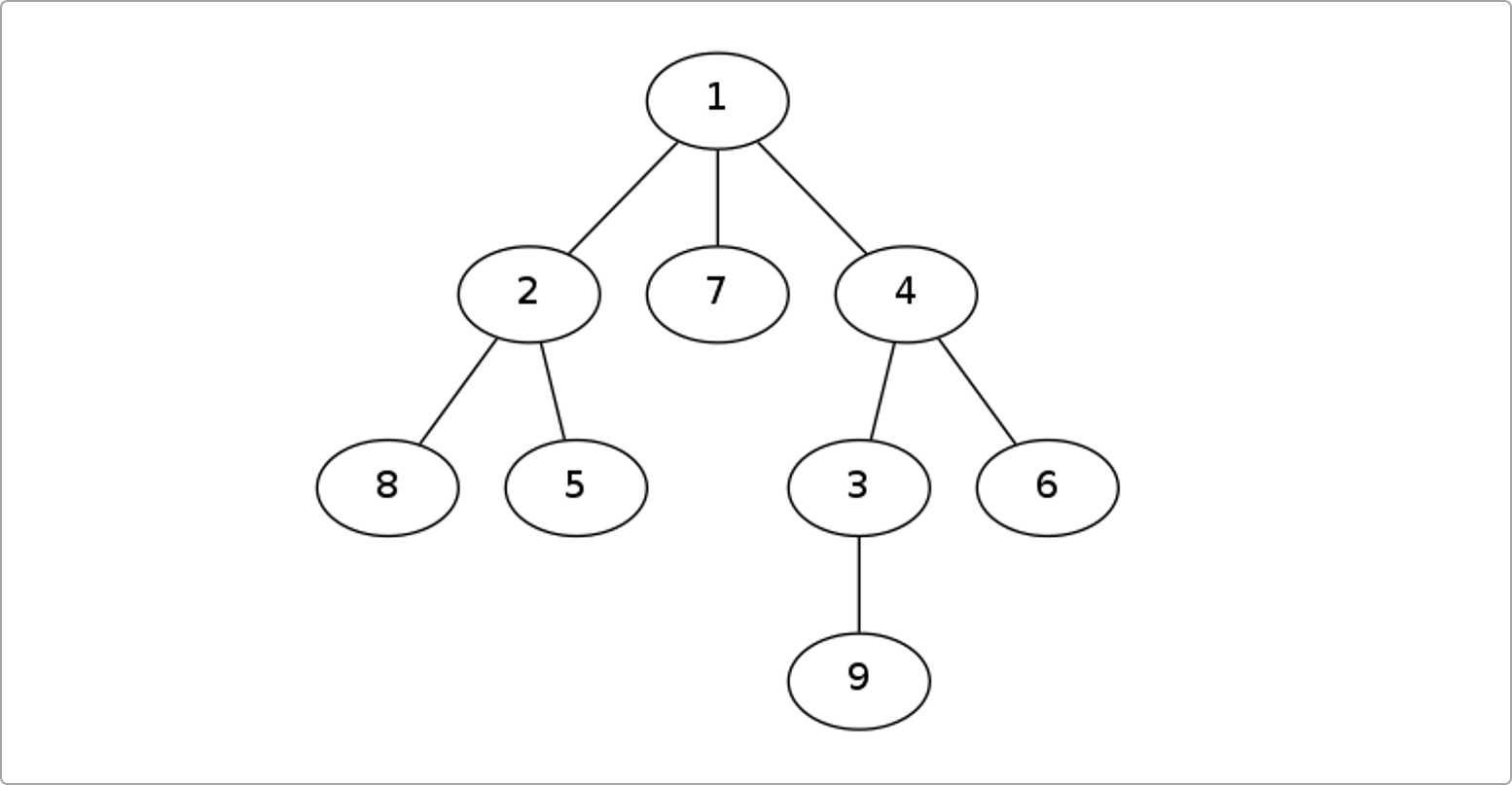
歐拉序和DFS序的區別，前者在每一個子節點訪問后都要記錄自己，后者只需要訪問完所有子節點后再記錄一次。如下圖的歐拉序就是：
1 2 8 2 5 2 1 7 1 4 3 9 3 4 6 4 1。每個點在歐拉序中出現的次數等于這個點的度數，因為DFS到的時候加進一次，回去的時候也加進。

性質：

節點 x 第一次出現與最后一次出現的位置之間的節點均為 x 的子節點；
任意兩個節點的 LCA 是歐拉序中兩節點第一次出現位置中深度最小的節點。兩個節點第一次出現的位置之間一定有它們的LCA，并且，這個LCA一定是這個區間中深度最小的點。

根據歐拉序的性質，可以用來求解CLA。如上圖，求解 LCA(9,6)。

在歐拉序中找到9和6第一次出現的位置。

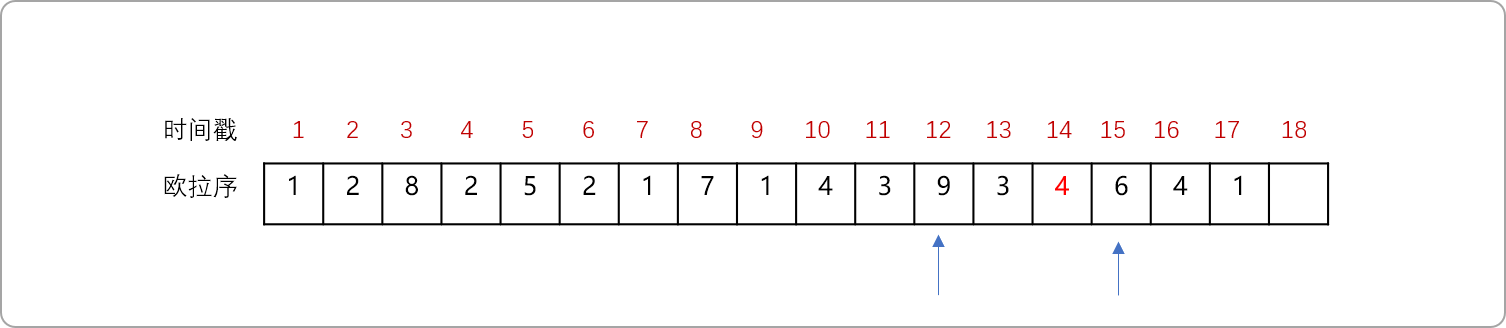
直觀比較，知道4號節點是其LCA，特征是9和6之間深度最小的節點。

歐拉序求LCA，先求圖的歐拉序、時間戳（可以記錄進入和離開節點的時間）以及節點深度。有了這些信息，理論上足以求出任意兩點的LCA。變成了典型的RMQ問題。

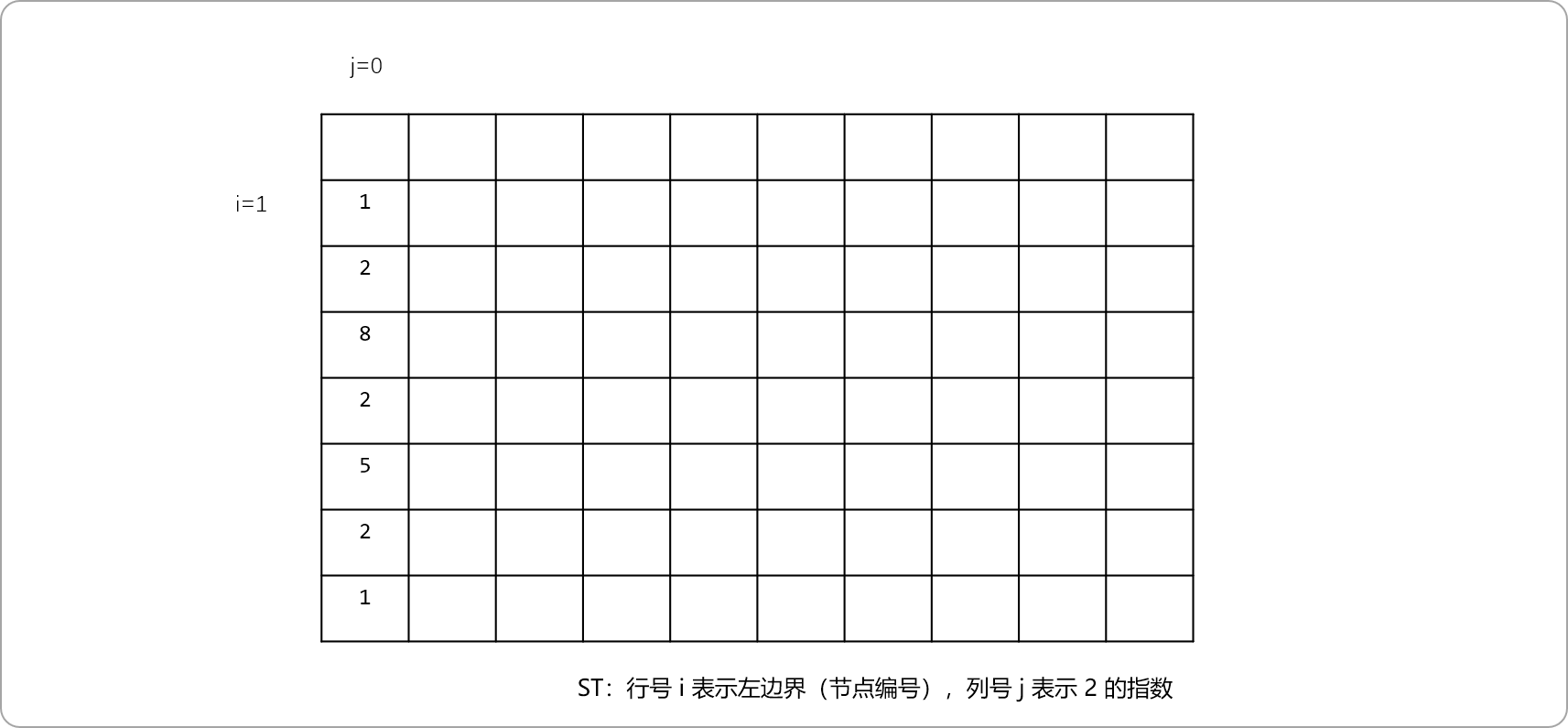
為了提升多次查詢性能，可以使用ST表根據節點的深度緩存節點的信息。j=0時如下圖所示。

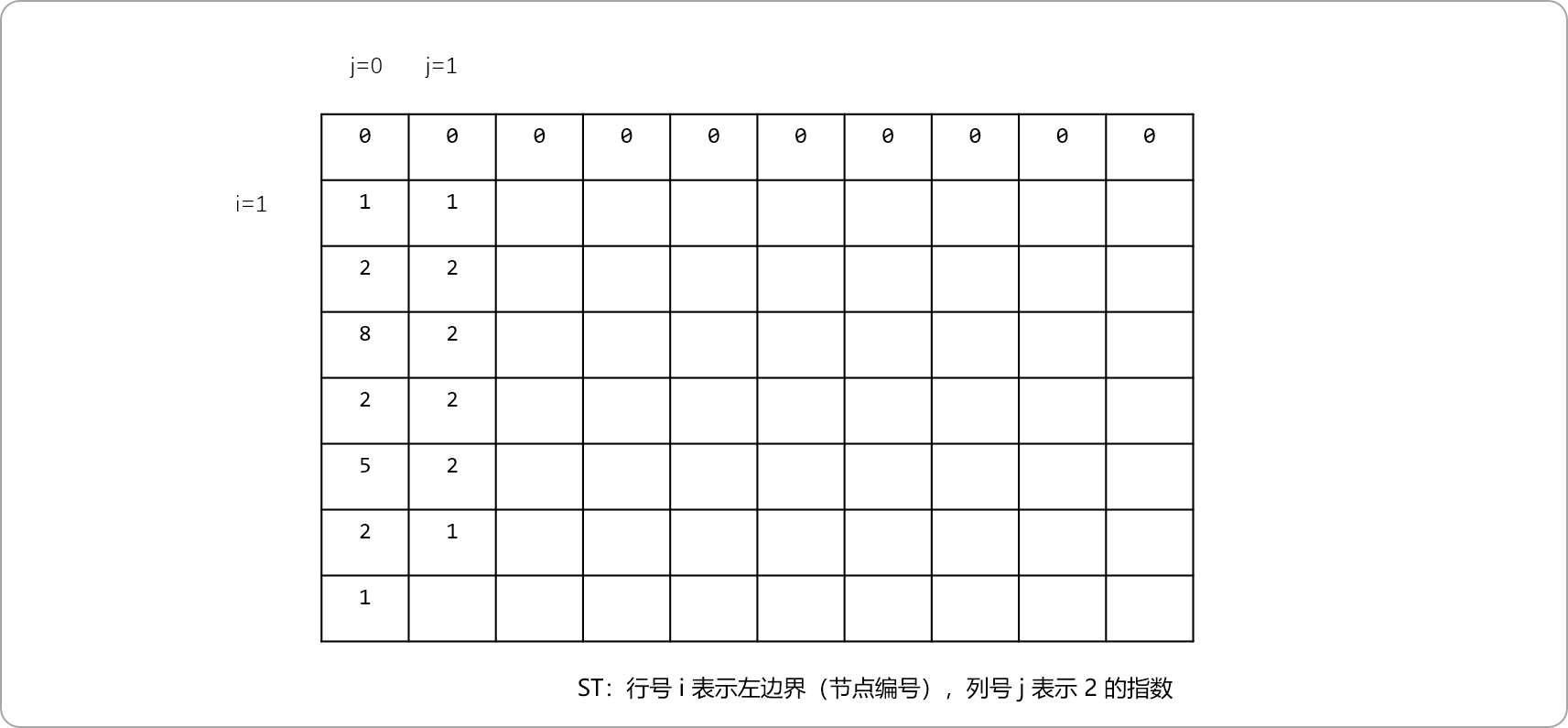
j=1表示區間長度為 2，值為區間長度為 1的兩個子區間的深度值小的節點。

歐拉序求LCA

#include <iostream>
#include <string.h>
#include <string>
#include <algorithm>
#include <math.h>
#include <vector>
using namespace std;
const int maxn = 10000;
int n, m, dfn[maxn], dep[maxn], tim;
int ol[maxn];
int st[maxn][maxn],lg2[maxn];
vector<int> edge[maxn];
void dfs(int cur, int fa) {ol[++tim]=cur;dfn[cur]=tim;dep[cur]=dep[fa]+1;for (int v : edge[cur]) { //對于每一條邊if(v==fa)continue;dfs(v,cur);ol[++tim]=cur;}
}void stPreprocess() {lg2[0] = -1;  // 預處理 lg 代替庫函數 log2 來優化常數for (int i = 1; i <= (n << 1); ++i) {lg2[i] = lg2[i >> 1] + 1;}for (int i = 1; i <= (n << 1) - 1; ++i) {st[i][0] = ol[i];}for (int j = 1; j <= lg2[(n << 1) - 1]; ++j) {for (int i = 1; i + (1 << j) - 1 <= ((n << 1) - 1); ++i) {st[i][j] = dep[ st[i] [ j - 1 ] ] < dep[ st[ i + (1 << j - 1)][j - 1 ]    ]  ? st[i][j - 1 ] : st[ i + (1 << j - 1)][j - 1 ];}cout<<endl;}
}int getlca(int u, int v) {if(dfn[u]>dfn[v])swap(u,v);u=dfn[u],v=dfn[v];int d=lg2[v-u+1];int f1=st[ u ][d  ];int f2=st[v-(1<<d)+1 ][ d ];return dep[f1]<dep[f2]?f1:f2;
}int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= m; i++) {int x, y;scanf("%d%d", &x, &y);edge[x].push_back(y);edge[y].push_back(x);}dfs(1, 0);for (int i = 1; i <= 2*n-1; i++) //輸出割點printf("%d-%d  ", ol[i],dfn[ ol[i] ]);stPreprocess();int u,v;cin>>u>>v;int res=getlca(u,v);cout<< res;return 0;
}