基于C#實現線段樹

一、線段樹

線段樹又稱"區間樹”，在每個節點上保存一個區間，當然區間的劃分采用折半的思想，葉子節點只保存一個值，也叫單元節點，所以最終的構造就是一個平衡的二叉樹，擁有 CURD 的 O(lgN)的時間。

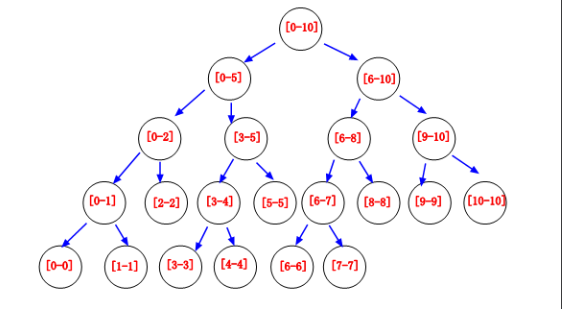
從圖中我們可以清楚的看到[0-10]被劃分成線段的在樹中的分布情況，針對區間[0-N]，最多有 2N 個節點，由于是平衡二叉樹的形式也可以像堆那樣用數組來玩，不過更加耗費空間，為最多 4N 個節點，在針對 RMQ 的問題上，我們常常在每個節點上增加一些 sum，max，min 等變量來記錄求得的累加值，當然你可以理解成動態規劃的思想，由于擁有 logN 的時間，所以在 RMQ 問題上比數組更加優美。

二、代碼

1、在節點中定義一些附加值，方便我們處理 RMQ 問題。

 #region 線段樹的節點/// <summary>/// 線段樹的節點/// </summary>public class Node{/// <summary>/// 區間左端點/// </summary>public int left;/// <summary>/// 區間右端點/// </summary>public int right;/// <summary>/// 左孩子/// </summary>public Node leftchild;/// <summary>/// 右孩子/// </summary>public Node rightchild;/// <summary>/// 節點的sum值/// </summary>public int Sum;/// <summary>/// 節點的Min值/// </summary>public int Min;/// <summary>/// 節點的Max值/// </summary>public int Max;}#endregion

2、構建(Build)
前面我也說了，構建有兩種方法，數組的形式或者鏈的形式，各有特點，我就采用后者，時間為 O(N)。

  #region 根據數組構建“線段樹"/// <summary>/// 根據數組構建“線段樹"/// </summary>/// <param name="length"></param>public Node Build(int[] nums){this.nums = nums;return Build(nodeTree, 0, nums.Length - 1);}#endregion#region 根據數組構建“線段樹"/// <summary>/// 根據數組構建“線段樹"/// </summary>/// <param name="left"></param>/// <param name="right"></param>public Node Build(Node node, int left, int right){//說明已經到根了，當前當前節點的max，sum，min值（回溯時統計上一層節點區間的值）if (left == right){return new Node{left = left,right = right,Max = nums[left],Min = nums[left],Sum = nums[left]};}if (node == null)node = new Node();node.left = left;node.right = right;node.leftchild = Build(node.leftchild, left, (left + right) / 2);node.rightchild = Build(node.rightchild, (left + right) / 2 + 1, right);//統計左右子樹的值(min，max，sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;return node;}#endregion

3、區間查詢
在線段樹中，區間查詢還是有點小麻煩的，存在三種情況。
① 完全包含：也就是節點的線段范圍完全在查詢區間的范圍內，這說明我們要么到了“單元節點",要么到了一個子區間，這種情況就是我找到了查詢區間的某一個子區間，直接累積該區間值就可以了。
② 左交集：這種情況我們需要到左子樹去遍歷。
③ 右交集：這種情況我們需要到右子樹去遍歷。
比如說：我要查詢 Sum[4-8]的值,最終會成為:Sum 總=Sum[4-4]+Sum[5-5]+Sum[6-8]，時間為 log(N)。

 #region 區間查詢/// <summary>/// 區間查詢(分解)/// </summary>/// <returns></returns>public int Query(int left, int right){int sum = 0;Query(nodeTree, left, right, ref sum);return sum;}/// <summary>/// 區間查詢/// </summary>/// <param name="left">查詢左邊界</param>/// <param name="right">查詢右邊界</param>/// <param name="node">查詢的節點</param>/// <returns></returns>public void Query(Node node, int left, int right, ref int sum){//說明當前節點完全包含在查詢范圍內，兩點：要么是單元節點，要么是子區間if (left <= node.left && right >= node.right){//獲取當前節點的sum值sum += node.Sum;return;}else{//如果當前的left和right 和node的left和right無交集，此時可返回if (node.left > right || node.right < left)return;//找到中間線var middle = (node.left + node.right) / 2;//左孩子有交集if (left <= middle){Query(node.leftchild, left, right, ref sum);}//右孩子有交集if (right >= middle){Query(node.rightchild, left, right, ref sum);}}}#endregion

4、更新操作
這個操作跟樹狀數組中的更新操作一樣，當遞歸的找到待修改的節點后，改完其值然后在當前節點一路回溯，并且在回溯的過程中一路修改父節點的附加值直到根節點，至此我們的操作就完成了，復雜度同樣為 logN。

 #region 更新操作/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(int index, int key){Update(nodeTree, index, key);}/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(Node node, int index, int key){if (node == null)return;//取中間值var middle = (node.left + node.right) / 2;//遍歷左子樹if (index >= node.left && index <= middle)Update(node.leftchild, index, key);//遍歷右子樹if (index <= node.right && index >= middle + 1)Update(node.rightchild, index, key);//在回溯的路上一路更改，復雜度為lgNif (index >= node.left && index <= node.right){//說明找到了節點if (node.left == node.right){nums[index] = key;node.Sum = node.Max = node.Min = key;}else{//回溯時統計左右子樹的值(min，max，sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;}}}#endregion

最后我們做個例子，在 2000000 的數組空間中，尋找 200-3000 區間段的 sum 值，看看他的表現如何。

 using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Diagnostics;using System.Threading;using System.IO;namespace ConsoleApplication2{public class Program{public static void Main(){int[] nums = new int[200 * 10000];for (int i = 0; i < 10000 * 200; i++){nums[i] = i;}Tree tree = new Tree();//將當前數組構建成 “線段樹”tree.Build(nums);var watch = Stopwatch.StartNew();var sum = tree.Query(200, 3000);watch.Stop();Console.WriteLine("耗費時間:{0}ms,  當前數組有:{1}個數字, 求出Sum=:{2}", watch.ElapsedMilliseconds, nums.Length, sum);Console.Read();}}public class Tree{#region 線段樹的節點/// <summary>/// 線段樹的節點/// </summary>public class Node{/// <summary>/// 區間左端點/// </summary>public int left;/// <summary>/// 區間右端點/// </summary>public int right;/// <summary>/// 左孩子/// </summary>public Node leftchild;/// <summary>/// 右孩子/// </summary>public Node rightchild;/// <summary>/// 節點的sum值/// </summary>public int Sum;/// <summary>/// 節點的Min值/// </summary>public int Min;/// <summary>/// 節點的Max值/// </summary>public int Max;}#endregionNode nodeTree = new Node();int[] nums;#region 根據數組構建“線段樹"/// <summary>/// 根據數組構建“線段樹"/// </summary>/// <param name="length"></param>public Node Build(int[] nums){this.nums = nums;return Build(nodeTree, 0, nums.Length - 1);}#endregion#region 根據數組構建“線段樹"/// <summary>/// 根據數組構建“線段樹"/// </summary>/// <param name="left"></param>/// <param name="right"></param>public Node Build(Node node, int left, int right){//說明已經到根了，當前當前節點的max，sum，min值（回溯時統計上一層節點區間的值）if (left == right){return new Node{left = left,right = right,Max = nums[left],Min = nums[left],Sum = nums[left]};}if (node == null)node = new Node();node.left = left;node.right = right;node.leftchild = Build(node.leftchild, left, (left + right) / 2);node.rightchild = Build(node.rightchild, (left + right) / 2 + 1, right);//統計左右子樹的值(min，max，sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;return node;}#endregion#region 區間查詢/// <summary>/// 區間查詢(分解)/// </summary>/// <returns></returns>public int Query(int left, int right){int sum = 0;Query(nodeTree, left, right, ref sum);return sum;}/// <summary>/// 區間查詢/// </summary>/// <param name="left">查詢左邊界</param>/// <param name="right">查詢右邊界</param>/// <param name="node">查詢的節點</param>/// <returns></returns>public void Query(Node node, int left, int right, ref int sum){//說明當前節點完全包含在查詢范圍內，兩點：要么是單元節點，要么是子區間if (left <= node.left && right >= node.right){//獲取當前節點的sum值sum += node.Sum;return;}else{//如果當前的left和right 和node的left和right無交集，此時可返回if (node.left > right || node.right < left)return;//找到中間線var middle = (node.left + node.right) / 2;//左孩子有交集if (left <= middle){Query(node.leftchild, left, right, ref sum);}//右孩子有交集if (right >= middle){Query(node.rightchild, left, right, ref sum);}}}#endregion#region 更新操作/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(int index, int key){Update(nodeTree, index, key);}/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(Node node, int index, int key){if (node == null)return;//取中間值var middle = (node.left + node.right) / 2;//遍歷左子樹if (index >= node.left && index <= middle)Update(node.leftchild, index, key);//遍歷右子樹if (index <= node.right && index >= middle + 1)Update(node.rightchild, index, key);//在回溯的路上一路更改，復雜度為lgNif (index >= node.left && index <= node.right){//說明找到了節點if (node.left == node.right){nums[index] = key;node.Sum = node.Max = node.Min = key;}else{//回溯時統計左右子樹的值(min，max，sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;}}}#endregion}}