/目·錄/

一、線性運算的光學實現

1.1.?光學矩陣乘法器

1.2.?光的衍射實現線性運行

1.3.?基于Rayleigh-Sommerfeld方程的實現方法

1.4.?基于傅立葉變換的實現

1.5.?通過光干涉實現線性操作

1.6.?光的散射實現線性運行

1.7.?波分復用（WDM）實現線性運行

二、非線性激活函數的光學實現

2.1. 非線性光學效應

2.2.?在光子神經網絡中實現非線性激活

三、發揮光電技術與人工智能結合的優勢

隨著大數據時代的到來，人工智能不斷受到各界關注，并在醫學圖像分析、分子與材料科學、語言識別等領域得到了廣泛應用。作為人工智能的基礎，神經網絡的研究成果令人矚目。

然而，由于電信號易受干擾、處理速度與能量損耗成正比等固有缺陷，研究人員將目光轉向了光，試圖在光學領域構建神經網絡，充分利用光的并行處理能力來解決電子神經網絡存在的問題。經過不斷的研究和發展，光神經網絡已經走在了科技研究的前列。

作為計算機科學中最活躍的領域之一，人工智能主要是通過構建人工神經網絡（ANN）來模擬神經系統的結構，建立神經網絡各層神經元之間的聯系，使其具有良好的泛化能力和魯棒性。自20世紀80年代以來，人工神經網絡的研究工作取得了長足的進步：在模式識別、智能機器人、自動控制、預測與估算、生物醫學、經濟等領域，成功地解決了許多現代計算機難以解決的實際問題，具有良好的智能特性。

目前，電子計算仍然是實現人工智能算法，尤其是在深度ANN模型最重要的計算力支撐。雖然具體的硬件架構各不相同，但總的來說，都是采用馮·諾依曼式計算原理，通過復雜的邏輯電路和處理器芯片來完成計算任務。

最初的神經網絡架構使用CPU進行計算，但無法滿足深度網絡中大量浮點運算的要求，尤其是訓練階段。而且并行計算效率太低，很快就被并行計算能力強的GPU所取代——可以說，GPU推動了深度學習的發展。

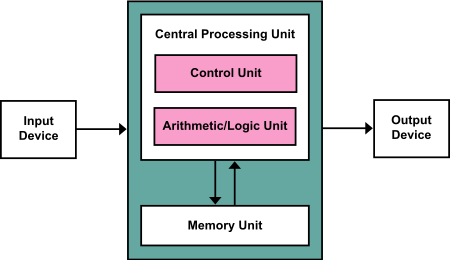
馮·諾依曼架構方案

然而，深度學習對計算能力的需求是無止境的。受限于電信號的干擾、能耗和物理限制，雖然現在以硅為基礎的電子元件還能支持，但傳統的深度學習已經悄然出現了瓶頸。學術界和工業界試圖尋求其他方法來解決電子缺陷，從而在計算能力上有所防范。由于光速高達每秒30萬公里，是電子速度的300倍，信息承載能力和種類是電通道的2*10^4倍，且并行性高、抗干擾性強，在信息傳輸和光計算方面具有巨大優勢。如今，以“光”代“電”已成為一種有潛力、有前景的工作模式，是時代發展的趨勢。

因此，人們嘗試用光的方式構建神經網絡，實現深度學習架構；光神經網絡（ONN）隨著時代的要求應運而生。它具有高帶寬、高互聯和內部并行處理的特點，可以加速軟件和電子硬件的部分運算，甚至達到“光速”，是一種很有希望取代人工神經網絡的方法。

在光子神經網絡中，矩陣乘法可以以光速進行，能有效解決人工神經網絡中的密集矩陣乘法，從而減少能量和時間的消耗。此外，人工神經網絡中的非線性也可以通過非線性光學元件來實現。一旦完成光神經網絡的訓練，整個結構就能以光速進行光信號計算，而無需額外的能量輸入。

1978年，斯坦福大學的古德曼（Joseph Goodman）首次提出了光矢量矩陣乘法器的理論模型，成為光計算領域的重要一步，并推動了光矩陣乘法器（OMM）和光子神經網絡的發展。

約瑟夫·古德曼

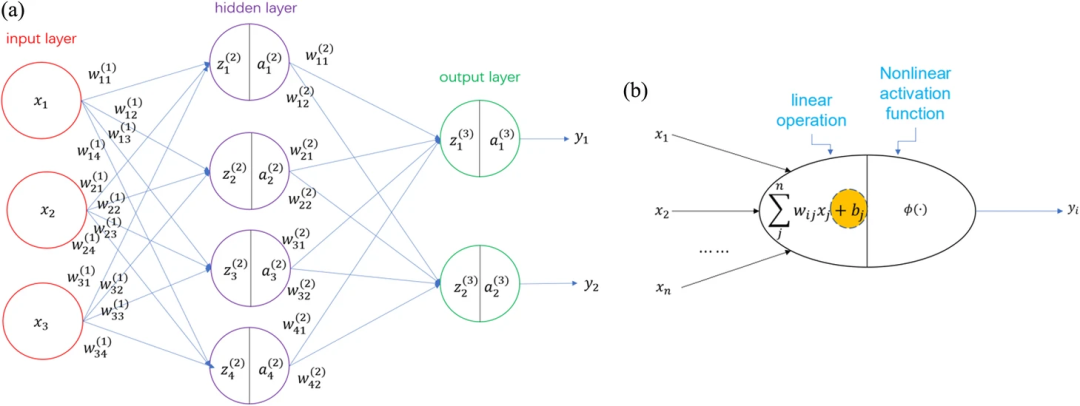
（a）ANN的結構；（b）神經元的原理

ONN是ANN線性和非線性運算的光學實現，神經網絡的結構和神經元的工作原理屬于線性運算zi = bi + ∑jWijxj 和非線性激活 ai = ?(zi)，因此，神經網絡需要大量的線性乘法運算和求和運算。

這種乘加運算在算法中最直接的體現就是給出兩組數據，在“for”循環中進行乘加運算。如果我們簡單地思考這個問題，就會發現完成這個運算需要多次迭代，會浪費大量的計算資源。因此，人們開始尋求一種更快的方法：矢量化方法，它可以將其轉化為兩個矩陣（即輸入矩陣和權重矩陣）的乘法運算。

我們知道，使用電子計算機很容易實現兩個矩陣之間的計算，但當矩陣維數非常大時也很難實現。并且，利用計算機實現乘法運算非常耗時。但是，如果利用光的高速度、高并行性和抗干擾性，通過光學手段實現這一運算，很可能只需要幾次運算，甚至只需要一次運算。在神經網絡的訓練中，我們需要處理和分析的數據極其龐大；此時，光學的特性就顯得極為重要，它可以為計算帶來極大的便利。光學矩陣乘法器的出現為光學計算奠定了基礎，也為神經網絡光學提供了發展路徑。

接下來，我們將簡要介紹光學矩陣乘法器，它是線性乘法和求和運算的基本光學實現方式——即矩陣乘法，然后從實現乘法運算的不同原理出發，說明如何在光學神經網絡中實現線性運算。

1）光學矩陣乘法器

矩陣乘法是矩陣運算中非常重要的運算，其計算過程比較復雜。簡單地說，兩個矩陣之間的乘法運算就是將第一個矩陣的第i行對應元素與第二個矩陣的第j列對應元素逐一相乘相加，得到結果矩陣元素cij，也稱為內積運算。

只需遍歷一次兩個矩陣的行或列，即可得到乘法結果矩陣。如果A = (aij)m × s，B = (bij)s × n，矩陣乘法運算定義如下：

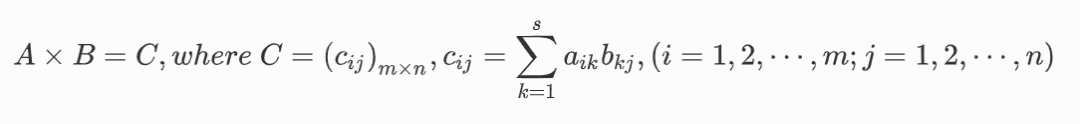
事實上，乘法是一個數字多次累加的過程；相應地，矩陣乘法就是多個不同數字經過多次累加后的和。在電子計算機中，累加器作為核心運算單元，可以用來實現矩陣乘法運算。同樣，這種光學乘法器也可以設計成光子計算系統的核心，具有二維并行性。光學乘法是光信息加載和轉換的過程，光學乘法器負責實現這一過程。

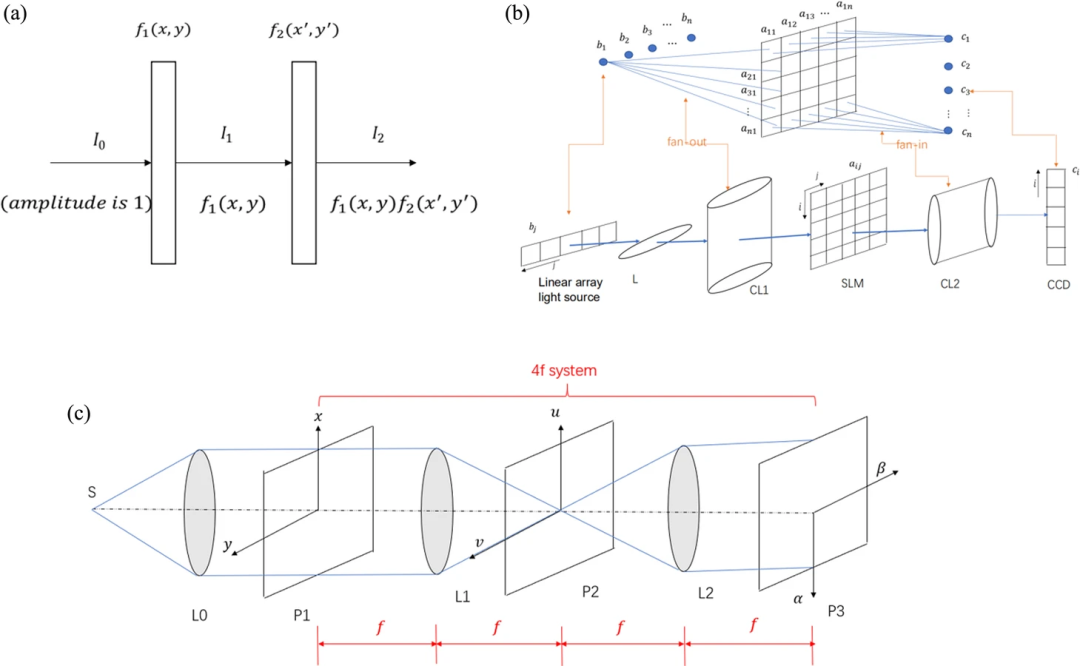
光學矩陣乘法器。（a）光學乘法器。（b）向量-矩陣乘法系統的結構。（c）4f系統實現的矩陣-矩陣乘法

光學矩陣乘法器充分體現了光的并行計算能力，OMM完成的光線性運算本質上是通過一定的方法和光的一些特性，如衍射、干涉等，進而實現對信息載體光的調制。

2）光的衍射實現線性運行

光在空氣中沿直線傳播。當遇到障礙物或小孔時，光就會偏離直線傳播路徑，從而產生光強分布不均勻的現象，這就是衍射。

1678年，荷蘭物理學家惠更斯（Christiaan Huygens）提出，波面上的每一點都可以看作是發射次級波的波源，分別發射球面次級波。在未來的某一時刻，這些次級波的包絡面將成為當時的新波面，這就是惠更斯原理。惠更斯原理雖然很好地解釋了光的折射、反射和雙折射現象，但并不涉及光波強度和波長的分析，不能很好地解釋衍射現象。

1810年楊氏雙光干涉實驗出現后，1815年菲涅爾（Augustin-Jean Fresnel）借助小波相干疊加對惠更斯原理進行了補充，將定性的惠更斯原理發展為具有數學證明的半定量原理，稱為惠更斯-菲涅爾原理，其表達式為：

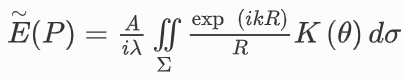
然而，該原理只是一個半定量原理，對于傾斜系數沒有具體的函數表示法，比例系數的含義也不明確，因此具有一定的局限性。

因此，基爾霍夫（Gustav Kirchhoff）和薩默菲爾德（Arnold Sommerfeld）根據一般波理論推導出了衍射公式，并給出了傾斜系數和比例系數的具體形式。基爾霍夫利用格林定理求解了亥姆霍茲方程，得到了自由空間中單色光的復振幅，最后總結出基爾霍夫積分定理，具體表達了惠更斯-菲涅爾原理的概念。基爾霍夫衍射公式如下?

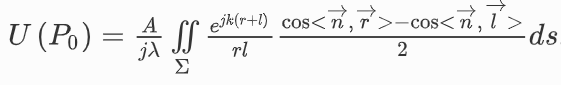
雖然基爾霍夫衍射公式具有良好的實際效果，但基爾霍夫假設的邊界條件違反了勢場定理。因此，薩默菲爾德采用了另一個格林公式來克服基爾霍夫邊界條件假設違反勢場定理的問題，使其在理論上自洽。這就是瑞利-索梅費爾德方程（Rayleigh-Sommerfeld equation），其具體形式表示為 ：

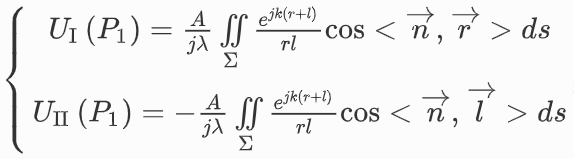
上述方程均基于菲涅耳衍射。此外，人們還發現了夫瑯禾費衍射，屬于遠場衍射。由于夫瑯禾費衍射場在理論上易于計算，具有很大的應用價值，而且在實驗上也不難實現，因此受到了人們更多的關注。特別是現代變換光學中傅立葉光學的興起，賦予了經典的夫瑯禾費衍射以新的現代光學意義。而隨著光學傅立葉變換的興起，實現了從空間域到頻率域的變換。光可以表示更多的內容，菲涅耳衍射中的光分布也得到了更詳細的分析。

3）基于Rayleigh-Sommerfeld方程的實現方法

任何障礙物都能引起光的衍射，但只有當障礙物或孔的尺寸小于或類似于光的波長時，才能觀察到明顯的衍射現象。

衍射會在小孔徑處產生許多小波。這些小波到達觀察屏時相互疊加。在疊加過程中，相互削弱的程度有規律地變輕或變重，從而形成明暗條紋。事實上，衍射是無限連續小波的相干疊加，在數學上表現為一個積分問題。因此，可以利用光衍射現象來設計光神經網絡的線性運算，實現神經網絡中的線性乘法運算和求和運算。

根據衍射理論的Rayleigh-Sommerfeld方程，我們可以將給定衍射層的每個神經元視為由光學模型組成的二次波源：這也是許多衍射網絡架構的基本原理。

利用光衍射實現線性運算的光學神經網絡。（a）深度衍射神經網絡D2NN示意圖。（b）衍射光柵網絡系統。（c）元表面實現光學邏輯運算

總之，基于Rayleigh-Sommerfeld方程的D2NN能夠以接近光速的速度完成傳統計算機神經網絡所能實現的各種復雜功能，而且不消耗能量。它為利用基于人工智能的無源元件快速分析數據、圖像和物體分類帶來了新的機遇，從而實現全光學圖像分析、特征檢測和物體分類。

例如，使用該技術的無人駕駛汽車可以立即對停車標志做出反應。只要接收到路牌衍射的光線，D2NN就能讀取路牌信息；該技術還可用于對大量目標進行分類，例如在數百萬個細胞樣本中尋找疾病跡象。

此外，利用D2NN執行任務的新型相機設計和光學元件可以被動地應用于醫療技術、機器人、安防以及任何需要圖像和視頻數據的應用中。例如，全光衍射神經網絡可用于構建全息圖像，通過三維打印以極低的成本實現“太赫茲”成像，高速重建高質量圖像。

4）基于傅立葉變換的實現

光的傅立葉變換也是衍射大家族中的一員，它是從弗勞恩霍夫衍射發展而來的，由于它的一些特殊性質，如卷積定理，在現代光學中發揮著極其重要的作用。

基于傅立葉光學，光學元件的傅立葉透鏡可以實現傅立葉變換，完成時域和頻域的轉換。根據卷積定理，空間域中兩個二維連續函數的卷積可以通過它們對應的兩個傅里葉變換乘積的逆變換得到。相反，頻域中的卷積可以通過空間域中乘積的傅里葉變換得到。因此，乘法運算可以通過頻域卷積，然后通過逆傅里葉變換來完成。

不僅如此，透鏡最簡單、最基本的功能之一就是匯聚光束，這在一定程度上類似于求和運算。因此，我們可以利用透鏡波的傅里葉變換和光波會聚疊加功能來實現光神經網絡的線性乘法功能和求和功能。

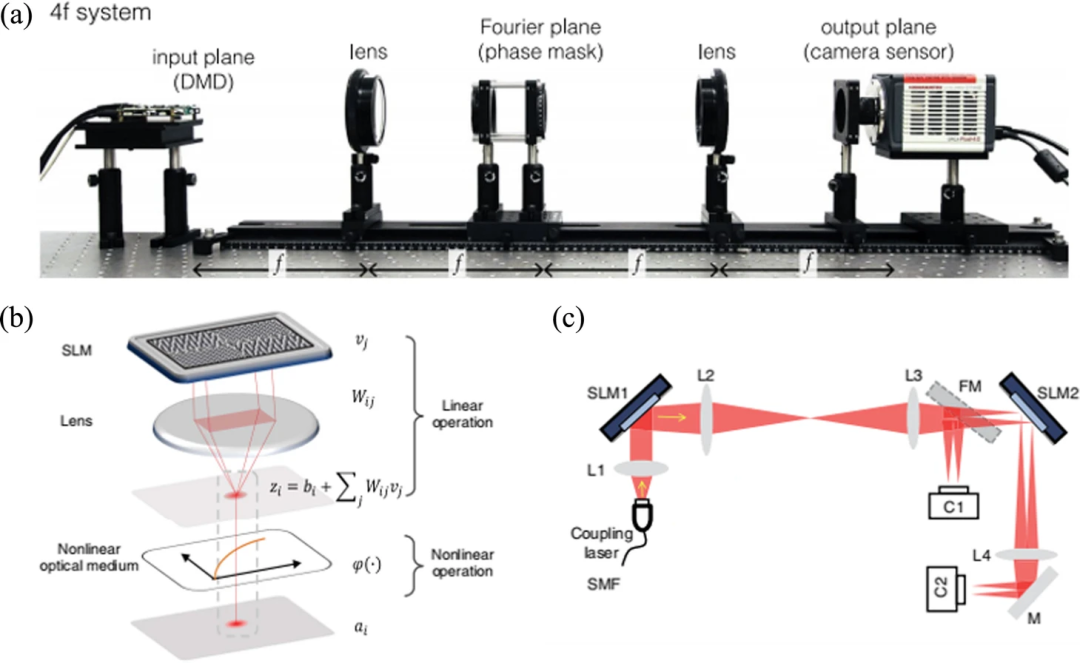
通過光的傅立葉變換實現線性操作的光神經網絡。（a）光卷積操作由4f系統實現；（b）光神經元在AONN中的實驗實現。（c）AONN的線性操作系統

5）通過光干涉實現線性操作

當具有相同頻率、相同振動方向和固定相位差的多束光疊加在一定空間時，會出現光強分布不同于多束光原始強度之和的現象，這就是干涉。

干涉和衍射在本質上是相同的，都是波的疊加，明暗的空間分布并不均勻；但二者在形成條件、分布規律和數學處理方法上存在差異。衍射是無數小元素振幅的疊加，通過積分計算得出。而干涉是有限數量光束的疊加，通過求和計算。可以說，衍射是一種復雜的干涉，事實上干涉和衍射往往是相輔相成的。干涉和衍射都可以實現線性求和。

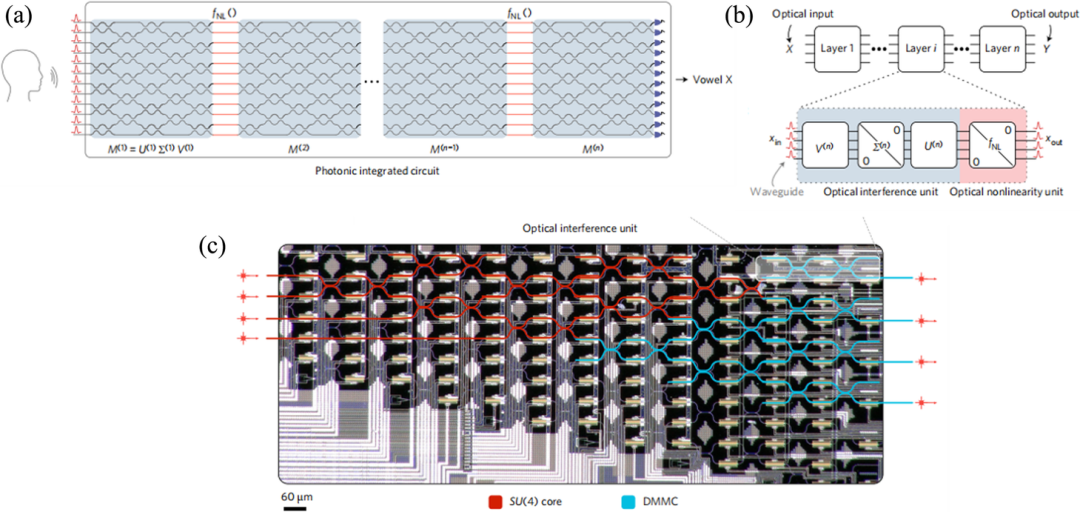
利用干涉原理實現神經網絡的線性運行。（a）相干納米光子電路。（b）神經網絡的每一層都由光干涉單元OIU和光非線性單元ONU組成

上圖顯示了一種新型全光神經網絡的光子芯片系統。光子芯片中光束的計算方法類似于干涉的基本原理，而線性運算則是由56個可編程馬赫-澤恩德干涉儀（MZI）組成的級聯陣列實現的。這種新方法使用多光束傳播，并利用波的相互作用產生干涉圖案，從而傳遞所需的操作結果。

原則上，采用這種結構的光學芯片可以運行傳統的人工智能算法，速度比傳統的電子芯片快得多，而能量卻不到后者的千分之一。

6）光的散射實現線性運行

當光線遇到障礙物或孔洞時，就會發生衍射；當多束光線相遇時，就會發生干涉；如果光線入射到不透明的表面或隨機介質上，就會被微小的顆粒從各方面反射回來，這就是所謂的散射，是科學家在20世紀60年代初首次發現的。

所謂散射，就是光強的空間分布、偏振態或頻率在傳播介質中分子或原子的作用下發生改變的現象。散射介質是引起散射現象的傳播介質。

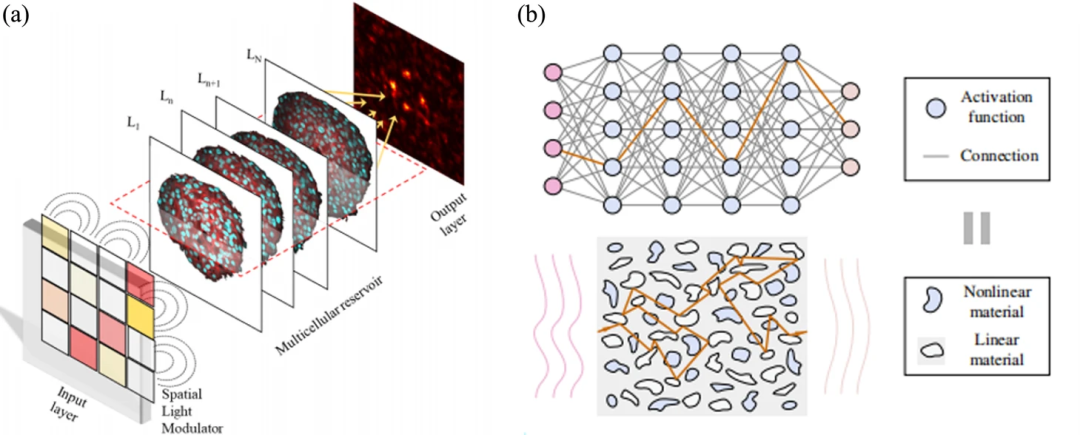
利用散射實現線性運行的光神經網絡。（a）由活性腫瘤細胞構建的深度ONN；（b）納米光子神經介質NNM

事實上，無論是衍射網絡的衍射調制層，還是腫瘤細胞的散射ONN，它們的網絡都是分層的。在以往的研究中，研究人員發現神經網絡需要適當的層數來完成特定的任務，這樣才能達到低損耗、高精度和良好的性能。如果網絡層數太少，其訓練推理能力達不到預期效果；如果層數太多，則容易出現梯度下降和過擬合問題，導致效果不佳，訓練時間極長。

當然，在光子神經網絡中，由于任務是以光速完成的，我們希望在保證實驗效果的前提下，層數越多越好，這樣才能訓練出更好的網絡，得到更準確的結果。因此，可以有這樣一個假設：存在一個無限層數的光神經網絡。

7）波分復用（WDM）實現線性運行

利用衍射原理實現光的線性工作，光信號在空氣中傳播。特定的傳輸介質（如散射介質）也可用于信號傳輸，或采用光纖，其傳輸帶寬寬、傳輸損耗低、抗干擾性強、重量輕、成本低，在光傳輸中具有明顯的優勢。

在光纖傳輸中，目前通常依靠波分復用技術。波分復用技術可以有效提高傳輸容量，實現光的分離與組成。因此，光纖可用于海量數據的計算。

2012年，帕戈（Yvan Paquot）等人成功構建了基于光纖系統的光電混合串行遞歸神經網絡，信號由任意波形發生器（AWG）注入，通過放大器和調制器對光進行調制。中間的存儲層由可變光衰減器、延遲線、反饋光電二極管、混頻器、放大器和馬赫-澤恩（Mach-Zehnder）調制器組成。該網絡可實現通信信道的均衡，是光子神經網絡在通信領域的場景拓展。

同年，F. Duport等人也利用光纖系統構建了全光循環神經網絡，采用光纖延遲切換單個非線性節點進行離線訓練。除了直接利用延遲線獲得延遲函數外，微環陣列和多模干擾分離器陣列等設備也能實現延遲。同時，采用多級或更復雜的時分復用，可大大提高信息處理速度，獲得更好的信息處理效果。

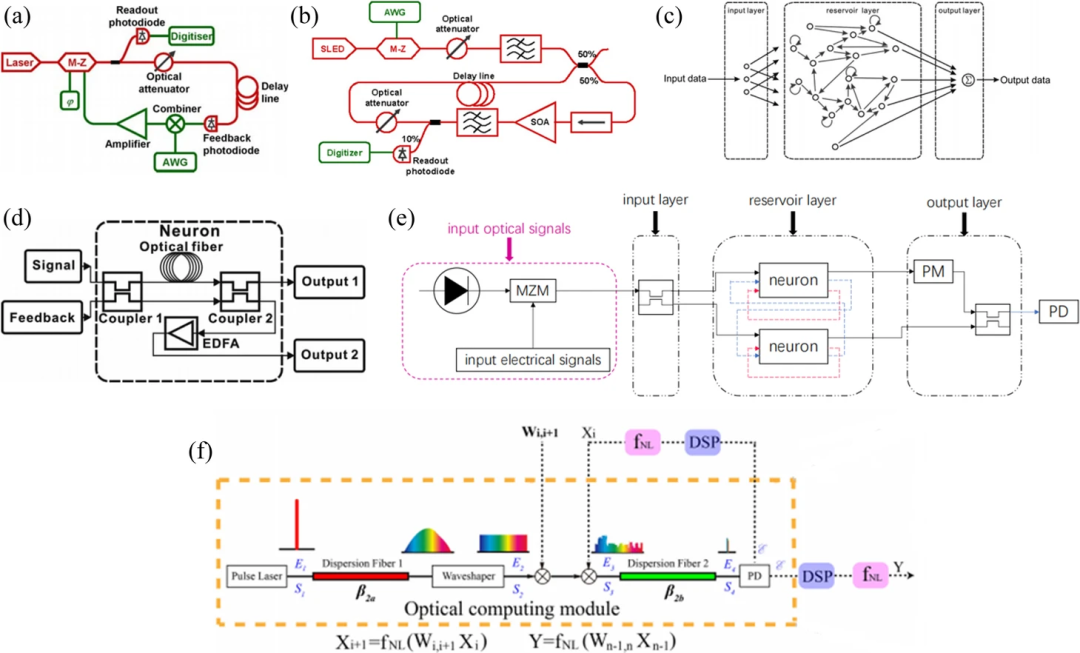
利用光纖實現的具有儲層計算功能的神經網絡。（a）光存儲計算。（b）全光存儲計算。（c, d, e）分別描述了儲層計算的原理，以及基于光纖通信系統構建的神經元和神經網絡的結構。（f）基于時域拉伸的串行電光神經網絡。

總之，無論是光波傳輸還是通信，光纖都是未來非常有潛力的發展方向。目前，光纖在波分復用技術、摻鉺光纖放大器EDFA等寬帶放大器技術、色散補償技術、孤子波分復用傳輸技術等方面都有非常成熟的表現。在光網絡方面，傳統的光網絡已經實現了節點間的全光化，但網絡節點上仍然使用電氣設備，這限制了其發展。

以光節點取代電節點的全光網絡將是未來光纖的重要發展方向。在5G時代，如何將光纖與光網絡相結合，實現真正的全光網絡，是一項可以深入研究的工程技術。

值得一提的是，在神經網絡中，波分復用技術的另一個典型應用是全光尖峰神經網絡，在這一領域也有一些科研進展，本文不詳細列舉。

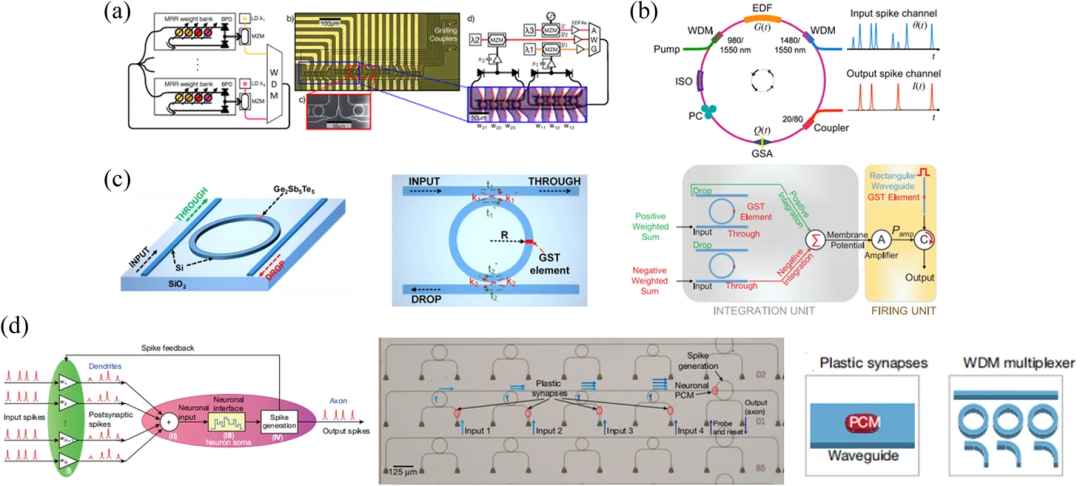
利用波分復用原理實現的光尖峰神經網絡。（a）第一個光子神經網絡的結構。（b）石墨烯尖峰神經元。（c）帶有GST的雙極積分發射神經元。（d）基于波分復用原理，由PCM和MRR陣列實現的全光尖峰神經突觸網絡結構。

神經網絡中僅有線性是不夠的，它還需要處理非線性激活函數，類似于大腦神經系統中突觸的功能。非線性函數可以加快網絡的收斂速度，提高識別準確率，是神經網絡不可或缺的一部分。沒有它，無論網絡層有多少，都可以歸結為龐大的線性運算，然而大多數問題都是非線性的。

激活函數的引入為神經元提供了非線性因子，使得神經網絡可以逼近任何非線性函數，從而使神經網絡可以應用于許多非線性模型。

在電子神經網絡中，我們可以使用現有的非線性激活函數，也可以定義一個函數來進行非線性運算。然而，在光子神經網絡中，這卻成為其發展的瓶頸；究其原因，非線性光學元件需要與大功率激光器相匹配，實現非線性功能的難度比電子器件更大，而且其實現的非線性功能具有很多非理想特性。

1967年，塞爾登（A. C. Selden）等人提出用飽和吸收體模型或電子模塊來實現光子神經網絡的非線性運算，但這種方法難以精確控制，需要通過光電二極管將光信號轉換為電信號，從而降低了運算速度。

目前，在光子神經網絡中實現非線性操作有兩種方法：一種是利用電子或光電方法，另一種是利用一些特殊材料的非線性效應。

1）非線性光學效應

非線性光學效應是介質在強光作用下的非線性偏振引起的效應，它源于分子和材料的非線性偏振，表現為光對介質的作用與介質響應之間的非線性關系。

在入射光場的作用下，構成介質的原子、分子或離子的運動狀態和電荷分布必須以一定的形式發生變化，從而形成電偶極子，產生電偶極矩，進而輻射出新的光波。在這個過程中，介質的電偏振強度矢量P是一個重要的物理量。P與入射光矢量E存在非線性關系：

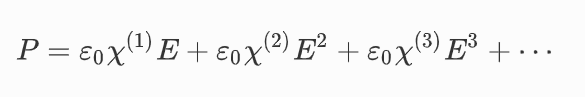
其中，χ(1) 、χ(2) 、χ(3)分別指介質的一階（線性）、二階和三階（非線性）極化率。并且，χ(1) 、χ(2) 和χ(3)依次減小。

非線性光學效應有很多種，按照電偏振強度和電場之間的關系可分為二階、三階和高階非線性光學效應。當然，我們一般只研究二階和三階非線性光學效應。根據激光與介質的相互作用方式，即兩者之間是否存在能量交換，可分為主動非線性光學效應和被動非線性光學效應；根據參數的變化，還可分為光頻率轉換效應、光非線性吸收、光克爾效應和自聚焦、光雙穩態效應、光相位共軛效應、受激散射效應等。

2）在光子神經網絡中實現非線性激活

在目前的光子神經網絡研究中，我們發現有些網絡中不存在光學非線性激活，或者是通過電子方式模擬的。例如，在衍射網絡D2NN中，就不存在激活函數。還有一些網絡利用非線性效應進行非線性激活設計。目前，飽和吸收、光學雙穩態和克爾效應已被視為ONN中潛在的激活函數。

光學吸收是指當光子進入介質時，原子和分子吸收光子的能量并發生能級轉換。在此過程中，如果光子的能量足夠強，介質的吸收系數就會隨著光強的變化而變化。這種變化可以是線性的，也可以是非線性的，即線性光吸收和非線性光吸收。非線性光學吸收的兩種主要光學機制是飽和吸收、反飽和吸收和雙光子吸收。

當激光入射到介質中時，介質的吸收系數會隨著介質中光強的增加而減小。當輸入光波的強度超過閾值時，介質的吸收特性開始變得飽和。這種非線性光學行為被稱為可飽和吸收。飽和吸收是由構成介質的粒子從基態水平過渡到第一激發態水平引起的。在飽和吸收的情況下，介質的吸收系數與介質中的光強I之間的關系可表示為：

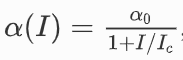
（a, b）飽和吸收的吸收系數和透射率曲線；（c）克爾型網絡結構

光非線性吸收可以通過光電器件和光學方法實現。光衰減放大器、摻鉺光纖放大器和半導體光放大器等光電器件的飽和可用作非線性激活。

在基于光纖通信系統的存儲計算中，每個神經元都由光纖和摻鉺光纖放大器兩個定向耦合器組成，而摻鉺光纖放大器實現了非線性功能，每個神經元都具有這樣的非線性激活功能。在光學方面，可飽和吸收體，如光學染料、石墨烯、C60等，都可以用來扮演非線性激活的角色。

當光束通過光學系統時，入射光強度和透射光強度之間存在非線性關系，從而實現光開關。例如，光學限制、光學雙穩態、各種干涉開關等。在電子學中，雙穩態是指在輸入相同電信號的情況下，具有兩個不同電阻值的單元電路。在光子學中，雙穩態是指光學元件在入射光強度相同的情況下，具有兩種不同水平的透射率，這就是光學雙穩態。它對于理解光學信息的存儲、運行和邏輯處理具有重要意義。

在非線性光學系統中，當輸入光強較小時，系統的輸出光強也較小。當輸入光強增加到某個臨界光強值時，系統的輸出光強就會跳到某個高光強狀態，就像打開了開關一樣。之后，如果輸入光強進一步降低，系統將不再回到原來臨界值的低光強狀態，而是會出現另一個較低光強的臨界值，使系統從高光強狀態躍遷到低光強狀態。在這個過程中，光學系統的輸入輸出傳遞關系中出現了“滯后”現象，類似于電磁學中的滯后環。

光雙穩態設備可用于高速光通信、光圖像處理、光存儲、光限幅器和光邏輯元件。特別是由半導體材料制成的光雙穩態器件，具有體積小、功耗低、開關時間短（10^-12 秒）等特點，未來很可能成為光計算機的邏輯元件。光學雙穩態因其巨大的潛在應用價值而成為一個非常活躍的研究領域。

克爾效應是三階非線性效應。在電場作用下，沿平行和垂直于電場方向的偏振光波的折射率n//和n⊥在介質中會發生不同的變化，它們之間的差值Δn與電場的二次方冪成正比，從而產生誘導雙折射。一般來說，外加電場是直流電場或低頻交變電場。如果光/光頻電場取代外加電場，當光線足夠強時，也會出現同樣的現象。此時，Δn與作用在介質中的激光束強度成正比，其中Δn為非線性相移，稱為光學克爾效應。如果需要優化的參數是相位，則可以利用光克爾效應實現非線性激活。

考慮到克爾非線性材料的快速響應和雙光子吸收的三階非線性光學效應，研究人員將克爾效應與雙光子吸收相結合，建立了一種非線性機制，并將其與InGaAsP環形諧振器結合使用，實現了全光存儲計算。

ONN是ENN的替代品，具有兩個明顯的優勢。

首先，ANN所依賴的矩陣乘法在ONN中可以以光速進行，檢測速率超過50GHz；其次，訓練后的ONN是無源的，可以用最小的功耗實現光信號的計算。

目前已有大量不同類型ONN的報道，包括基于衍射光學和自由空間光學的ONN、基于干涉光學和尖峰放電突觸機制的集成光子電路，甚至還有利用波分復用原理進行儲庫計算的神經網絡。

在衍射神經網絡的研究中，它很好地利用了光的衍射現象，實現了各層神經元之間的充分連接，從而使模型的學習能力更強。但他們的研究缺少一個重要部分，那就是非線性激活，研究人員還提出他們的研究過程不涉及非線性激活函數。未來，我們可以嘗試實現這種光學衍射神經網絡，并加入非線性工作，比如使用光折射晶體和磁光陷阱等非線性光學介質，或者使用現有的已經研究過的非線性激活函數，通過實驗來彌補它的缺失。

除此之外，這種網絡和基于傅立葉變換的ONN都屬于自由空間連接網絡。由于存在一些重型光學元件，如衍射元件和透鏡，因此對大量神經元進行縮放和擴展具有挑戰性。基于散射的神經網絡是一種值得研究的神經網絡。由于散射的無序性，光可能從各個方向散射。因此，光通過散射介質相當于多次計算，這很可能超越以往的分層前饋網絡。而且由于納米散射介質的特殊性，我們可以實現多種不同的實時訓練。

以芯片為主流的光學神經網絡，如相干納米光子電路和尖峰網絡，可以提供一種與CMOS兼容的、可擴展的方法來實現光學深度學習任務，在器件小型化和擴大網絡規模方面具有巨大優勢，而且它們可以在光照下工作，具有強大的計算能力和最小的資源消耗。但芯片式網絡成本極其昂貴，技術要求嚴格，需要大量人力物力支撐。因此，盡管它有著極好的發展前景，但仍有技術難題需要攻克。

非線性運算是神經網絡表達能力強的根本原因，它能使神經網絡學習輸入和輸出之間復雜的映射關系，加快網絡的收斂速度，提高識別精度。

它是神經網絡不可或缺的組成部分。目前已經出現了石墨烯、PCM、EIT等優秀的非線性激活劑，但在光域實現非線性功能還面臨著巨大的挑戰：首先，光非線性相對較弱，其產生一般需要很高的光功率，大大增加了能耗。同時，由于光功率過高，系統中的其他光學設備也會受到損壞。其次，光非線性需要與工作帶寬相平衡，ONN的信息處理能力將受到限制。此外，光路中的許多元件之間要保持一致的諧振響應，這就需要額外的控制電路來校準每個元件。

第三，在光子人工智能芯片的架構中，非線性激活函數的靈活性較高，光非線性效應難以控制。在非線性器件的制造過程中，響應趨于穩定，無法滿足靈活性的需求。同時，非線性光學單元的芯片集成在工藝兼容性和器件一致性方面也存在諸多問題。綜上所述，如何實現低功耗、高速度、易實現、表現形式豐富的光學非線性激活功能，是該領域技術人員亟待解決的技術難題。

除了在線性運算和非線性激活方面尋求突破，我們還可以把精力放在神經網絡的訓練上。目前，很多網絡都是在計算機上完成訓練過程，然后在光學系統中完成識別和分類任務，這樣的方法難免針對性太強。因此，尋找一種能在光學模式下訓練并實現實時訓練的訓練方法就顯得極為重要。相干納米光子電路實現了前向傳播可編程訓練，同時還提出了一種高效的局部訓練方法。納米散射介質的訓練也是一個很好的例子。它可以通過控制電場來改變材料的介電常數，從而控制內部摻雜劑的分布，最終達到穩定的效果。此外，根據任務或目標的不同，還可以多次重復訓練。

當然，ONN的成功實現離不開與其他領域技術的結合。例如，光柵衍射層的刻蝕需要半導體加工技術，芯片上搭載的相干納米光子電路、尖峰網絡和納米神經介質也需要硅光子集成技術。甚至與超材料、散射成像等領域也有合作。不僅如此，要實現非線性激活，還需要具備與化學和材料相關的知識儲備。

總之，作為光子技術和人工智能技術的交叉學科產物，光子神經網絡可以結合光子技術和人工智能的優勢，構建高速、低功耗、大帶寬的網絡結構，突破傳統電子神經網絡的瓶頸。然而，光子神經網絡仍需克服實時訓練、非線性激活函數的實現、規模和應用擴展等問題。相信在不久的將來，光子神經網絡能更好地發揮光電技術與人工智能技術結合帶來的優勢，從而更好地構建綠色智能世界。