一、場景
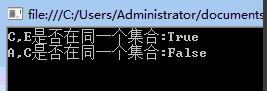
有時候我們會遇到這樣的場景,比如:M={1,4,6,8},N={2,4,5,7},我的需求就是判斷{1,2}是否屬于同一個集合,當然實現方法有很多,一般情況下,普通青年會做出 O(MN)的復雜度,那么有沒有更輕量級的復雜度呢?并查集就是用來解決這個問題的。
二、操作
從名字可以出來,并查集其實只有兩種操作,并(Union)和查(Find),并查集是一種算法,所以我們要給它選擇一個好的數據結構,通常我們用樹來作為它的底層實現。
2.1、節點定義
#region 樹節點/// <summary>/// 樹節點/// </summary>public class Node{/// <summary>/// 父節點/// </summary>public char parent;/// <summary>/// 節點的秩/// </summary>public int rank;}#endregion
2.2、Union 操作
<1> 原始方案
首先我們會對集合的所有元素進行打散,最后每個元素都是一個獨根的樹,然后我們 Union 其中某兩個元素,讓他們成為一個集合,最壞情況下我們進行 M 次的 Union 時會存在這樣的一個鏈表的場景。
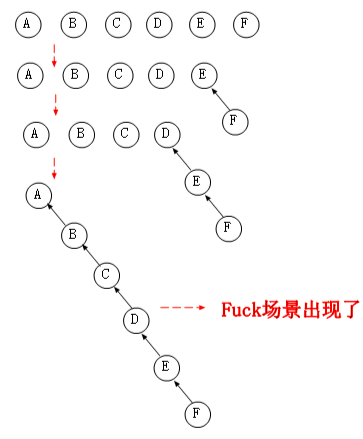
從圖中我們可以看到,Union 時出現了最壞的情況,而且這種情況還是比較容易出現的,最終導致在 Find 的時候就相當復雜了,為 O(N)。
<2> 按秩合并
我們發現出現這種情況的原因在于我們 Union 時都是將合并后的大樹作為小樹的孩子節點存在,那么我們在 Union 時能不能判斷一下,將小樹作為大樹的孩子節點存在,最終也就降低了新樹的深度,比如圖中的 Union(D,{E,F})的時候可以做出如下修改。
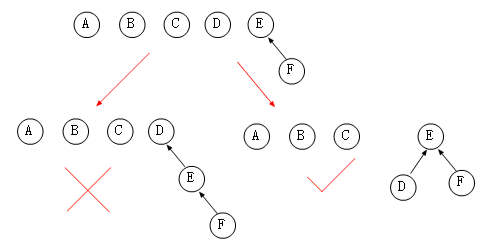
可以看出,我們有效的降低了樹的深度,在 N 個元素的集合中,構建樹的深度不會超過 LogN 層。M 次操作的復雜度為 O(MlogN),從代碼上來說,我們用 Rank 來統計樹的秩,可以理解為樹的高度,獨根樹時 Rank=0,當兩棵樹的 Rank 相同時,可以隨意挑選合并,在新根中的 Rank++ 就可以了。
#region 合并兩個不相交集合/// <summary>/// 合并兩個不相交集合/// </summary>/// <param name="root1"></param>/// <param name="root2"></param>/// <returns></returns>public void Union(char root1, char root2){char x1 = Find(root1);char y1 = Find(root2);//如果根節點相同則說明是同一個集合if (x1 == y1)return;//說明左集合的深度 < 右集合if (dic[x1].rank < dic[y1].rank){//將左集合指向右集合dic[x1].parent = y1;}else{//如果 秩 相等,則將 y1 并入到 x1 中,并將x1++if (dic[x1].rank == dic[y1].rank)dic[x1].rank++;dic[y1].parent = x1;}}#endregion
2.3、Find 操作
我們學算法,都希望能把一個問題優化到不能優化的地步,針對 logN 的級別,我們還能優化嗎?當然可以。
<1> 路徑壓縮
在 Union 和 Find 這兩種操作中,顯然我們在 Union 上面已經做到了極致,下面我們在 Find 上面考慮一下,是不是可以在 Find 上運用伸展樹的思想,這種伸展思想就是壓縮路徑。
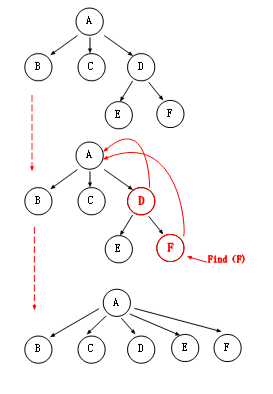
從圖中我們可以看出,當我 Find(F)的時候,找到“F”后,我們開始一直回溯,在回溯的過程中給,把該節點的父親指向根節點。最終我們會形成一個壓縮后的樹,當我們再次 Find(F)的時候,只要 O(1)的時間就可以獲取,這里有個注意的地方就是 Rank,當我們在路徑壓縮時,最后樹的高度可能會降低,可能你會意識到原先的 Rank 就需要修改了,所以我要說的就是,當路徑壓縮時,Rank 保存的就是樹高度的上界,而不僅僅是明確的樹高度,可以理解成"伸縮椅"伸時候的長度。
#region 查找x所屬的集合/// <summary>/// 查找x所屬的集合/// </summary>/// <param name="x"></param>/// <returns></returns>public char Find(char x){//如果相等,則說明已經到根節點了,返回根節點元素if (dic[x].parent == x)return x;//路徑壓縮(回溯的時候賦值,最終的值就是上面返回的"x",也就是一條路徑上全部被修改了)return dic[x].parent = Find(dic[x].parent);}#endregion
我們注意到,在路徑壓縮后,我們將 LogN 的復雜度降低到 Alpha(N),Alpha(N)可以理解成一個比 hash 函數還有小的常量,這就是算法的魅力。