1. 估計

貝葉斯框架下的數據收集，在以下條件下我們可以設計一個可選擇的分類器 :

P(wi) (先驗)；P(x | wi) (類條件密度)

但是。我們很少能夠完整的得到這些信息!

從一個傳統的樣本中設計一個分類器：

①先驗估計不成問題

②對類條件密度的估計存在兩個問題：1）樣本對于類條件估計太少了；2） 特征空間維數太大

了，計算復雜度太高。

如果可以將類條件密度參數化，則可以顯著降低難度。

例如：P(x | wi)的正態性，P(x | wi) ~ N( mi, Si)，用兩個參數表示，這樣就將概率密度估計問題轉

化為參數估計問題。

最大似然估計 (ML) 和貝葉斯估計；結果通常很接近, 但是方法本質是不同的。

最大似然估計將參數看作是確定的量，只是其值是未知!? 通過最大化所觀察的樣本概率得到最優的

參數—用分析方法。

貝葉斯方法把參數當成服從某種先驗概率分布的隨機變量，對樣本進行觀測的過程，就是把先驗概

率密度轉化成為后驗概率密度，使得對于每個新樣本，后驗概率密度函數在待估參數的真實值附近

形成最大尖峰。在參數估計完后，兩種方法都用后驗概率P(wi | x)表示分類準則!

2. 最大似然估計??

最大似然估計的優點：當樣本數目增加時，收斂性質會更好； 比其他可選擇的技術更加簡單。

2.1 基本原理

假設有c類樣本，并且每個樣本集的樣本都是獨立同分布的隨機變量；P(x | wj) 形式已知但參數未

知，例如P(x | wj) ~ N( mj, Sj)；記 P(x | wj) o P (x | wj, qj)，其中

使用訓練樣本提供的信息估計θ?= (θ1, θ2, …, θc), 每個 θi (i = 1, 2, …, c) 只和每一類相關 。

假定D包括n個樣本, x1, x2,…, xn，

θ的最大似然估計是通過定義最大化P(D | θ)的值，“θ值與實際觀察中的訓練樣本最相符”

最優估計：令并令為梯度算子，the gradient operator

我們定義 l(θ) 為對數似然函數：l(θ) = ln P(D | θ)

新問題陳述：求解 θ?為使對數似然最大的值? ??

對數似然函數l(θθ)顯然是依賴于樣本集D, 有：

最優求解條件如下：

令，來求解。

2.2 高斯情況：μ未知

P(xk | μ) ~ N(μ???????, Σ)：(樣本從一組多變量正態分布中提取)

θ?= μ，因此：μ的最大似然估計必須滿足?

乘Σ并且重新排序, 我們得到：即訓練樣本的算術平均值!

結論：如果P(xk | wj) (j = 1, 2, …, c)被假定為d?維特征空間中的高斯分布；然后我們能夠估計向量

?從而得到最優分類!

2.3?高斯情況：μ???????和Σ未知

未知 μ????????和 σ，對于單樣本xk：θ?= (θ1, θ2) = (μ, σ2)

對于全部樣本，最后得到：

聯合公式 (1) 和 (2), 得到如下結果：

3. 貝葉斯估計?

在最大似然估計中 θ?被假定為固定值；在貝葉斯估計中 θ?是隨機變量

3.1?類條件密度

目標: 計算 P(wi | x, D)，假設樣本為D，貝葉斯方程可以寫成：

先驗概率通常可以事先獲得，因此

每個樣本只依賴于所屬的類，有：

即：只要在每類中，獨立計算就可以確定x的類別。

因此，核心工作就是要估計

3.2 參數分布

假設??的形式已知, 參數θ的值未知，因此條件概率密度?的函數形式是知道的；假設參

數q是隨機變量，先驗概率密度函數p(θ)已知，利用貝葉斯公式可以計算后驗概率密度函數p(θ|D)；

希望后驗概率密度函數p(θ?| D) 在θ的真實值附件有非常顯著的尖峰，則可以使用后驗密度p(θ?| D)

估計 θ?；注意到：

如果p(θ|D) 在某個值附件有非常顯著的尖峰，即如果條件概率密度具有一個已知的形式，則利

用已有的訓練樣本，就能夠通過p(θ?| D) 對p(x?| D) 進行估計。

?3.3 高斯過程

單變量情形的 p(μ?| D)

復制密度：

其中：?

結論：

單變量情形的 p(x|D)：

?多變量情形：

復制密度：?

其中：

利用：，

得：。

利用：，令y=x-μ???????。

4. 貝葉斯參數估計一般理論?

p(x | D) 的計算可推廣于所有能參數化未知密度的情況中，基本假設如下:

假定 p(x |?θ) 的形式未知，但是q的值未知。q被假定為滿足一個已知的先驗密度 P(θ)。

其余的 θ?的信息包含在集合D中，其中D是由n維隨機變量x1, x2, …, xn組成的集合，它們服從于概

率密度函數p(x)。

基本的問題是：計算先驗密度p(θ?| D) ，然后 推導出 p(x | D)。

遞歸貝葉斯學習：

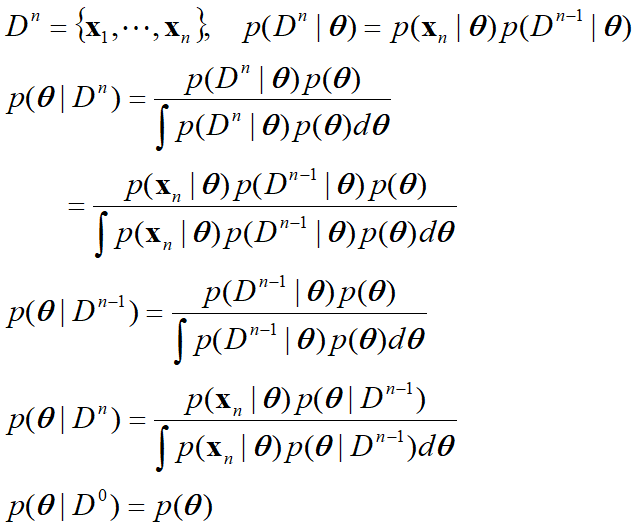
該過程稱為參數估計的遞歸貝葉斯方法，一種增量學習方法。

唯一性問題：

p(x|θ) 是唯一的：后驗概率序列 p(θ|Dn) 收斂到 delta 函數；只要訓練樣本足夠多，則 p(x|θ) 能唯

一確定θ。

在某些情況下，不同θ值會產生同一個 p(x|θ) 。p(θ|Dn) 將在 θ?附近產生峰值，這時不管p(x|θ) 是

否唯一， p(x|Dn)總會收斂到p(x) 。因此不確定性客觀存在。

最大似然估計和貝葉斯參數估計的區別：

	最大似然估計	貝葉斯參數估計
計算復雜度	微分	多重積分
可理解性	確定易理解	不確定不易理解
先驗信息的信任程度	不準確	準確
例如 p(x|q)	與初始假設一致	與初始假設不一致

?

?

?

?

?

?

?