1.分類模型評價指標
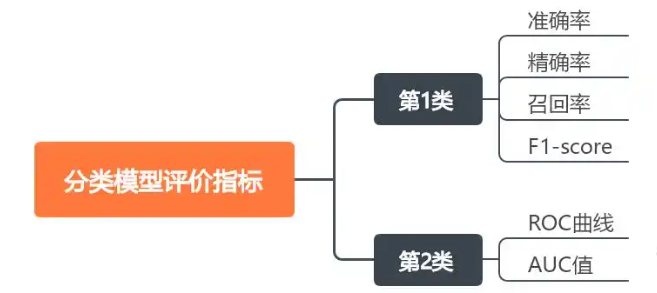
在模型評估中,有多個標準用于衡量模型的性能,這些標準包括準確率(Accuracy)、精確率(Precision)、召回率(Recall)、F1 分數(F1-Score)等。
P positive;N? Negative
真正例(TP) :模型正確預測為正類的樣本數量。
它真實標簽是什么,預測值就是什么這就是TP
真負例(TN) :模型正確預測為負類的樣本數量。
真實標簽和預測標簽不一樣
假正例(FP) :模型錯誤預測為正類的樣本數量。
比如預測標簽是0,真實標簽不是0,那么就是一個FP0
假負例(FN) :模型錯誤預測為負類的樣本數量。
FN = 該類別真實樣本數 - 正確預測數(TP)
比如真實標簽0有3個? 預測里面正確預測到了倆個 那么FN = 1
1. 理解數據
真實標簽:
y_true = [2, 0, 2, 2, 0, 1]預測標簽:
y_pred = [0, 0, 2, 2, 0, 2]2. 構建混淆矩陣
首先計算混淆矩陣(按類別0、1、2排列):
真實\預測 0 1 2 0 2 0 0 1 0 0 1 2 1 0 2
類別0:真實為0的樣本(索引1和4)
預測結果:兩個都被正確預測為0 →?TP=2
其他類別預測為0的樣本:真實為2的樣本(索引0)被預測為0 →?FP=1
Precision? = TP / (TP + FP) = 2 / (2 + 1) =?2/3
類別1:真實為1的樣本(索引5)
預測結果:真實為1被預測為2 →?TP=0
其他類別預測為1的樣本:無 →?FP=0
Precision? = 0 / (0 + 0) =?0(sklearn將分母為0時定義為0)
類別2:真實為2的樣本(索引0、2、3)
預測結果:索引2和3正確預測為2 →?TP=2
其他類別預測為2的樣本:真實為1(索引5)被預測為2 →?FP=1
Precision? = 2 / (2 + 1) =?2/3
計算每個類別的FN
FN是行方向的誤差(真實類別被漏判的數量)。對每個類別:
text
FN = 該類別真實樣本數 - 正確預測數(TP)1.?類別 0
真實樣本數:2個(索引1和4)
正確預測數(TP):2個(都被預測為0)
FN? = 2 - 2 = 0
2.?類別 1
真實樣本數:1個(索引5)
正確預測數(TP):0個(未被預測為1)
FN? = 1 - 0 = 1
(真實為1的樣本被錯誤預測為2)3.?類別 2
真實樣本數:3個(索引0、2、3)
正確預測數(TP):2個(索引2和3被正確預測為2)
FN? = 3 - 2 = 1
(真實為2的樣本被錯誤預測為0)
2.準確率
準確率(Accuracy)準確率是最直觀的評估指標,它表示模型預測正確的樣本占總樣本的比例。計算公式為:
![]()
from sklearn.metrics import confusion_matrix,accuracy_score
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns# 假設我們有以下真實標簽和預測結果
y_true = np.array([2, 0, 2, 2, 0, 1])
y_pred = np.array([0, 0, 2, 2, 0, 2])# 計算準確率
accuracy = accuracy_score(y_true, y_pred)
print("準確率:", accuracy)?
?
3.精確率(Precision)
精確率衡量模型預測為正類的實例中,實際為正類的比例。計算公式為:
![]()
?
對應多分類問題,采樣宏平均精確率是每個類別的精確率的平均值,不考慮每個類別的樣本數量。計算公式如下:
![]()
?
?
from sklearn.metrics import confusion_matrix,accuracy_score,precision_score
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns# 假設我們有以下真實標簽和預測結果
y_true = np.array([2, 0, 2, 2, 0, 1])
y_pred = np.array([0, 0, 2, 2, 0, 2])# 計算精確率
precision = precision_score(y_true, y_pred, average='macro')
print("精確率:", precision)4.召回率(Recall)
召回率衡量所有實際為正類的樣本中,模型預測為正類的比例。計算公式為:
![]()
召回率關注的是模型捕捉正類樣本的能力。在某些領域,如醫療診斷,召回率尤其重要,因為漏診(假負例)的后果可能非常嚴重。
?
from sklearn.metrics import confusion_matrix,accuracy_score,precision_score,recall_score
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns# 假設我們有以下真實標簽和預測結果
y_true = np.array([2, 0, 2, 2, 0, 1])
y_pred = np.array([0, 0, 2, 2, 0, 2])# 計算召回率
recall = recall_score(y_true, y_pred, average='macro')
print("召回率:", recall)?
5.F1 分數(F1-Score)
F1分數是精確率和召回率的調和平均值,它平衡了這兩個指標。計算公式為:
![]()
F1分數在精確率和召回率都較高的算法上表現出色。它是一個綜合指標,特別適用于那些對精確率和召回率都同樣重視的場景。
from sklearn.metrics import confusion_matrix,accuracy_score,precision_score,recall_score,f1_score
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns# 假設我們有以下真實標簽和預測結果
y_true = np.array([2, 0, 2, 2, 0, 1])
y_pred = np.array([0, 0, 2, 2, 0, 2])# 計算準確率
accuracy = accuracy_score(y_true, y_pred)
print("準確率:", accuracy)# 計算精確率
precision = precision_score(y_true, y_pred, average='macro')
print("精確率:", precision)# 計算召回率
recall = recall_score(y_true, y_pred, average='macro')
print("召回率:", recall)# 計算F1分數
f1 = f1_score(y_true, y_pred, average='macro')
print("F1分數:", f1)6.混淆矩陣
混淆矩陣是評估分類問題的基礎工具,它是一個表格,顯示了分類算法的預測結果與真實標簽之間的關系。對于二分類問題,混淆矩陣包含真正例(TP)、真負例(TN)、假正例(FP)和假負例(FN)。這些值是計算其他評估指標的基礎。混淆矩陣不僅提供了一個直觀的視覺表示,還允許我們深入了解模型在各個類別上的表現,特別是當處理不平衡數據集時,混淆矩陣可以揭示模型是否傾向于錯誤地將一個類別分類為另一個類別。
from sklearn.metrics import confusion_matrix,accuracy_score,precision_score,recall_score,f1_score
import numpy as np
import matplotlib.pyplot as plt
import seaborn as snsy_true = np.array([2, 0, 2, 2, 0, 1])
y_pred = np.array([0, 0, 2, 2, 0, 2])cm = confusion_matrix(y_true, y_pred)
plt.figure(figsize=(10,7))
sns.heatmap(cm, annot=True,fmt = "d",cmap = "Blues")
plt.xlabel('Predicted')
plt.ylabel('Truth')
plt.show()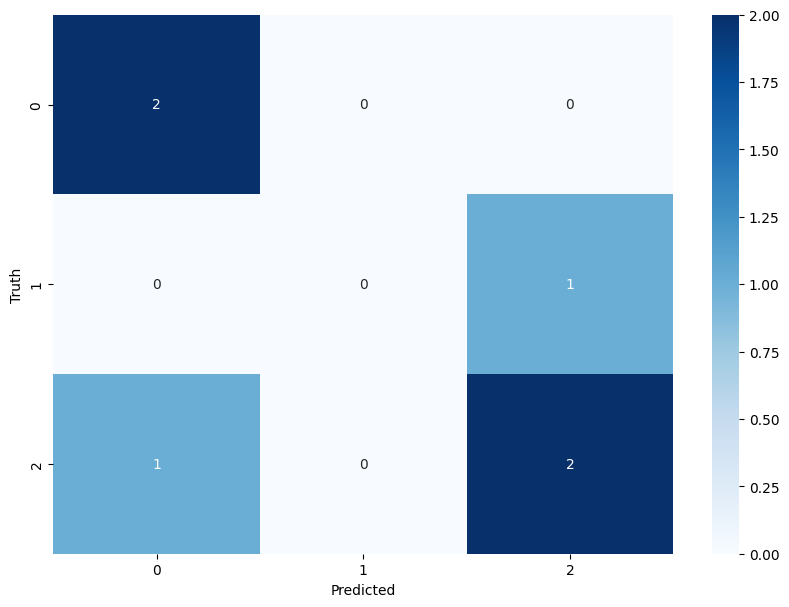
?
7.ROC曲線和AUC值
ROC曲線是一個性能度量,顯示了在不同閾值設置下模型的真正例率(召回率)和假正例率的關系。AUC值表示ROC曲線下的面積,用于衡量模型的整體性能,AUC值越高,模型性能越好。ROC曲線和AUC值是評估模型區分不同類別能力的重要工具,尤其在二分類問題中非常實用。
from sklearn.metrics import roc_curve,roc_auc_score
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
import numpy as np
import matplotlib.pyplot as pltX = np.array([[0,0],[1,1],[2,0],[2,2],[0,1]])
y = np.array([1,1,0,1,0])plt.scatter(X[y==0,0],X[y==0,1],color = "red",label = "Class 0")
plt.scatter(X[y==1,0],X[y==1,1],color = "blue",label = "Class 1")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.legend()
plt.title("Data Points by Class")
plt.grid(True)
plt.show()x_train,x_test,y_train,y_test = train_test_split(X,y,test_size = 0.4,random_state = 42)
print("------訓練樣本------")
print(x_train,y_train)
print("------測試樣本------")
print(x_test,y_test)clf = RandomForestClassifier(n_estimators = 100,max_depth = 2,random_state = 42)
clf.fit(x_train,y_train)y_scores = clf.predict_proba(x_test)[:,1]
fpr,tpr,thresholds = roc_curve(y_test,y_scores)
auc = roc_auc_score(y_test,y_scores)plt.figure()
plt.plot(fpr,tpr,color = "darkorange",lw = 2,label = "ROC curve (area = %0.2f)" % auc)
plt.plot([0,1],[0,1],color = "navy",lw = 2,linestyle = "--")
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()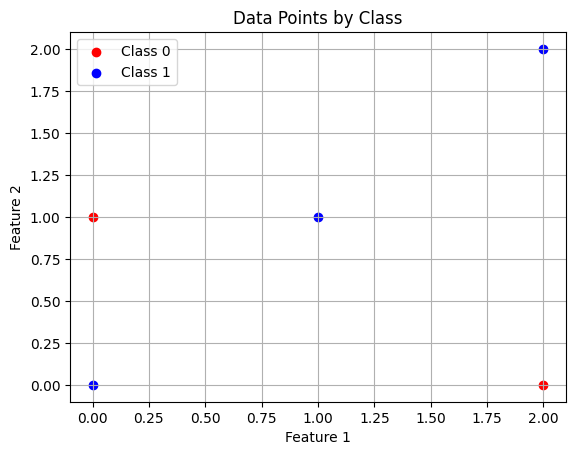 | 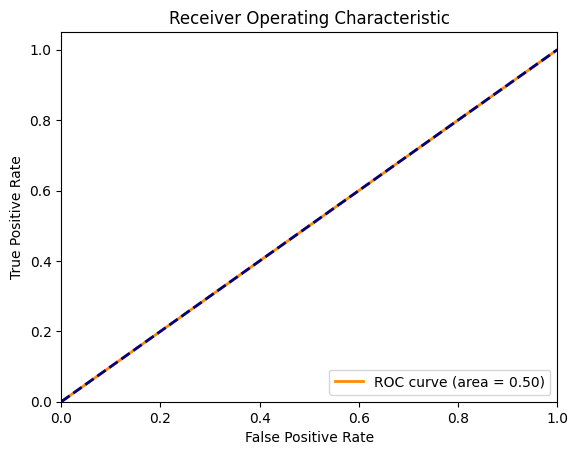 |









![[論文閱讀] 人工智能 + 軟件工程 | NoCode-bench:評估LLM無代碼功能添加能力的新基準](http://pic.xiahunao.cn/[論文閱讀] 人工智能 + 軟件工程 | NoCode-bench:評估LLM無代碼功能添加能力的新基準)









