每日一題系列(day 01)
前言:
🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈
?? 🔎🔎如果說代碼有靈魂,那么它的靈魂一定是👉👉算法👈👈,因此,想要寫出💚優美的程序💚,核心算法是必不可少的,少年,你渴望力量嗎😆😆,想掌握程序的靈魂嗎???那么就必須踏上這樣一條漫長的道路🏇🏇,我們要做的,就是斬妖除魔💥💥,打怪升級!💪💪當然切記不可😈走火入魔😈,每日打怪,日日累積,終能成圣🙏🙏!今天就開啟我們的斬妖之旅!????
LeetCode-589.N叉樹的前序遍歷:
題目:
給定一個 n 叉樹的根節點 root ,返回 其節點值的 前序遍歷 。n 叉樹 在輸入中按層序遍歷進行序列化表示,每組子節點由空值 null 分隔(請參見示例)。
示例1:
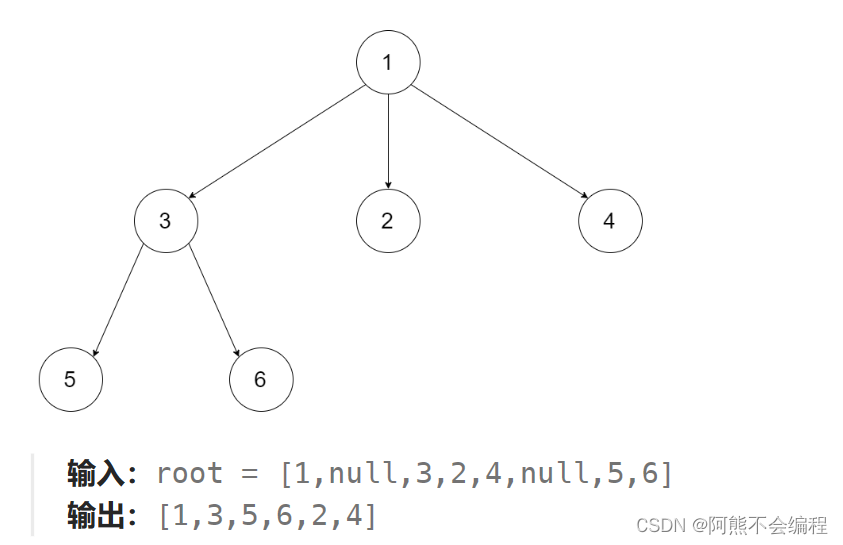
示例2:
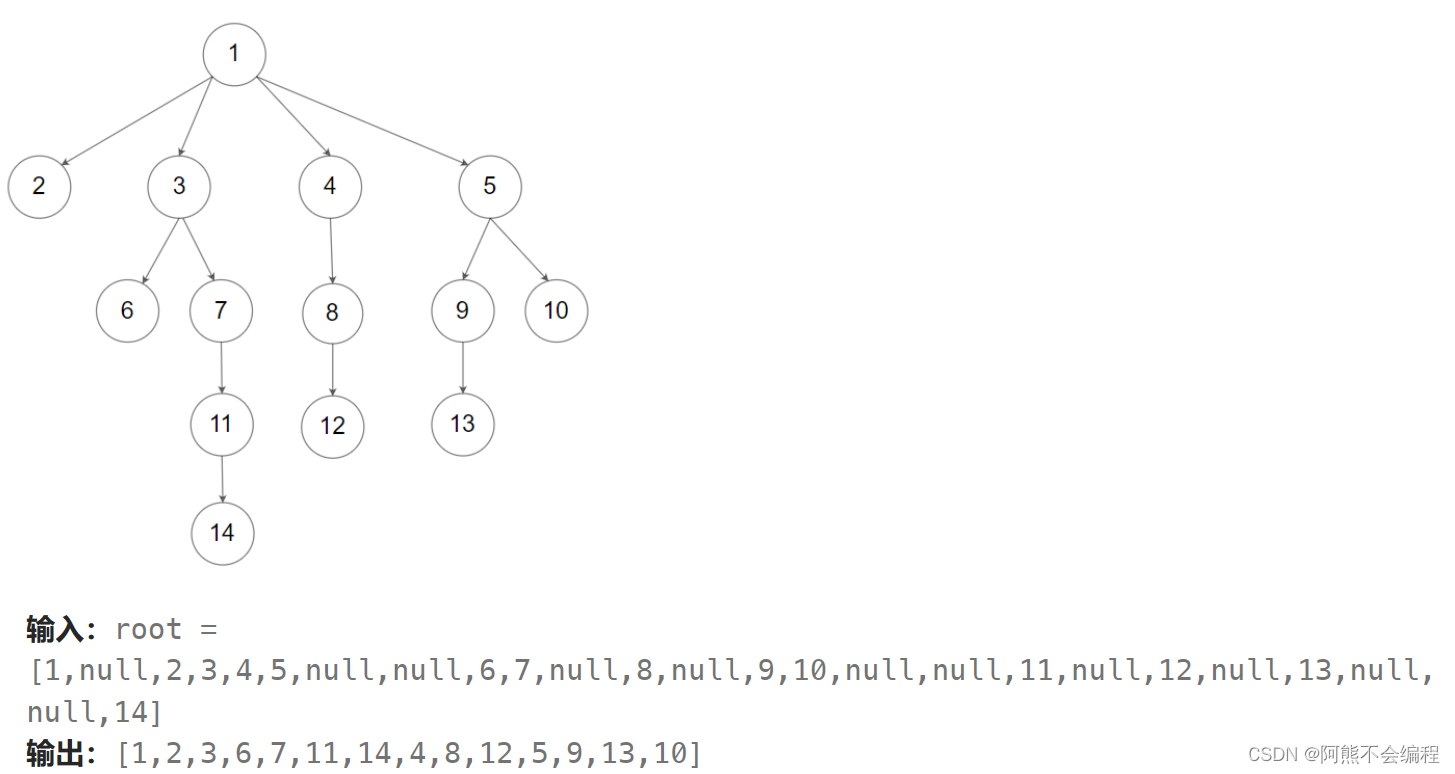
注意事項:
- 節點總數在范圍 [0, 104]內
- 0 <= Node.val <= 104
- n 叉樹的高度小于或等于 1000
解法一:
??思路:
??首先開辟一個數組,用來存放N叉樹前序遍歷的結果,先將根節點壓入數組,然后進行范圍for(順序遍歷二叉樹的每一個節點),將前序遍歷的結果放入到tmp數組中,再使用范圍for將tmp數組的值拷貝回原數組。最后返回原數組的值即可。
??但是這樣寫的效率非常低,將ans數組拷貝到tmp數組,再將tmp數組拷貝回原數組,這樣來來回回的拷貝效率實在是很低,所以我們可以考慮用封裝來優化。
??代碼實現:
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:vector<int> preorder(Node* root) {if(root == NULL) return vector<int>{};vector<int> ans;//開辟一個數組用來記錄前序遍歷結果ans.push_back(root -> val);//將前序遍歷到的每個節點的值壓入到數組中for(auto x : root -> children)//范圍for依次遍歷N叉樹的每個節點{vector<int> tmp = preorder(x);//用tmp數組接收前序遍歷的結果for(auto y : tmp) ans.push_back(y);//拷貝完成之后再將tmp數組元素拷貝回原數組}return ans;//返回前序遍歷數組的結果即可}
};
解法二:
??思路:
??以上是不使用封裝解決前序遍歷問題的方法,沒有什么問題是一層封裝解決不了的,如果有,那就兩層。
??1、我們在preorder函數中定義一個數組ans用來記錄前序遍歷結果,封裝一個前序遍歷的函數,將根節點和數組傳ans入函數,其中數組傳參是用引用傳參(避免多一次拷貝)最后返回數組即可。
??2、在函數內部,我們首先將遍歷到的每個節點的值壓入到數組ans當中,再使用范圍for對N叉樹的每個子孩子遍歷,并且將前序遍歷到的節點全部拷貝到ans數組中。
時間復雜度:O(N),其中 n 為 N 叉樹的節點。每個節點恰好被遍歷一次。
空間復雜度:O(N),遞歸過程中需要調用棧的開銷,平均情況下為 O(log?N),最壞情況下樹的深度為 N?1,此時需要的空間復雜度為 O(N)。
??代碼實現:
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:void _preorder(Node *root, vector<int> &ans)//引用傳參,少一次拷貝構造{if(root == NULL) return;ans.push_back(root -> val);//將前序遍歷的節點值壓入數組中for(auto x : root -> children)//范圍for便利{_preorder(x, ans);//將前序遍歷結果也壓入到ans數組中}return;}vector<int> preorder(Node* root) {vector<int> ans;//記錄前序遍歷的結果_preorder(root, ans);//進行前序遍歷return ans;//返回前序遍歷的數組}
};
??今天第一次寫的題也是比較簡單的,主要是對數組拷貝的優化,將多次拷貝優化為在一個數組內操作。



)



: Index is supposed to be a vector)









)

