【追求卓越09】算法--散列表（哈希表）

引導

????????通過前面幾個章節的學習（二分查找，跳表），我們發現想要快速查找某一個元素，首先需要將所有元素進行排序，再利用二分法思想進行查找，復雜度是O(logn)。有沒有更快的查找方式呢？

????????本章介紹一下我們工作中經常接觸到的散列表（哈希表）。它能夠使查找的效率達到O(1)。主要是理論方面，讓大家開始了解哈希思想。

散列表

????????提到查找復雜度是O(1)，我們在前面接觸到的就是數組了。散列思想就是基于數組支持下標隨機訪問數據特想實現的。那么問題就是如何將元素和數組下標進行映射？

????????例：學校開運動會，有100個運動員，編號是0~99。我要查找86號運動員的信息，該怎么做呢？

????????思路：我們可以建立一個數組，將標號和數組下標一一對應，訪問哪一個標號的運動員，直接查找對應數組下標即可。

????????該散列思想中，編號我們稱作為鍵或者關鍵字。將關鍵字轉換為數組下標的，我們稱作為散列函數。而散列函數計算得到的值就叫做散列值（數組下標）。

????????散列思想：散列表用的就是數組支持按照下標隨機訪問。當我們通過散列函數將元素的鍵值映射為數組下標時，然后將數組保存到數組對應位置中。當我們查找都一個元素時，我們使用同一個散列函數，將鍵值轉化為數組下標，從對應的數組下標獲取數據。

散列函數

????????從散列思想中，我們可以知道散列表中散列函數起到很重要的作用。針對不同的問題，散列函數都可能不同。比如上面的例子，我可以設置這樣的哈希函數：

int hash(int key)
{
??? return key;
}
/*將關鍵字作為下標*/

由于該例子較為簡單，也比較容易想到。但是無論什么想的問題，我覺得散列函數應該盡量做到一下幾點：

散列函數計算得到的散列值是一個非負整數。因為散列值會作為數組下標。
如果key1 == key2,那么hash(key1)==hash(key2)。
如果key1 != key2,那么hash(key1)!=hash(key2)。

其中1，2好理解，但是3實際上是很實現的。因為數組的大小是有限的，但是不同元素可能會有很多。這就導致肯定會存在key1 != key2,hash(key1)==hash(key2)的情況。這種情況我們稱之為散列沖突。再優秀的散列函數也避免不了散列沖突。

散列沖突的解決方式

散列沖突的解決方式有兩種：開放尋址法，鏈表法。

開放尋址法

開放尋址法的思想是：出現了散列沖突，我們就重新探測到一個空閑位置，將其插入。

如何探測空閑位置？

????????如果某個數據經過散列函數之后，存儲位置已經被占用了，我們就從當前位子開始，依次往后查找，看是否有空閑位子，直到找到為止。

如何查找？

????????通過散列函數求出要查找出的鍵值對應的散列值，然后比較數組中下標為散列值的元素和要查找的元素。如果相等，則說明是我們要找的元素；否則繼續往后查找。如果遍歷到空閑位子，還沒有找到，則說明散列表中沒有要查找的元素。

刪除的注意事項？

????????我們知道散列表有查找操作肯定也有刪除操作。當我們刪除一個元素時，如果將其設置為空閑，那么在查找的過程中就會出現問題（原本在散列表中的元素，會認定為不存在）。我們可以將刪除的元素置為delete狀態。該狀態的位子，可以插入數據。查找的時候，不必停下來，繼續向后查找。

開放尋址法的缺點?

????????從開放尋址法的思想中，我們可以考慮到，當散列表中的元素越來越多的時候，散列沖突可能性越來越大，空閑位置越來越少，線性探測的時間就會越來越久。極端情況下，我們可能需要探測整個散列表，最壞的情況下，時間復雜度是O(n)。

裝載因子

一般情況下，我們會盡量保證散列表中有一定比例的空閑槽位，我們用裝載因子表示空位的多少。

散列表的裝載因子=填入表中的元素個數/散列表的長度

鏈表法

????????鏈表法相對于開發尋址法較為簡單，也容易理解。使用的是指針數組結構。數組元素對應的是一個鏈表，所有散列值相同的元素都在一個鏈表中。如圖：

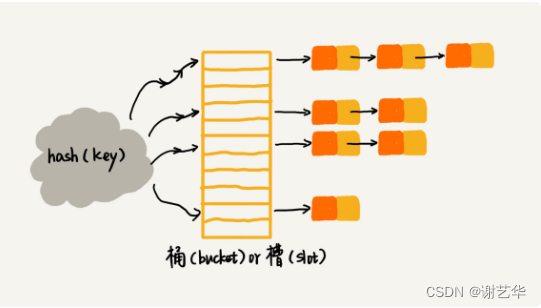
????????那么鏈表法的插入操作，我們選擇鏈表的頭插，所以時間復雜度是O(1)。

????????但是查找和刪除操作的時間復雜度是O(k),k表示鏈表的長度。理論上每個鏈表的長度應該是均勻的，k=n/m。m是散列表的長度。這就要求散列表的優秀。若散列表不夠好，那么查找和刪除的復雜度可能會退化到O(n)。

如何設計散列函數

????????我們知道散列函數是散列表中重要的一個部分，它的好壞，決定了散列沖突的概率以及散列表的性能。

????????散列函數在設計的時候除了盡量遵循，上章節中指明的三點，還要考慮下面幾點因素：

散列函數不能設計的太復雜。復雜的散列函數會消耗過多的資源，間接影響性能。
散列值盡量隨機并且分布均勻。這樣才能降低散列沖突的概率，即使出現散列沖突，每個鏈表長度也比較均勻（針對鏈表法）

????????常見的散列函數的設計方法：數據分析法，直接尋址法，平方取中法，折疊法，隨機數法等。

裝載因子調整

????????我們知道當裝載因子過大的時候，說明散列表中的元素越多，空閑位置越少，散列沖突的概率就會越大。

????????對于沒有頻繁插入和刪除的靜態散列表，我們可以設計出一個完美的散列表。因為數據都是我們提前已知的。

????????但是對于動態的散列表，數據集合是動態變化的。我們無法事先申請一個足夠大的散列表。但是當裝載因子逐漸變大，散列沖突變得無法接受的時候，我們就需要動態擴容。

????????比如當散列表的裝載因子是0.8時，我們將散列表擴容一倍，那么裝載因子就變為了0.4。僅僅將散列表擴容就可以嗎？

????????散列表擴容之后，我們需要將原先的散列表拷貝到新的散列表中。這個過程需要重新進行散列函數計算。

問題：我們知道在擴容的時候，涉及到數據的搬移，這會消耗很多時間。這就導致響應不及時。該如何處理？

解：這種動態擴容，直接將數據進行搬移的方式，非常的耗時，用戶體驗很不好（出現概率較低）。我們可以進行優化，將數據搬移的操作進行分批處理。第一次進行擴容，我們只申請散列表，并將數據插入，不進行數據的搬移。當下次再插入數據時，我們從舊的散列表中拷貝一個到新的散列表（舊的delete）。一直當舊的散列表全部被搬移完。在這個過程中，我們查詢時，需要先舊的散列表中查詢，查詢不到，再到新的散列表中查詢。如果都沒有，說明不存在。這種均攤的方式，將任何情況下，插入操作的時間復雜度是O(1);