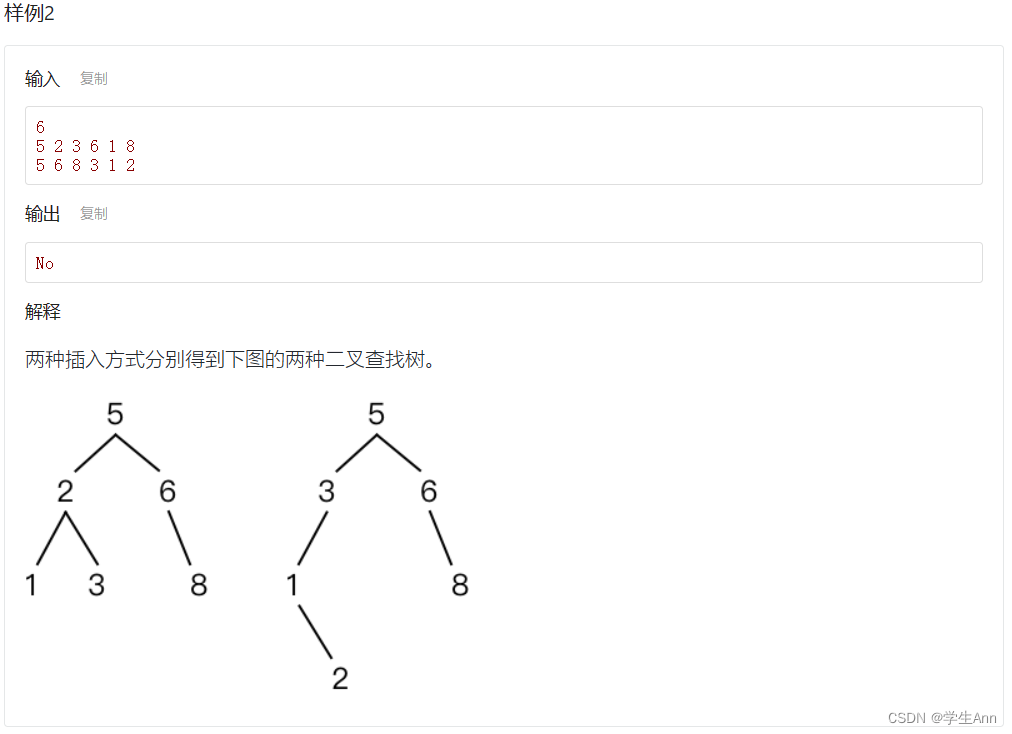
將第一組n?個互不相同的正整數先后插入到一棵空的二叉查找樹中，得到二叉查找樹T1?；再將第二組n個互不相同的正整數先后插入到一棵空的二叉查找樹中，得到二叉查找樹T2?。判斷T1?和T2??是否是同一棵二叉查找樹。

二叉查找(搜索)樹定義：

?①要么二叉查找樹是一顆空樹。

②要么二叉查找樹由根節點、左子樹、右子樹構成，其中左子樹和右子樹都是二叉查找樹，且左子樹上所有結點的數據域都小于或等于根結點的數據域，右子樹上所有的結點的數據域均大于根節點的數據域。

由定義可以發現這么一個二叉查找樹的性質：

二叉查找樹如果中序遍歷（左兒子，根結點，右兒子）得到的必定是一個由小到大的有序序列。

而正是因為這么一個性質，才被稱為查找樹。

回到本題解題思路：

根據給定的兩組數進行建立二叉查找樹，然后進行先序遍歷得到序列，若二者的先序遍歷序列相等，則說明為同一棵樹。

完整代碼如下：

#include <iostream>
#include <vector>
using namespace std;struct node{int data;int lchild;int rchild;
}nodes[51];int nodecount = 0;
vector<int> tree1,tree2;void PreOrderTraverse(int root,vector<int>& tree){//注意要用引用，這樣才改變內容，不然只是淺拷貝。if(root == -1){return;}tree.push_back(nodes[root].data);PreOrderTraverse(nodes[root].lchild,tree);PreOrderTraverse(nodes[root].rchild,tree);
}int newNode(int data){nodes[nodecount].data = data;nodes[nodecount].lchild = -1;nodes[nodecount].rchild = -1;return nodecount++;
}int insert(int root,int data){if(root == -1){//若根結點為-1，則說明找到了插入的位置。return newNode(data);}if(data<nodes[root].data){//利用二叉查找樹的性質nodes[root].lchild = insert(nodes[root].lchild,data);}else{nodes[root].rchild = insert(nodes[root].rchild,data);}return root;
}int buildtree(int n,int data[]){nodecount = 0;int root = -1;//一開始樹為空。for(int i=0;i<n;i++){root = insert(root,data[i]);}return root;
}int main(){int n;cin>>n;int data[n];for(int i=0;i<n;i++){cin>>data[i];}int root = buildtree(n,data);PreOrderTraverse(root,tree1);for(int i=0;i<n;i++){cin>>data[i];}root = buildtree(n,data);PreOrderTraverse(root,tree2);if(tree1==tree2){cout<<"Yes"<<endl;}else{cout<<"No"<<endl;}return 0;
}