題意：略，題中較清晰。

用二叉查找樹來存儲數據，為了增加效率，盡量使左子樹和右子樹的深度差不超過一，這樣可以時間控制在logn，效率比較高。

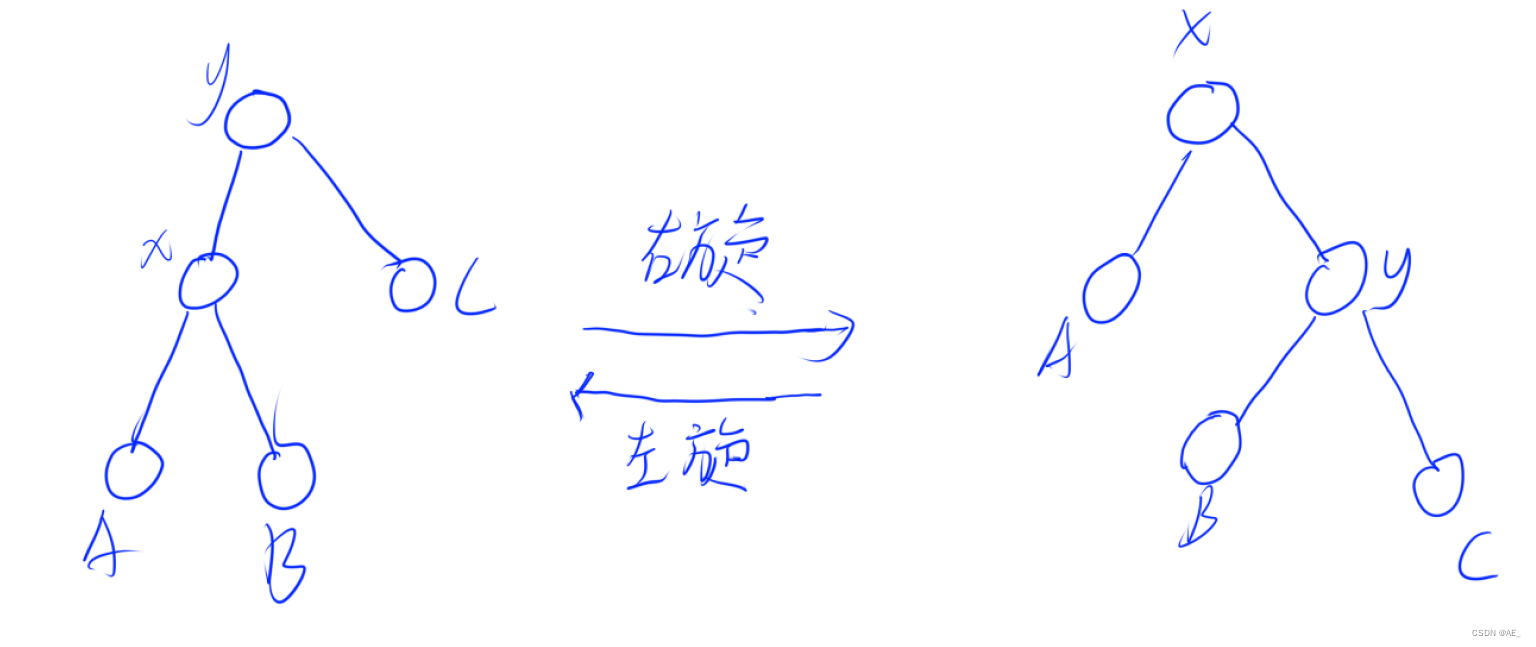
右旋和左旋，目的是為了維護二叉樹的操作，使其盡量平衡。

int n, m;
int o[N];
struct Node { // 節點int l, r; // 左兒子，右兒子int key, val; // 數據值，隨機值（用以維護二叉樹盡量平衡的條件） int cnt, size; // 當前key值的數量，當前子樹的所有節點的cnt值和
} tr[N];
int root, idx; // 根節點，下一個可以分配的節點序號void push_up(int p) { // 與線段樹操作的意義一樣tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt; // 左右子樹的size和加上本身cnt
}int get_node(int key) { // 創建一個節點，返回節點序號tr[++ idx].key = key; // 初始化keytr[idx].val = rand(); // 隨機一個01給valtr[idx].cnt = tr[idx].size = 1; // 數量為1，只有本身return idx; // 返回序號
}void build() { // 建立一個空的二叉樹，只有兩個哨兵，無窮大與無窮小get_node(-INF), get_node(INF);root = 1, tr[1].r = 2; push_up(root);
}void zig(int &p) { // 右旋int q = tr[p].l; // q為根節點左兒子tr[p].l = tr[q].r, tr[q].r = p, p = q; // 對應圖片分析push_up(tr[p].r), push_up(p); // 更新size值
}void zag(int &p) { // 左旋int q = tr[p].r; // q為根節點右兒子tr[p].r = tr[q].l, tr[q].l = p, p = q; // 對應圖片分析push_up(tr[p].l), push_up(p); // 更新size值
}void insert(int &p, int key) { // 插入一個節點keyif(!p) p = get_node(key); // 該key值未出現過，創建一個新的節點，并將序號返回到上一級else if(tr[p].key == key) tr[p].cnt ++; // 出現過，直接cnt數量加一else if(tr[p].key > key) { // 應該插在左兒子insert(tr[p].l, key); // 遞歸左兒子if(tr[tr[p].l].val > tr[p].val) zig(p); // 左兒子val值大于本身，右旋處理} else { // 應該插在右兒子insert(tr[p].r, key); // 遞歸右兒子if(tr[tr[p].r].val > tr[p].val) zag(p); // 右兒子var值大于本身，左旋處理}push_up(p); // 更新size狀態return ;
}void remove(int &p, int key) { // 刪除一個key值節點if(!p) return ; // 沒找到，直接結束if(tr[p].key == key) { // 找到key值節點if(tr[p].cnt > 1) tr[p].cnt --; // 數量不唯一，直接減一即可else if(tr[p].l || tr[p].r) { // 數量唯一且存在兒子if(!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val) {// 右兒子存在或者左兒子var值大于右兒子，右旋處理zig(p);remove(tr[p].r, key);// 右旋之后key值節點交換到當前p節點的右兒子，遍歷右兒子，一直遞歸直到沒有兒子的時候刪除} else {// 應該進行左旋處理zag(p);remove(tr[p].l, key);// 左旋之后key值節點交換到當前p節點的左兒子，遍歷左兒子，一直遞歸直到沒有兒子的時候刪除}} else p = 0; // 數量唯一且沒有兒子，直接刪除即可。} else if(tr[p].key > key) remove(tr[p].l, key); // key值點在左兒子else remove(tr[p].r, key); // key值點在右兒子push_up(p);
}int get_rank_by_key(int p, int key) { // 根據key值找排名if(!p) return 1;  // 沒找到直接return 1，因為洛谷這個題說的是不存在的數的排名為比它的數量加一if(tr[p].key == key) return tr[tr[p].l].size + 1; // 找到key值，返回key值在當前子樹的排名if(tr[p].key > key) return get_rank_by_key(tr[p].l, key);// key在左子樹return get_rank_by_key(tr[p].r, key) + tr[tr[p].l].size + tr[p].cnt; // key在右子樹，因為左子樹以及本身都是比它小的，所以需要加上這些數量，再去遞歸右子樹，計算key值在右子樹的排名
}
int get_key_by_rank(int p, int rank) {  // 找到排名為rank的key值if(!p) return INF; // 沒找到，不存在這個排名的數if(tr[tr[p].l].size >= rank) return get_key_by_rank(tr[p].l, rank); // 在左子樹if(tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key; // 在本身return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt); // 在右子樹，需要減去左子樹以及本身的數量	
}
int get_prev(int p, int key) { // 獲得比key小的最大數if(!p) return -INF; // 沒找到if(tr[p].key >= key) return get_prev(tr[p].l, key); // 在左子樹return max(tr[p].key, get_prev(tr[p].r, key)); // 本身和右子樹都比key小，都有可能，遞歸右子樹與本身進行判斷。
}
int get_next(int p, int key) { // 獲得比key大的最小數if(!p) return INF; // 沒找到if(tr[p].key <= key) return get_next(tr[p].r, key); // 在右子樹return min(tr[p].key, get_next(tr[p].l, key));  // 本身和左子樹都比key大，都有可能，遞歸左子樹與本身進行判斷。
}
inline void sovle() {build();
//	cout << idx << endl;cin >> n;while(n --) {int opt, x;cin >> opt >> x;if(opt == 1) insert(root, x);else if(opt == 2) remove(root, x);else if(opt == 3) cout << get_rank_by_key(root, x) - 1 << endl;else if(opt == 4) cout << get_key_by_rank(root, x + 1) << endl;else if(opt == 5) cout << get_prev(root, x) << endl;else cout << get_next(root, x) << endl;}
}