236. 二叉樹的最近公共祖先

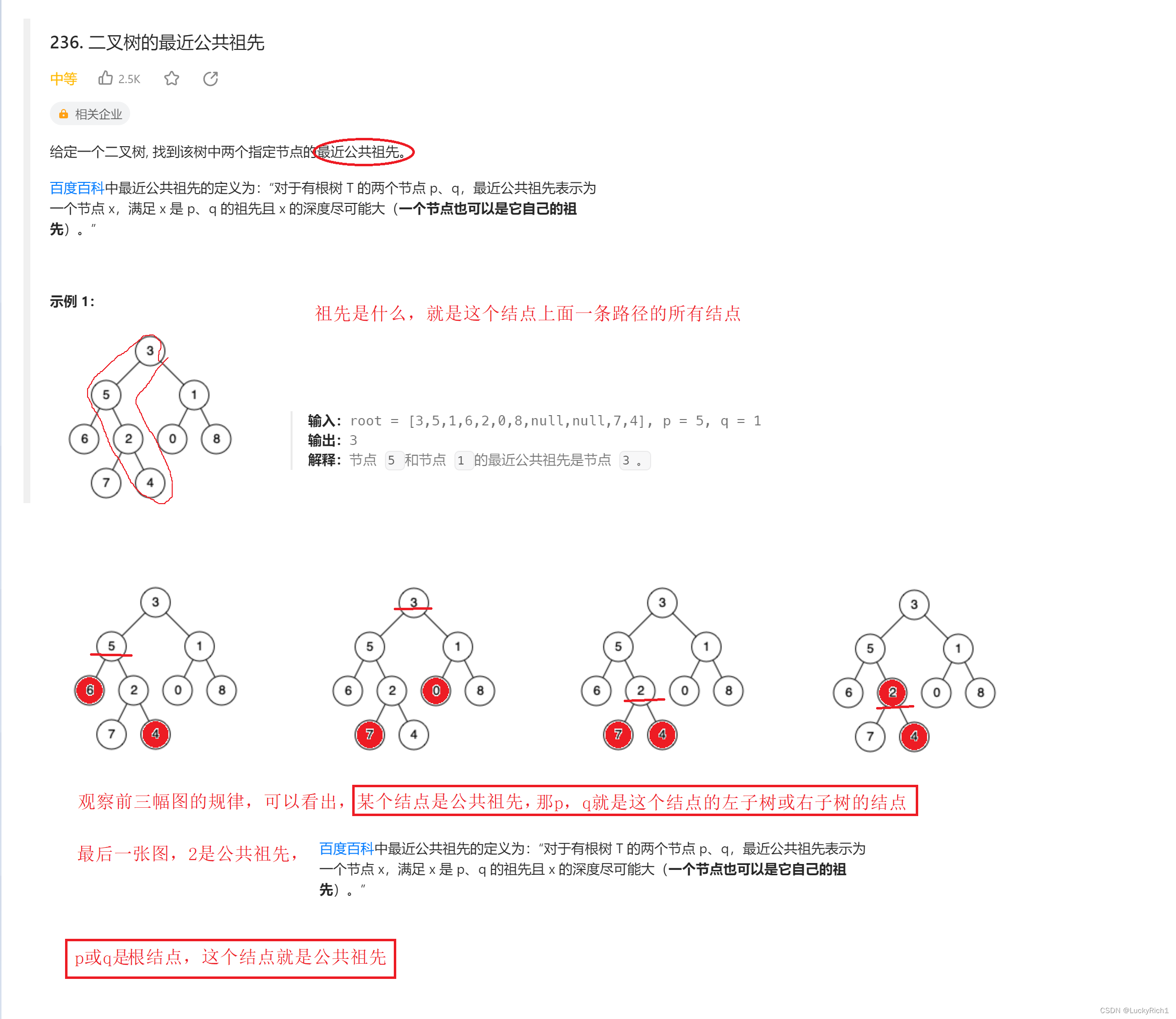
給定一個二叉樹, 找到該樹中兩個指定節點的最近公共祖先。

百度百科中最近公共祖先的定義為：“對于有根樹 T 的兩個節點 p、q，最近公共祖先表示為一個節點 x，滿足 x 是 p、q 的祖先且 x 的深度盡可能大（一個節點也可以是它自己的祖先）。”

示例

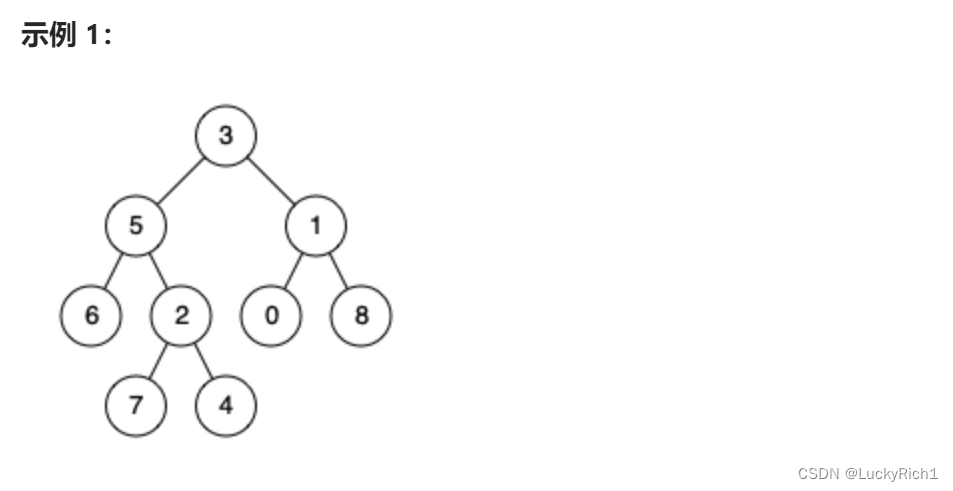
輸入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
輸出：3
解釋：節點 5 和節點 1 的最近公共祖先是節點 3 。

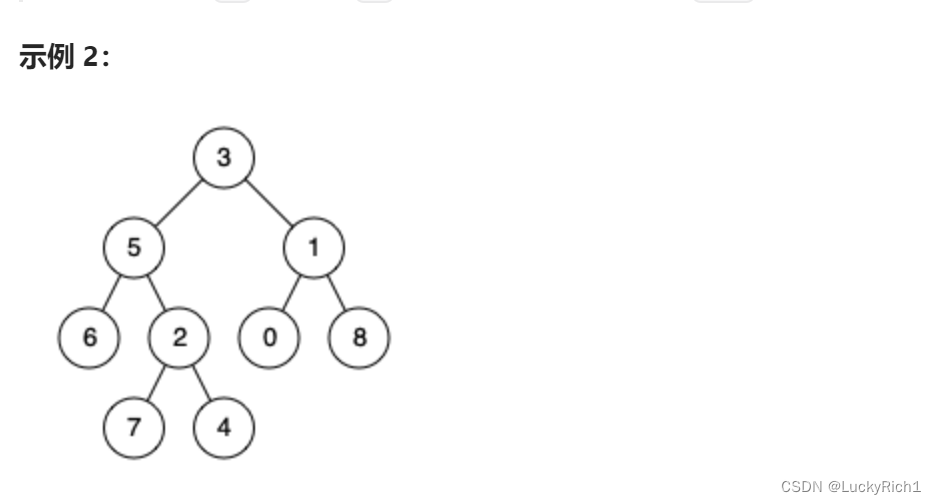
輸入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
輸出：5
解釋：節點 5 和節點 4 的最近公共祖先是節點 5 。因為根據定義最近公共祖先節點可以為節點本身

解題思路及實現

思路一

class Solution {
public://中序遍歷的變形---->Findbool InOrder(TreeNode* root,TreeNode* node){if(root == nullptr)return false;if(root == node)return true;return InOrder(root->left,node) || InOrder(root->right,node);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == nullptr)return nullptr;//p或q是根if(root == p || root == q)return root;//找p，找q, 注意p，q一定在樹中bool pInLeft=InOrder(root->left,p);bool pInRight=!pInLeft;bool qInLeft=InOrder(root->left,q);bool qInRight=!qInLeft;//判斷if((pInLeft && qInRight) || (pInRight && qInLeft))return root;else if(pInLeft && qInLeft)return lowestCommonAncestor(root->left,p,q);elsereturn lowestCommonAncestor(root->right,p,q);}
};

雖然代碼沒問題，但是運行效率太差了。分析一下上面是什么原因導致的。

如果這顆樹是一個二叉搜索樹，我們就不需要去子樹尋找了。
又或者這是一顆三叉樹。

思路二

class Solution {
public://DFS<----->前序遍歷//我們這里是回溯，回溯也是DFS，特點是往回走做一些事情//關于回溯，DFS，前序遍歷不要深究到底是什么有什么區別，其實都是遞歸bool GetPath(TreeNode* root,TreeNode* node,stack<TreeNode*>& st){if(root == nullptr)return false;st.push(root);if(root == node)return true;if(GetPath(root->left,node,st))return true;if(GetPath(root->right,node,st))return true;st.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == nullptr)return nullptr;stack<TreeNode*> pst;stack<TreeNode*> qst;GetPath(root,p,pst);GetPath(root,q,qst);while(pst.size() != qst.size()){if(pst.size() > qst.size())pst.pop();elseqst.pop();}while(pst.top() != qst.top()){pst.pop();qst.pop();}return pst.top();}
};

JZ36 二叉搜索樹與雙向鏈表

JZ36 二叉搜索樹與雙向鏈表這是一道牛客上面的題。

描述

輸入一棵二叉搜索樹，將該二叉搜索樹轉換成一個排序的雙向鏈表。如下圖所示

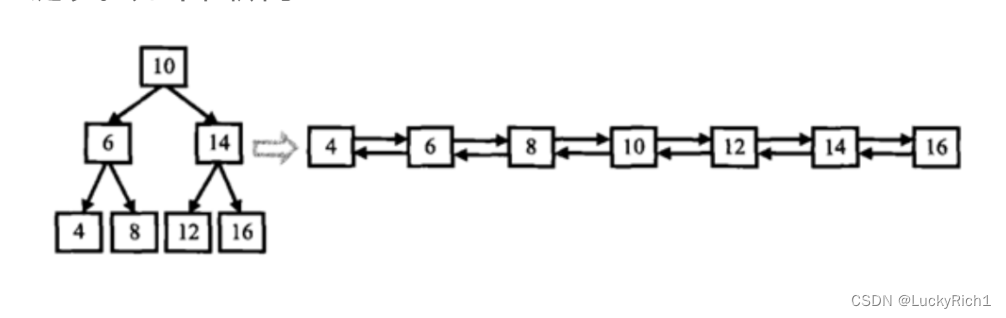
數據范圍：輸入二叉樹的節點數0≤n≤1000，二叉樹中每個節點的值 0≤val≤1000
要求：空間復雜度O(1)（即在原樹上操作），時間復雜度 O(n)

注意:
1.要求不能創建任何新的結點，只能調整樹中結點指針的指向。當轉化完成以后，樹中節點的左指針需要指向前驅，樹中節點的右指針需要指向后繼
2.返回鏈表中的第一個節點的指針
3.函數返回的TreeNode，有左右指針，其實可以看成一個雙向鏈表的數據結構
4.你不用輸出雙向鏈表，程序會根據你的返回值自動打印輸出

解題思路及實現

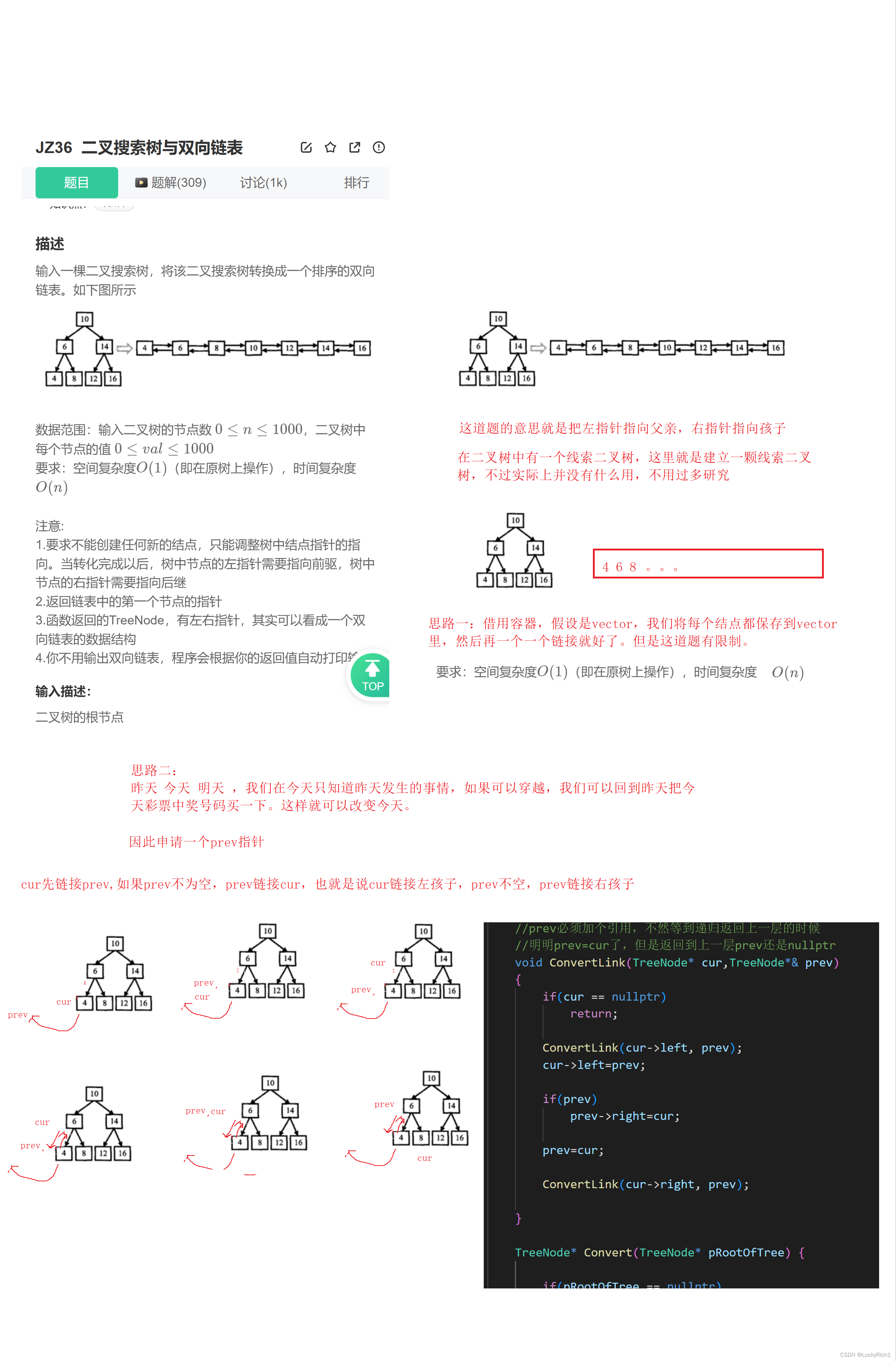
class Solution {
public://prev必須加個引用，不然等到遞歸返回上一層的時候//明明prev=cur了，但是返回到上一層prev還是nullptrvoid ConvertLink(TreeNode* cur,TreeNode*& prev){	if(cur == nullptr)return;ConvertLink(cur->left, prev);cur->left=prev;if(prev)prev->right=cur;prev=cur;ConvertLink(cur->right, prev);}TreeNode* Convert(TreeNode* pRootOfTree) {if(pRootOfTree == nullptr)return nullptr;TreeNode* prev=nullptr;ConvertLink(pRootOfTree,prev);//找鏈表頭，鏈接之后，pRootOfTree還在while(pRootOfTree->left)pRootOfTree=pRootOfTree->left;return pRootOfTree;}
};