1049. 最后一塊石頭的重量 II

題目鏈接：

力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

求解思路：

等于把石頭盡量分成重量相同的兩堆

動規五部曲

1. 確定dp數組及其下標含義：容量為j的背包，最多能裝下的最大重量為dp[j]
2. 確定遞推公式：dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
3. dp數組的初始化：重量不會是負數，全部初始化為0即可
4. 確定遍歷順序：先物品，再背包，且遍歷背包要倒序
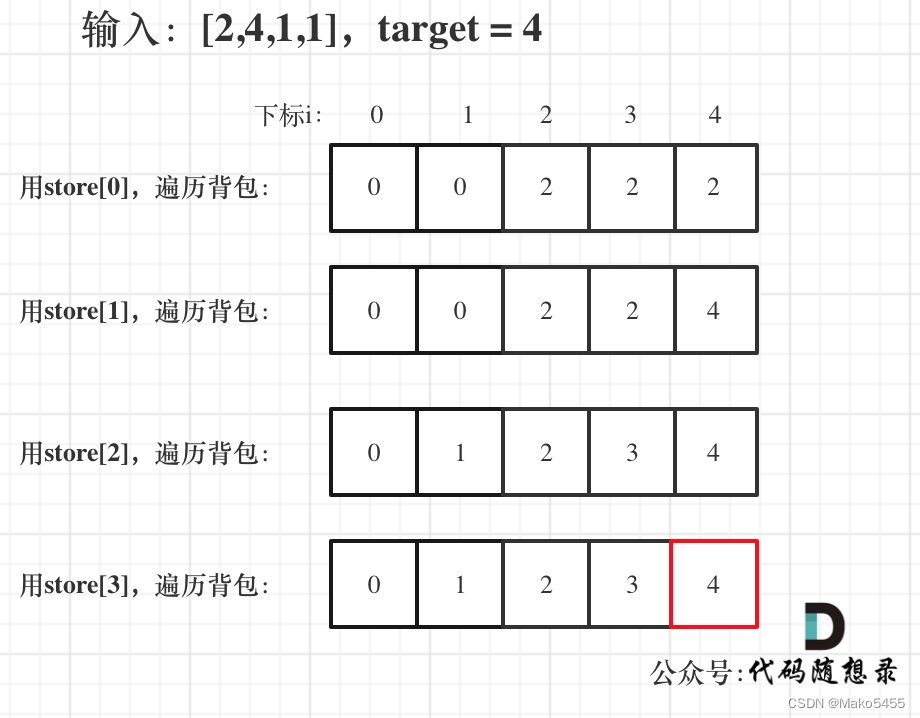
5. 舉例推導dp數組：以[2,4,1,1]為例，如圖。最后相撞后的結果為sum-2*dp[target]

代碼：

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for (int i : stones) sum += i;int target = sum / 2;vector<int> dp(target+1, 0);for (int i = 0; i < stones.size(); i++){for (int j = target; j >= stones[i]; j--){dp[j] = max(dp[j], dp[j-stones[i]] + stones[i]);}}return sum - 2*dp[target];}
};

494. 目標和

題目鏈接：

力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

求解思路：

• 

等于求有多少種不同的組合方式，能組合成和為left的子集（裝滿這個背包有幾種方法）

動規五部曲

1. dp數組及其下標含義：填滿j（包括j）這么大容積的包，有dp[j]種方法
2. 確定遞推公式：dp[j] += dp[j - nums[i]]，舉例說明如下，湊整dp[5]的方法就是把所有的dp[j - nums[i]]累加
   • 已經有一個1（nums[i]） 的話，有 dp[4]種方法 湊成 容量為5的背包。
   • 已經有一個2（nums[i]） 的話，有 dp[3]種方法 湊成 容量為5的背包。
   • 已經有一個3（nums[i]） 的話，有 dp[2]中方法 湊成 容量為5的背包
   • 已經有一個4（nums[i]） 的話，有 dp[1]中方法 湊成 容量為5的背包
   • 已經有一個5 （nums[i]）的話，有 dp[0]中方法 湊成 容量為5的背包
3. 初始化：dp[0] = 1，dp[0]是遞推結果的起源
4. 遍歷順序：先物品，再背包，背包要倒序
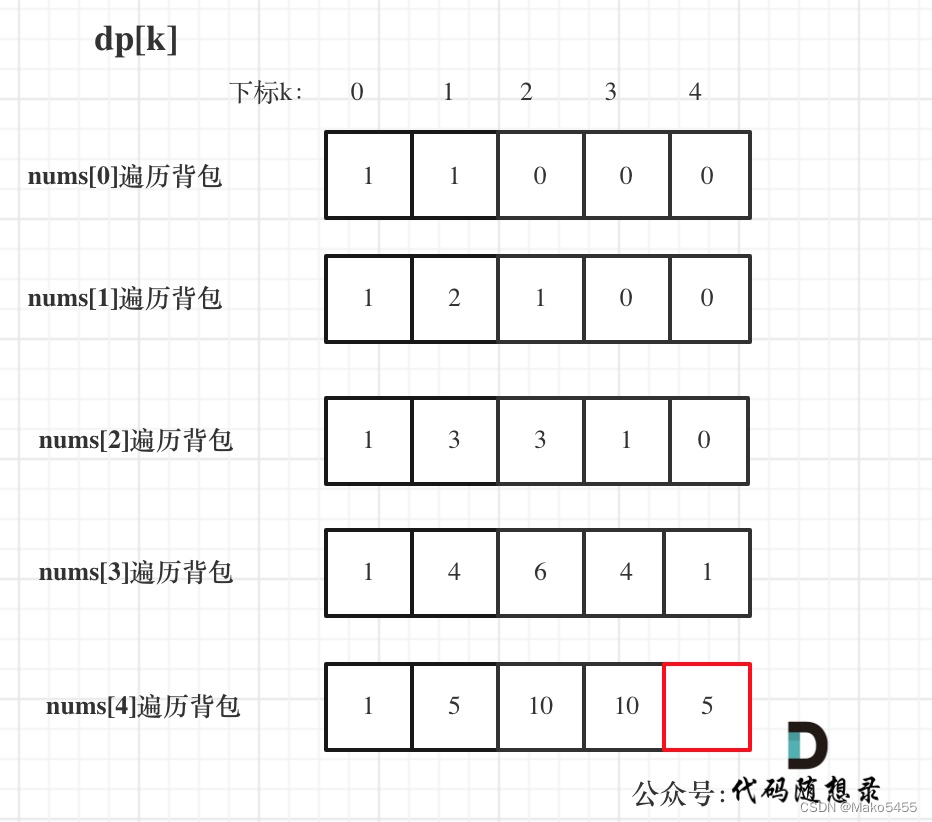
5. 舉例推導dp數組：nums: [1, 1, 1, 1, 1]，target = 3，此時bagSize = 4，如圖

代碼：

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for (int i : nums) sum += i;// 兩種特殊情況if (abs(target) > sum) return 0;if ((target + sum) % 2 == 1) return 0;int bagSize = (target + sum) / 2;// 填滿j（包括j）這么大容積的包，有dp[j]種方法vector<int> dp(bagSize+1, 0);// 初始化dp[0] = 1;for (int i = 0; i < nums.size(); i++){for (int j = bagSize; j >= nums[i]; j--){dp[j] += dp[j-nums[i]];}}return dp[bagSize];}
};

474.一和零

題目鏈接：

力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

求解思路：

動規五部曲

1. 確定dp數組及其下標含義：最多有i個0和j個1的strs的最大子集的大小為dp[i][j]
2. 遞推公式：dp[i][j] 可以由前一個strs里的字符串推導出來，strs里的字符串有zeroNum個0，oneNum個1，則 dp[i][j] = dp[i - zeroNum][j - oneNum] + 1，注意和dp[i][j]本身比較，取較大的值；字符串的zeroNum和oneNum相當于物品的重量（weight[i]），字符串本身的個數相當于物品的價值（value[i]），即01背包問題，不過重量有兩個維度
3. 初始化：物品價值不會為負數，因此全部初始化為0
4. 遍歷順序：先物品，后背包，背包倒序；注意物品是strs里的字符串，背包是題目中的m和n
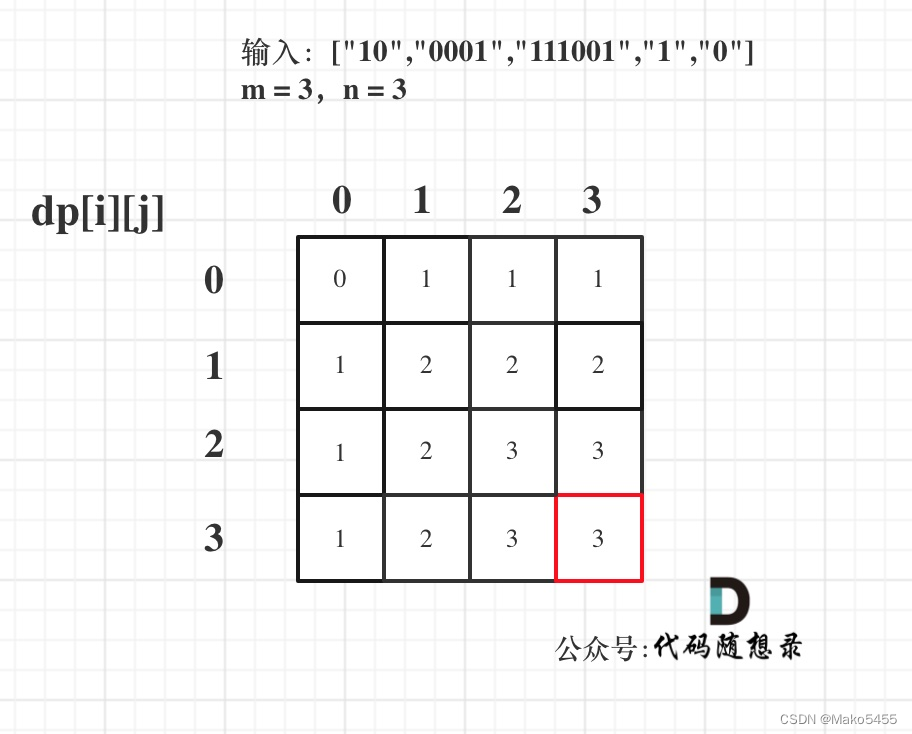
5. 舉例推導：以 ["10","0001","111001","1","0"]，m = 3，n = 3為例，如圖

代碼：

class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {// 初始化vector<vector<int>> dp(m+1, vector<int> (n+1, 0));for (string str : strs){ // 遍歷物品int one = 0, zero = 0;for (char c : str){if (c == '0') zero ++;else one++;}// 遍歷背包（倒序遍歷）for (int i = m; i >= zero; i--){for (int j = n; j >= one; j--){dp[i][j] = max(dp[i][j], dp[i-zero][j-one] + 1);}}}return dp[m][n];}
};